Неопределённый интеграл. Определения.
Неопределённый интеграл для функции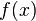 
— это совокупность всех первообразных данной функции.
Если функция 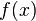определена и непрерывна на промежутке 
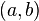и 
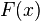— её первообразная, то есть 
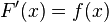при 
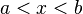, то
,
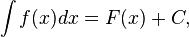
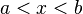где С — произвольная постоянная.
Дадим строгое математическое определение понятия неопределенного интеграла.
Выражение вида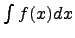 
называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом 
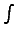всегда присутствует dx.
Определение. Неопределенным интегралом 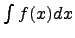называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е. 
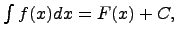или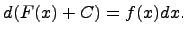 
Функцию 
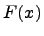называют первообразной функции 
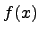. Первообразная функции 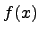определяется с точностью до постоянной величины.
Напомним, что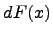 
- дифференциал функции 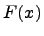и определяется следующим образом:
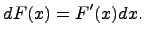
Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.
Например, известно, что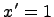 
, тогда получается, что 
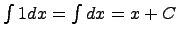, здесь 
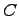- произвольная постоянная.
Свойства неопределённого интеграла.
1. Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то
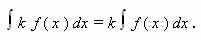
Короче: постоянную можно выносить за знак интеграла.
2. Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то
|
|
|
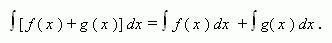
Короче: интеграл суммы равен сумме интегралов.
3. Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:
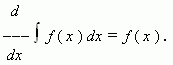
Короче: производная от интеграла равна подынтегральной функции.
4. Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
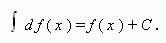
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
Метод подведения функции под знак дифференциала.
Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала:
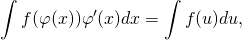
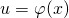
Интегрирование иррациональных выражений.
· Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида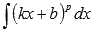 
, где p – рациональная дробь, k и b – действительные коэффициенты.
· Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида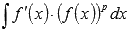 
, где p – рациональная дробь.
· Достаточно часто приходится иметь дело с неопределенными интегралами вида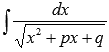 
, где p и q – действительные коэффициенты.
|
|
|
В этом случае выделяем полный квадрат под знаком корня:
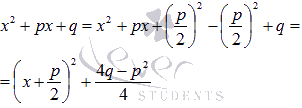
и используем формулу из таблицы неопределенных интегралов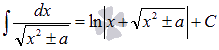 
.
То есть,
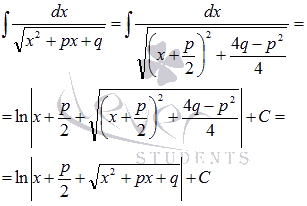
· Аналогично проводится интегрирование иррациональных функций вида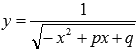 
.
· Нахождение множества первообразных иррациональных функций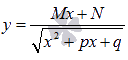 
, где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных.
· Неопределенные интегралы иррациональных функций вида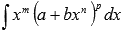 
находятся методом подстановки.
В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:
1. Если p - целое число, то принимают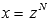 
, где N - общий знаменатель чисел m и n.
2. Если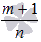 
- целое число, то 
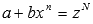, где N - знаменатель числа p.
3. Если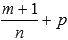 
- целое число, то вводят новую переменную 
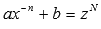, где N - знаменатель числа p.
Дата добавления: 2019-09-13; просмотров: 205; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!