Метод замены переменной и формула интегрирования по частям в определённом интеграле.
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла.
Интегрирование по частям:
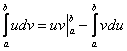
Геометрические приложения определённого интеграла: вычисление площадей плоских фигур.
Пусть функция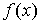 
непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции 
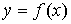, может быть вычислена по формуле:
.
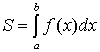Интеграл с переменным верхним пределом.
Пусть на отрезке [ a, b ] задана непрерывная функция f ( x ), тогда для любого x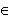 
[ a, b ] существует функция:
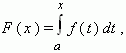
задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
| П р и м е р . | Переменная сила на прямолинейном пути изменяется по закону: f ( x ) = 6x2 + 5 при x 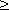 0. По какому закону изменяется работа этой силы ?
|
| Р е ш е н и е. | Работа силы f ( x ) на отрезке [ 0 , x ] прямолинейного пути равна: 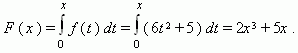 Таким образом, работа изменяется по закону: F ( x ) = 2x 3 + 5x .
|
Из определения интеграла с переменным верхним пределом - функции F(x) и известных свойств интеграла следует, что при x 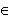[ a, b ]
F' ( x ) = f ( x ) .
Несобственный интеграл.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
· Область интегрирования является бесконечной. Например, является бесконечным промежутком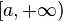 
.
|
|
|
· Функция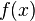 
является неограниченной в окрестности некоторых точек области интегрирования.
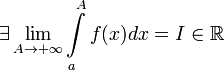
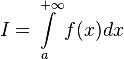
Дифференциальное уравнение. Общее решение д.у.
Дифференциальное уравнение — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).
Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке в дифференциальное уравнение вида
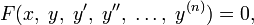
обращает его в тождество.
Если каждое решение дифференциального уравнения представимо в виде:
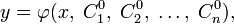
где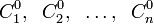 
— конкретные числа, то функция вида
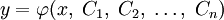
при всех допустимых значениях параметров (произвольных констант)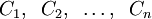 
называется общим решением дифференциального уравнения.
Обыкновенное д.у. и д.у. в частных производных.
Обыкновенные дифференциальные уравнения (ОДУ) — это дифференциальные уравнения для функции от одной переменной.
Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
Дифференциальные уравнения с разделяющимися переменными.
|
|
|
В дифференциальных уравнениях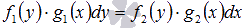 
или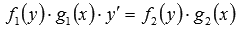 
переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как 
.
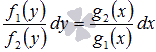Дата добавления: 2019-09-13; просмотров: 209; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!