Уравнение касательной к графику функции в данной точке.
Пусть дана функция f, которая в некоторой точке x0 имеет конечнуюпроизводную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.
Всякая невертикальная прямая задается уравнением вида y = kx + b,где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Пример: Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
Теоремы Ферма, Ролля, Лагранжа, Коши (формулировки и геометрический смысл).
Теорема Ферма. (О равенстве нулю производной)
Пусть функция 
удовлетворяет следующим условиям:
· она дифференцируема на интервале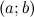 
;
|
|
|
· достигает наибольшего или наименьшего значения в точке 
.
Тогда производная в этой точке равна нулю, то есть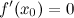 
.
Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)
Пусть функция
· непрерывна на отрезке 
;
· дифференцируема на интервале ;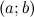
· на концах отрезка принимает равные значения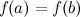 
.
Тогда на интервале 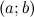найдется, по крайней мере, одна точка 
, в которой .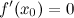
Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Следствие.
Если 
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
Теорема Лагранжа. (О конечных приращениях)
Пусть функция
· непрерывна на отрезке ;
· дифференцируема на интервале .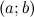
Тогда на интервале 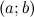найдется по крайней мере одна точка , такая, что
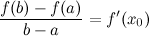
Теорема Ролля есть частный случай теоремы Лагранжа, когда .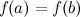
|
|
|
Следствие. (Геометрический смысл теоремы Лагранжа)
На кривой между точками 
и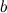 
найдется точка 
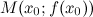, такая, что через эту точку можно провести касательную, параллельную хорде 
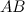(рис. 1).
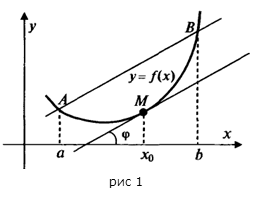
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
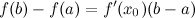
Теорема Коши. (Об отношении конечных приращений двух функций)
Если функции и 
:
· непрерывны на отрезке ;
· дифференцируемы на интервале ;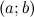
· производная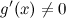 
на интервале ,
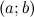тогда на этом интервале найдется по крайней мере одна точка , такая, что
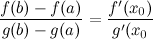
Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.
Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.
Дата добавления: 2019-09-13; просмотров: 192; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!