Элементарные функции, их свойства.
Множество. Действия над множествами.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п., например:
N - {1,2,3,...,n} Множество всех натуральных чисел.
Z - {0, ±1, ±2, ±3,...} Множество целых чисел.
Q - Множество рациональных чисел.
R - Множество всех вещественных чисел
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то А/В = {1,2}.
Функция. Определение. Способы задания. Область определения. Множество значений. Примеры.
Зависимость одной переменной от другой называется функциональной зависимостью.
Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.
Обозначение: 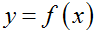
Переменную x называют независимой переменной или аргументом, а переменную y - зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.
Способы задания функции:
1) Функция может быть задана аналитически в виде формулы. Например, 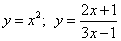
2) Функция может быть задана таблицей из множества пар (x; y).
3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.
Все возможные значения, которые принимает x, образуют область определения функции; все возможные значения, которые принимает y, образуют множество значений функции.

Четность и нечетность функции. Монотонность. Ограниченность. Периодичность. Примеры.
Четные и нечетные функции
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "взбираться" вверх по графику.
Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "скатываться" вниз по графику.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Ограниченная функция
Пусть функция (одного или многих переменных) определена на множестве D. Если множество ее значений ограничено, когда аргумент (аргументы) пробегают все множество D, функция называется ограниченной. Соответственно, если множество значений функции ограничено сверху (снизу), то функция также называется ограниченной сверху (снизу).
Периодическая функция
Функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
Говоря более формально, функция называется периодической с периодом, 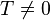 , если для каждой точки
, если для каждой точки 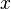 из её области определения точки
из её области определения точки 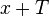 и
и 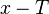 также принадлежат её области определения, и для них выполняется равенство
также принадлежат её области определения, и для них выполняется равенство 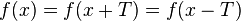 .
.
Исходя из определения, для периодической функции справедливо также равенство: 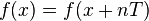 , где
, где 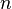 — любое целое число.
— любое целое число.
Все тригонометрические функции являются периодическими.
Элементарные функции, их свойства.
Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
· Постоянная функция (константа). 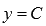
· Корень n-ой степени. 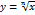
· Степенная функция. 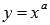
· Показательная функция. 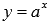
· Логарифмическая функция. 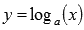
· Тригонометрические функции. 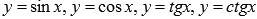
· Обратные тригонометрические функции (аркфункции). 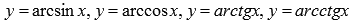
Дата добавления: 2019-09-13; просмотров: 255; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
