Правило Лопиталя раскрытия неопределённостей.
Теорема Лопиталя (также правило Бернулли — Лопиталя) — метод нахождения пределов функций, раскрывающий неопределённости вида 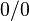 и
и 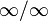 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя:
Если:
1. 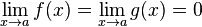 или
или 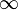 ;
;
2. 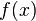 и
и 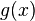 дифференцируемы в окрестности
дифференцируемы в окрестности 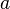 ;
;
3. 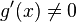 в окрестности
в окрестности 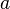 ;
;
4. существует 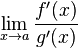 ,
,
то существует 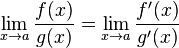 .
.
Пределы также могут быть односторонними.
Достаточные условия возрастания и убывания функции.
Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f'(x)>0), то на этом промежутке функция возрастает.
Если производная некоторой непрерывной функции f(x) на некотором промежутке отрицательна (f'(x)<0), то на этом промежутке функция убывает.
Эти условия являются достаточными условиями возрастания (убывания функции).
Экстремумы функции. Необходимое условие экстремума.
Точка x0 называется точкой максимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка 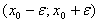 , выполняется неравенство
, выполняется неравенство 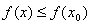 . Иными словами, значение функции f(x0) самое большое в некоторой окрестности точки x0.
. Иными словами, значение функции f(x0) самое большое в некоторой окрестности точки x0.
Точка x0 называется точкой минимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка 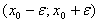 , выполняется неравенство
, выполняется неравенство 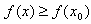 . Иными словами значение функции f(x0) самое маленькое в некоторой окрестности точки x0.
. Иными словами значение функции f(x0) самое маленькое в некоторой окрестности точки x0.
|
|
|
Точки максимума или минимума называются точками экстремума.
Теорема Ферма: Если x0 - точка экстремума непрерывной функции f(x), то f'(x0)=0.
Геометрически это выглядит так: в точке экстремума касательная параллельна оси ОХ и, поэтому угол наклона равен 0.
Это условие является необходимым, но не достаточным условием экстремума.
Достаточные условия экстремума функции.
· Пусть функция 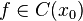 непрерывна в
непрерывна в 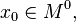 и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные 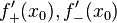 . Тогда при условии
. Тогда при условии
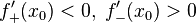
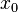 является точкой строгого локального максимума. А если
является точкой строгого локального максимума. А если
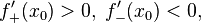
то 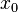 является точкой строгого локального минимума.
является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке 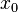 .
.
· Пусть функция 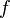 непрерывна и дважды дифференцируема в точке
непрерывна и дважды дифференцируема в точке 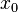 . Тогда при условии
. Тогда при условии
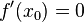 и
и 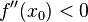
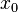 является точкой локального максимума. А если
является точкой локального максимума. А если
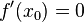 и
и 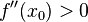
то 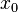 является точкой локального минимума.
является точкой локального минимума.
· Пусть функция 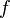 дифференцируема
дифференцируема 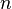 раз в точке
раз в точке 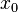 и
и 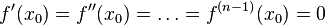 , а
, а 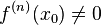 .
.
Если 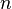 чётно и
чётно и 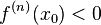 , то
, то 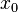 — точка локального максимума. Если
— точка локального максимума. Если 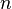 чётно и
чётно и 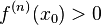 , то
, то 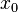 — точка локального минимума. Если
— точка локального минимума. Если 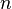 нечётно, то экстремума нет.
нечётно, то экстремума нет.
Выпуклость функции. Точки перегиба.
Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x ) в любой точке ( x0, f ( x0 ) ), x0 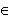 ( a, b ).
( a, b ).
|
|
|
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f (x ) в любой точке ( x0, f ( x0 ) ), x0 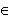 ( a, b ).
( a, b ).
Дата добавления: 2019-09-13; просмотров: 171; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
