ТЕМА 4. МЕТОДИКА ИЗУЧЕНИЯ ТОЖДЕСТВЕННЫХ
ПРЕОБРАЗОВАНИЙ
4.1. Роль и место тождественных преобразований в школьном курсе математики. Пропедевтика тождественных преобразований в 5 - 6 классах
Тождественные преобразования представляют собой одну из главных линий школьного курса математики. На их основе формируются представления об аналитических методах математики. Как правило, решение каждой математической задачи аналитическим методом предполагает выполнение некоторых тождественных преобразований.
Тождественные преобразования не являются какой-либо отдельной темой школьного курса математики, они изучаются на протяжении всего курса арифметики, алгебры и начал анализа. Без них не обходятся и на уроках геометрии.
Изучение темы имеет как самостоятельное, так и прикладное значение. Материал линии связан
- с обобщением операций над числами;
- проведением вычислений в общем виде;
- обучением использования буквенной символики в математике и ее приложениях.
Существует два подхода к изучению линии тождеств: алгебраический и функциональный.
Алгебраический подход. Больше внимания уделяется букве и операциям над буквенными выражениями. На выражение смотрят формально, не задумываясь над тем, что скрывается под буквами. Все преобразования опираются на правила действий и свойства действий.
Функциональный подход. Входящие в выражения буквы понимаются как переменные, а тождественные преобразования опираются на условие равенства функций (равенство значений функций при всех допустимых значениях переменной).
|
|
|
Понятие о тождественных преобразованиях закладывается в сознание ученика уже в 5 классе, хотя, согласно программе, термины «тождество» и «тождественное преобразование» еще не введены. В 5-м классе даются задания, в которых рассматриваются некоторые преобразования числовых выражений и выражений, содержащих переменные; тождественные преобразования, выполняемые на основе свойств арифметических действий. Учащиеся знакомятся с первыми основными тождествами (например, ab = ba, a(b+c) = ab + ас и др.), а затем применяют их при решении следующих видов упражнений:
1.Найти значение выражения: 977*43+43*23 = 43*(977+23)
2. При каких значениях переменной истинны равенства:
3(х+5) = Зх +15; (7+х)5 = 7*5+х*5?
3.Выполнить действия 129*70 = (130-1)*70 = 9100 - 70
4.Сократить дробь 9/129 = 9/3*43 = 3/43.
Используя такого рода упражнения, мы не просто подготавливаем учащихся к введению понятия тождественного преобразования, но и готовим их к осознанию целесообразности тех или иных преобразований.
В 6-м классе дается понятие коэффициента, учащиеся знакомятся с выражениями вида: 2а, -ab, -Заb, то есть фактически постигают понятие одночлена, хотя термин «одночлен» не вводится. Приведение подобных слагаемых рассматривается как пример применения распределительного свойства к сумме произведений с одинаковыми буквенными множителями: За + 4b + 2а = а(3+2) + 4b = 5а + 4b.
|
|
|
Определения понятий «тождество» и
«тождественное преобразование»
Первое определение тождества дается в 7-м классе.
Определение Равенство, верное при любых значениях переменной, называется тождеством.
Данное определение компактно и хорошо, когда учащиеся работают с целыми рациональными выражениями. Так равенства вида а2 /а = а или 
не подходят под это определение, поэтому его необходимо уточнить, и в 8-м классе в теме «Рациональные дроби» дается уже другое определение: Равенство, верное при всех допустимых значениях, входящих в него переменных.
Наиболее общим является следующее определение: Равенство, верное при любых значениях переменных, принадлежащих некоторому множеству , называется тождеством на этом множестве.
Данное определение раскрывает суть тождества с теоретико-функциональной точки зрения.
Например, (а+в)2 = а2+2ав+в2 - тождество на R;
- тождество на R+;
- тождество при х>0
|
|
|
Некоторые тождества выбираются как основные, с их помощью доказываются остальные тождества и рассматриваются свойства операций, истинность которых принимается в качестве аксиом (коммутативность, ассоциативность, дистрибутивность, существование противоположного элемента и др.)
Различают понятия:
Тождества-равенства (формулы сокращенного умножения, свойства степени с натуральным показателем и др.)
Тождества-действия (вынесение общего множителя за скобку, приведение подобных слагаемых и др.) или тождественные преобразования.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием.
К тождественным преобразованиям можно отнести, например, приведение подобных слагаемых, разложение на множители, сокращение дробей и так далее.
Процесс формирования навыков
Тождественных преобразований
Содержание линии тождественных преобразований выделяется в настоящее время достаточно четко. В нее входят: изучение тождеств в числовой системе, их применение к упрощению выражений и решению уравнений, изучение тождеств в классе элементарных функций. Организация изучения отдельных тождеств предполагает использование специальных циклов заданий. Цикл заданий на материале конкретной темы характеризуется соединением в последовательность упражнений нескольких аспектов изучения и приемов расположения материала. Применительно к тождественным преобразованиям представление о цикле может быть дано следующим образом. Задания связаны с изучением одного тождества, вокруг которого группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла, наряду с исполнительными, входят задания, требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Учитывается специфика тождества.
|
|
|
Задания в цикле разбиты на две группы.
I группа. Задания, выполняемые при первоначальном знакомстве с тождеством. Это материал для нескольких идущих подряд уроков. Это этап усвоения тождества, запоминания его словесной формулировки, выработки навыка его применения в хорошо видной ситуации.
II группа связывает изучаемое тождество с различными его применениями. Это этап углубленного понимания тождества за счет рассмотрения его в разнообразных ситуациях в сочетании с использованием материала, относящегося к другим темам школьного курса.
Рассмотрим систему упражнений для усвоения тождества
а2-в2 = (а-в) (а+в)
| Задания | Методические указания |
| 1 группа 1.Представить в виде произведения: a) m2-n2 в) с2 - 52 с) 196- к2 | Формируется структура изучаемого тождества, уточняются связи между его словесным выражением и символической формой. Идет работа не только с буквенными, но и буквенно-числовыми выражениями. |
| 2.Проверить справедливость равенства: (102-1)(102+1) = 104-1 | Задание направлено на формирование навыка двустороннего преобразования |
| 3. Раскрыть скобки в выражении: (4ху + 5х2)(4ху - 5х2) | Идет отработка применения тождества |
| 4.Вычислить: 252-242; 49*51 | Эта группа упражнений углубляет представление об операции подстановки и развивает навыки ее применения |
| 5.Разложить на множители: х4-у4; 16(ав)2-(а-в)2 | Изучаемое тождество применяется дважды. |
| 6.Упростить: (а+в)2 - (а-в)2 | Переосмысление изучаемого тождества в терминах отношений между компонентами арифметических действий. |
2 группа
1.Разложить на множители: х2-5
2.Исключить иррациональность в знаменателе дроби:
3.Доказать, что если к - нечетное число, то к - 1
кратно 4
4.Функция задана выражением
х2 + 2| х | + 1
f (х) =------------------
х2 - 1
Упростить, раскрыв знак модуля.
| Идет привлечение новой операции - извлечение корня. Задания предполагают наличие уже сформированных навыков использования изучаемого тождества для разности квадратов. Цель предлагаемых заданий - углубить понимание тождества за счет рассмотрения разнообразных приложений его в различных ситуациях, в сочетании с использованием материала, относящегося к другим темам курса математики. |
| 5. Решить уравнение: х3 - 4х = 15 (*) | (*) <=> х3 - 9х = 15 - 5х <=> х(х-3)(х+3) = 5(3-х) <=> х=3. или х(х+3) = -5. Но уравнение х(х+3) = -5 действительных корней не имеет, поэтому х =3 - единственный корень уравнения. Здесь использование тождества для разности квадратов составляет лишь часть решения уравнения, являясь ведущей идеей проведения преобразований. |
В курсе основной школы рассматриваются алгебраические выражения, то есть выражения, которые не содержат над переменными никаких действий, кроме арифметических операций, операций извлечения корня и возведения в степень с рациональным показателем (см. табл. 1). Новому преобразованию начинаем обучать, если у учащихся уже сформирована база для их выполнения (см. табл. 2).
Формирование навыков тождественных преобразований более быстро протекает, если учитель добивается от учащегося устного выполнения некоторых преобразований не только при устном счете, но и в процессе решения задач.
Полезно также иметь в виду, что всякий раз, когда возникает необходимость в тождественном преобразовании, мы имеем дело с выражением, область определения которого задана. При выполнении преобразования она может расширяться или сужаться.
Пример
1. 
- расширилась
2. 
- сузилась
Этого можно избежать, если осуществлять преобразования на области определения исходного выражения:
Доказательство тождеств
В процессе обучения у учащихся должны быть сформированы навыки доказательства тождеств следующими способами.
Если надо доказать, что А=В, то можно
1. доказать, что А - В = О,
2.доказать, что А/В = 1,
3. преобразовать А к виду В,
4. преобразовать В к виду А,
5. преобразовать А и В к одному виду С.
В качестве опоры, на которой строятся доказательства тождеств, используются свойства арифметических операций. Иногда в доказательстве привлекаются геометрические понятия и методы. Геометрические доказательства не только поучительны и наглядны, но и способствуют усилению межпредметных связей.
Доказательства тождеств можно разделить на три типа в зависимости от того, насколько они удовлетворяют требованиям строгости:
а) Не полностью строгие рассуждения, требующие использования метода математической индукции для придания им полной строгости. Эти доказательства применяются для вывода правила действий с многочленами, свойств степеней с натуральными показателями. Например,
акар = (а ·а·······а) (а ·а········а) = а ·а········а = ак+р
к раз р раз к+р раз
б) Полностью строгие рассуждения, опирающиеся на основные свойства арифметических действий и не использующие других свойств числовой системы. Основная область применения таких доказательств - тождества сокращенного умножения. Многие из утверждений, выражаемых формулами сокращенного умножжения, допускают наглядно-геометрическую иллюстрацию.
Пример Для тождества 
учитель может предложить следующую иллюстрацию:
| a | b | c | |
| a | a2 | ab | ac |
| b | ab | b2 | bc |
| c | ac | bc | c2 |
в) Полностью строгие рассуждения, использующие условия разрешимости уравнений вида Ψ(х) = а, где Ψ - изучаемая элементарная функция. Такие доказательства характерны для вывода свойств степени с рациональным показателем и логарифмической функции. Например, при доказательстве свойства арифметического корня
(1)
будем опираться на переформулировку определения арифметического квадратного корня: для неотрицательных чисел х и у равенства у = 
и
у2 = х равносильны, поэтому (1) равносильно (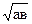 
)2 = ( 
)2 (2). Откуда следует, а в = ( 
)2(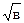 
)2 = а в.
Прием доказательства, который здесь использовался, применяется довольно редко, тем не менее, необходимо подчеркнуть, что основная идея доказательства состоит в сопоставлении двух операций (или функций) - прямой и обратной к ней, что найдет применение уже в старшей школе.
Технологическая цепочка формирования алгоритмов и приемов
тождественных преобразований выражений в основной школе
| Линия | Алгоритм и приемы вычислений |
| Целые выражения Виды целых выражений (одночлен, многочлен), их степень, стандартный вид, частные случаи, формулы сокращенного умножения. Действия с целыми выражениями: разложение многочлена на множители; выделение полного квадрата в трехчлене. | 1. Алгоритмы выполнения основных действий с целыми выражениями. 2. Приемы разложения многочлена на множители. 3. Специальный прием выделения полного квадрата в трехчлене. 4. Обобщенный прием упрощения целого выражения. 5. Приемы доказательства тождества. |
| Рациональные выражения Основное свойство дробного выражения и следствия из него. Сокращение дробных выражений. Действия с рациональными выражениями. | 6. Приемы записи преобразований рациональных выражений. 7. Приемы использования аналогии с действиями над рациональными числами в общих и частных случаях. 8. Обобщение приемов 4 и 5. |
| Иррациональные выражения Основное свойство корня, простейшие преобразования корней. Действия с корнями, возведение выражения в степень с дробным показателем. | 9. Специальные приемы основных преобразований арифметических корней. 10.Приемы преобразования выражений со степенями с рациональным показателем. 11.Прием доказательства неравенств. 12.Обобщение приемов 2, 4, 5 и 11. |
Задание к лекции
Проанализировав школьные учебники составить таблицу тождественных равенств с указанием множества, на котором оно выполняется.
Пример 
, М1 – те х , для которых имеет смысл f(x).
Дата добавления: 2019-09-02; просмотров: 9763; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!