ТЕМА 7. МЕТОДИКА ИЗУЧЕНИЯ ФУНКЦИЙ

В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ

Функции, их свойства и графики составляют стержень школьного курса математики.

«Понятие «функция» как ни одно другое воплощает в себе диалектические черты математического мышления. Именно оно приучает мыслить величины в их живой изменчивости, взаимосвязи, а не в отрыве друг от друга.»[9]

Тезис Б.В. Гнеденко том, что «математика изучает не само явление, а лишь его математическую модель» наполняется конкретным содержанием при изучении 4 типов основных моделей реальной действительности:

- линейная функция – модель равномерных процессов;

- квадратичная функция – модель равноускоренных процессов;

- тригонометрическая функция – модель периодических процессов;

- показательная функция – модель органического роста и убывания.

Слово «функция» происходит от латинского «function» - исполнение служебной обязанности.

Значительная часть материала функциональной линии относится к изучению класса функций, получивших название элементарных[10].

 

Определение функции в школьных учебниках

АЛГЕБРА-7 (С.А. Теляковский) В предыдущих изданиях предлагалось следующие определение функции:

«Зависимость переменной у от переменной х называется функцией, если каждому значению переменной х соответствует единственная переменная у.»

В издании 2000 г. объяснительный текст начинается с примеров описания различных ситуаций, знакомых учащимся:

1. Площадь квадрата зависит от длины его стороны S=a², где а – переменная, значение которой выбирается.

2. При движении со скоростью 50 км/ч за время t автомобиль пройдет путь S= 50t км/ч.

3. Приводится график изменения температуры воздуха в течение суток.

4. Приводится таблица зависимости стоимости проезда на железнодорожном транспорте от номера зоны проезда.

Делается вывод, что в приведенных примерах описывается следующая ситуация: каждому значению независимой переменной соответствует единственное значение зависимой переменной. «Такую зависимость одной переменной от другой называют функциональной или функцией.»[11]

АЛГЕБРА - 7 (Ш.А. Алимов). Приводится задача о движении поезда Москва – Санкт–Петербург, который движется со скоростью 120 км/ч. «За время t поезд пройдет путь равный S = 120 t. Путь S и время t изменяются, поэтому их называют переменными. Значение S зависит от значения t. Поэтому t – независимая, а S – зависимая переменная или функция.

Зависимость переменной S от переменной t называют функциональной.Пишут S ( t), чтобы подчеркнуть, что S зависит отt .»

Далее рассматривается та же задача, но вычисляется время t = s/120. «В данном случае t зависит от S, то есть возникает зависимость t ( S). Каждая из формул устанавливает правило вычисления по заданному значению независимой переменной значения зависимой переменной, то есть функция – это правило».

АЛГЕБРА – 8 (С.М. Никольский). Объяснение начинается в несколько академическом стиле с примера:

«Для любого куба V = a³  (a>0). Любому значению длины ребра а, в силу закона выполняемого равенства, соответствует определенное значение V . Говорят, что V есть функция а, которая определена на множестве положительных чисел».

Затем рассматривается задача о движении тела «со скоростью v = 80км/ч. S = 80 t , ( t 0). S –функция от t , определенная на множестве неотрицательных чисел.»

Далее вводится определение:

«Пусть М – есть некоторое множество чисел, любому числу х из множества М в силу некоторого выше определенного закона приведено в соответствие одно число у. Тогда говорят, что у есть функция от х, которая определена на множестве М, при этом х называется независимой переменной или аргументом, у – зависимой переменной, или функцией от х.

Множество М называется областью определения функции.

Чтобы указать, что у есть функция от х, пишут у = f ( x ), где f характеризует то правило, по которому получается значение у, соответствующее х».

МАТЕМАТИКА – 8 (Г.В. Дорофеев). Введение понятия начинается с чтения графиков некоторых реальных ситуаций. Затем вводится определение: «Переменную у называют функцией переменной х, если каждому значению х из некоторого числового множества соответствует одно определенное значение у».

«Таким образом, функция – это переменная, однако, в математике этот термин традиционно употребляется в более широком смысле. Функцией часто называют не только одну из двух переменных, но и саму зависимость между ними, а также правило, по которому устанавливается соответствие между переменными. Правило часто обозначается символом f, и вводится обозначение у = f ( x )».

АЛГЕБРА – 9 (А.Г. Мордкович). «Если дано числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(x), где х Х.

Подчеркнем, что нельзя говорить о функции без указания области ее определения».

Замечание. Определение функции вводятся в 7, 8, 9 классах, но по–разному.

7.2. Проблемы, возникающие при изучении темы «Функция»

1. Определение функциональной зависимости

Необходимо акцентировать внимание учащихся на роли букв у, х, f , то есть на том, что буква f в отличие от букв у и х обозначает не переменную величину, а то правило (закон), по которому устанавливается соответствие между у и х. Символ f называют характеристикой функции. Если функция задана формулой у = х² – 3х, то роль f играет следующие утверждение:

«Чтобы получить значение у, зная значение х, нужно из квадрата числа х вычесть утроенное это число».

Целесообразно рассмотреть следующие упражнения:

1.Объясните смысл букв у , х, f в записи: у = f ( x ).

2.у = 2х³. Каков закон образования этой функции? Что в ее записи играет роль знака f ?

3.Укажите законы образования функций: у = 5х, у = 3, у = .

2. Способы задания функции

а) Зачастую функция отождествляется учащимися с формулой, которая описывает ее. Следует отметить, что

- не всякая формула задает функцию (например, у = log₂x – log₂(-x)…);

- некоторые функции невозможно задать формулой (например, функцию Дирихле):

у =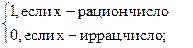

  - функция может быть задана сразу несколькими формулами:

  , 1 х 2

у = 1 + х, 2<x<10,

          sinx, x 10.

Учащиеся должны усвоить, что формула – это не сама функция, а лишь один из способов ее задания.

в) В учебнике понятие графика функции вводится после повторения координатной плоскости (С.М. Никольский, Г.В. Дорофеев, А.Г. Мордкович). В учебниках Ш.А. Алимова, С.А. Теляковского – сразу после определения функции.

Определение. Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а координаты – соответствующим значениям функции.

Для правильного усвоения учащимися понятий «функция» и «график функции» полезно рассмотреть так называемые кусочные функции, которые в большинстве случаев являются моделями реальных процессов и способствуют преодолению заблуждения учеников, отождествляющих функцию с ее аналитическим выражением.

Некоторые методические указания по изучению темы

«График функции» (Алгебра – 8 Г.В. Дорофеев)

 5.1 Чтение графиков

  С графиками реальных процессов учащиеся работали в 6 классе, поэтому рассматриваемый в параграфе материал в какой–то степени им известен. Но учеников необходимо познакомить с некоторыми новыми графическими характеристиками – сравнением скоростей протекающих процессов и вычислением этих скоростей, определением максимальных и минимальных значений. Больше внимания необходимо уделить самостоятельному построению учащимися графиков.

В объяснительном тексте представлены три примера. Первый – график роста ребенка – позволяет повторить известный из курса 6 класса материал и продемонстрировать учащимся, как на графике отражается изменение скорости роста. Разбирая этот пример, учителю следует обратить внимание учащихся на разные масштабы по осям.

Два других примера демонстрируют возможность представления на одном чертеже сразу нескольких графиков: изменения веса двух детей, бега трех спортсменов.

Необходимо научить школьников извлекать из графиков самую разнообразную информацию, причем не только количественную.

5.3 График функции

Теоретический материал разделен на два фрагмента.

Первый – это введение новых обозначений для числовых промежутков, которые уже рассматривались в 6 классе и задавались с помощью неравенств: отрезок, луч, интервал.

Второй фрагмент – это собственно материал, связанный с графиками функций. Рассматриваемые две задачи являются центральными на данном этапе изучения материала.

Первая – это нахождение с помощью графика значения функции, соответствующего заданному значению аргумента, а также значений аргумента, которым соответствует данное значение функции.

Вторая – построение графиков функций по точкам. Пример, рассматриваемый в заключении, помогает учащимся уяснить, что не всякое уравнение или график задают функцию.

В ходе выполнения упражнений школьники учатся по–разному описывать графическую ситуацию, используя геометрический, алгебраический, функциональный языки.

с) Учащиеся зачастую не допускают мысли, что одна и та же функция может быть задана различными способами: аналитически (формулой), графически (когда график строит прибор или человек по наблюдениям), таблично (важно, чтобы были перечислены все соответствующие пары чисел), описательно (например, в учебнике А.Г. Мордковича на это обращается специальное внимание при задании функции у = , а в учебнике С.А. Теляковского – только в задачном материале: «Каждому натуральному числу n ставится в соответствие остаток r от деления этого числа на 4. Найдите область определения и множество значений этих функций.»)

Разные способы задания функции обладают своими недостатками и преимуществами. Так, если функция задана аналитически, удобно находить ее значение при любом значении аргумента из области определения, исследовать ее свойства, но при этом отсутствует наглядность, которую дает графический способ. Последний, в свою очередь, имеет существенный недостаток – приблизительность в нахождении значений функции. Табличный метод избавляет от вычислений, но он тоже не нагляден.

Следует пояснить учащимся, что функцию можно задать и просто описанием: например, каждому числу х поставить в соответствие его целую часть, то есть у = [12].

d) Учащиеся «не видят» функцию, если она задана неявно, то есть если ее связь с аргументом задана с помощью уравнения (например, 3х – у + 1 = 0, ху = 5…).

 

е) Необходимо обратить внимание учащихся на различие области определения абстрактной функции и функции, полученной из конкретной задачи. (Например, у = х³,х R – абстрактная функция, у = а³, a 0 – функция из задачи про объем куба.) Для этого целесообразно предлагать учащимся задания на построение графиков на заданной области определения. Задания данного вида присутствуют только в учебнике А.Г. Мордковича. Например. Построить график функции у = f ( x ), где у = ,  …, где х , х … 

Полезно не ограничиваться одним типом упражнений «Найти область определения функции», а предложить выполнить творческие задания: «Построить функцию по заданной области определения».

Например. Построить функцию с областью определения Х:

1.х=(- ;1) (1; ) 2. х= (- ; 0) 3.х= . Ответ: 1. ; 2. ; 3.

3. Область определения и область изменения (значений) функции

Нередко учащиеся не видят разницы между областью определения функции и областью значений х, для которых имеет смысл аналитическое выражение, задающее функцию. Конечно, область определения функции не может быть шире области определения выражения, задающего функцию, но может быть уже.

Например, область определения выражения у = 2х² – 1, есть промежуток D (у) = ( ), но в упражнении может быть задана функция у = 2х² – 1 при х . Областью определения такой функции будет D(у) = , а если задан другой промежуток изменения х, то, строго говоря, и функция будет уже другой. Возможно, более логичным было бы, различая эти два понятия, говорить об области существования функции, имея в виду область определения аналитического выражения, задающего функцию.

Что касается области значений функции, то учащиеся хорошо понимают, что это такое, но при нахождении ее сталкиваются со значительными сложностями. Например: Найдите область значений функции

у = , у =

4. Обратная и сложная функции

Понятия обратной и сложной функций целесообразно ввести с определением функции, а не в 9 11 классах, когда учащиеся воспринимают его как нечто очень сложное. Разумеется, целесообразно не вводить строгие определения, а работать следующим образом:

- дать только начальные понятия;

- выработать умение изображать по данной функции функцию, обратную ей;

- сформировать первичный навык построения сложной функции.

а) Желательно составить с учащимися таблицу функций и функций, обратных им, изображая их графики (попутно делая выводы о симметричности графиков относительно прямой у = х.)

 

 

Исходная функция	Область определения исходной функции	Обратная функция	Область определения обратной функции	Графики
У = х2	0  х <	У =	0  х <	……….
…
…

в) Понятие «операция» на множестве функций в учебниках не вводится, хотя и используется: у = х + , у = . Полезно обсудить с учащимися, из каких функций и с помощью каких операций получилась рассматриваемая функция, прежде чем выполнить задание на нахождение области ее определения. В качестве пропедевтики понятия «композиция функции» можно рассмотреть пример у =  и показать, «как получилась функция от функции».

---

Дата добавления: 2019-09-02; просмотров: 1395; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!