Тема 3. МЕТОДИКА ИЗУЧЕНИЯ ЧИСЛОВЫХ СИСТЕМ
Одним из основных понятий математики является понятие числа. Изучение математики открывает знакомство с простейшим видом чисел — натуральными, и все последующее ее изучение связано с понятиями различных видов чисел.
Непосредственно связанным с понятием числа является понятие величины. Пожалуй, первые представления о величинах, а именно о частном виде величин — количестве предметов во множестве, было освоено людьми даже раньше, чем представление о числах. А дальнейшее историческое развитие понятия числа связано с развитием понятия величины и обусловлено им. По мере расширения понятия величины, введения новых видов величин, вводились, создавались, изобретались и новые классы чисел.
Математика изучает отдельные виды величин и чисел, дает им определения и устанавливает правила действий с числами и приёмы измерения величин. Но она не дает общего определения числа или величины вообще. Поэтому в школе изучается, главным образом, аппарат действий над разными видами чисел и измерения основных видов величин.
Понятия величины и числа создавались, изобретались всем человечеством на протяжении многих тысяч лет. При этом «число, величина – это понятия, то есть формы мысли, отражающие в обобщенном виде определенные свойства и отношения реальных предметов». Это значит, что в природе нет ни величин, ни чисел: они созданы, изобретены, человеком, его умом, и существуют лишь в его сознании. Но эти не реальные, а мысленные «создания» человека образуют его знания и умения, являются могучими орудиями, с помощью которых он создает все для себя и вокруг себя: материальную среду обитания, культуру, технику и производство.
|
|
|
3.1. Различные подходы к введению числовых множеств
«Понятие числа» - одна из самых важных и самых сложных тем школьного курса. Формирование понятия «число» происходит на протяжении всего курса обучения учащихся.
В 3 в. до н. э. Евклид определил число как «множество, составленное из единиц». Так же понимал число и Л.Ф. Магницкий. Но, в 18 веке применение этого определения встретилось с рядом трудностей. Согласно этому определению, 0; 1; дробь; иррациональные числа - не являются числами. Поэтому И.Ньютон вводит следующее определение числа: «число есть отношение одной величины к другой, того же рода, принятой за единицу». Изучение понятия «непрерывность» привело к уточнению понятия «иррациональное число». (Этим занимались Р. Дедекинд, Г. Кантор, К. Вейерштрасс), а развитие теории уравнения привело к понятию комплексного числа. В 19 веке в связи с развитием аксиоматического метода и разработкой основ математического анализа Г.Кантор дал определение натурального числа на основе понятия множество и равномощность, а Д. Пеано - основе сформулированных им аксиом[4]. Дальнейшее обобщение понятия числа и развитие учения о числе принадлежит Г. Кантору.
|
|
|
Исторически числовые множества расширялись следующим образом: N → N +{0}→ а/в-→ Z - → Q → R ., в современной математике порядок изучения чисел другой: : NcZcQcRcC .
Приверженность школы исторической последовательности объясняется тем, что понятие «дробь» доступнее учащимся, чем понятие «отрицательное число». (Историко – генетический метод введения понятия). Совершенствование методики преподавания позволило изучать отрицательные числа не в 7, а в 6 классе. Большую роль в этом сыграли работы Л.В. Занкова, П.Я. Гальперина, В.В. Давыдова. В рамках реформы образования 1967г. историческая схема развития числа была заменена на логическую (то есть была предпринята попытка сделать предметом изучения не число, а множества). Однако в ходе дальнейшей реформы был учтен действительный уровень развития логического мышления учащихся, поэтому пришлось отказаться от теоретико–множественного построения курса и чрезмерной строгости изложения материала. В отношении учения о числе это выразилось в некотором компромиссе – сочетании исторической и логической схем развития понятия «число».
|
|
|
В основе построения нового числового множества лежит принцип расширения, формулируемый следующим образом: «Пусть множество А расширяется до множества В, тогда необходимо выполнение следующих условий:
1. А  В.
В.
2. Все операции и отношения, выполняемые в А , должны выполнятся в В.
3. В В выполняется та операция, которая не выполняется в А.
4. Расширение идет по минимальности. (Нельзя N сразу расширить до Q).
В школьном курсе число будет считаться введенным, если:
– дано определение этого числа (часто описательного характера),
вытекающее из мотивирования необходимости его введения;
– для введенных чисел определяются отношения: =, >, <;
– дается определение алгебраических операций на множестве этих чисел;
– показывается, что в новом множестве выполнима «новая» операция.
Учебной целью изучения числовой линии является:
- формирование у учащихся знаний о числе и действий с ним;
-формирование вычислительных умений и их использование для решения практических задач;
- формирование вычислительной алгоритмической культуры.
|
|
|
В школьном курсе изучение отдельных числовых систем носит концентрический и многоэтапный характер. Понятие числа – это сложное понятие, усвоить которое можно лишь, изучив каждый вид чисел в отдельности и поняв процесс перехода от одного вида числа к следующему.
К понятию числа в математике существует два подхода: аксиоматический и конструктивный. В школьном курсе присутствуют элементы каждого из них.
Характеристика числовых множеств
| N | Z | Q | R |
| Бесконечное | Бесконечное | Бесконечное | Бесконечное |
| Упорядоченное | Упорядоченное | Упорядоченное | Упорядоченное |
| Дискретное | Дискретное | Дискретное | Всюду плотное и полное |
| С начальным элементом, но без конечного элемента | Без начального и конечного элементов | Без начального и конечного элементов | Без начального и конечного элементов |
| Замкнутое относительно операций «+», и «*», не замкнутое относительно операций «-» и «/» | Замкнутое относительно операций «+»,«*» и «-», не замкнутое относительно операции «/» | Замкнутое относительно операций «+», «*», «-», «/» (кроме 0) | Замкнутое относительно операций «+», «*», «-», «/» и операции сходимости любой сходимой последовательности (непрерывное) |
Схема расширения числового множества
| Исходное множество | Причины расширения исходного множества | Присоединяемое множество | Расширенное числовое множество |
| Натуральные числа | Вычитание равных чисел | Нуль | Целые неотрицательные числа |
| Целые неотрицательные числа | Вычитание из меньшего числа большего | Целые отрицательные числа | Целые числа |
| Целые числа | Деление нацело не всегда возможно | Дробные числа | Рациональные числа |
| Рациональные числа | Извлечение корня из любого положительного числа | Иррациональные числа | Действительные числа |
| Действительные числа | Извлечение корня из отрицательного числа | Мнимые числа | Комплексные числа |
Исходя из психологии ребенка, математических закономерностей и исторического развития математики при введении нового для учащихся числового множества учителю совместно с учащимися нужно выполнить ряд действий:
1. На специально подобранных задачах установить недостаточность известного на данном этапе числового множества для решения этой задачи и сделать вывод о необходимости расширения множества путем введения новых чисел.
2. Показать, что невозможность решения данных задач связана с невозможностью выполнения какого – либо действия в известном числовом множестве. Сделать вывод о необходимости расширения старого множества путем добавления таких новых чисел, чтобы в расширенном множестве выполнялись действия, которые раньше были невыполнимы или не всегда выполнимы.
3. Ввести новое число, дать ему название и определение.
4. Объединить известное множество и множество новых чисел. Дать ему название и проиллюстрировать место новых чисел на числовой прямой.
5. Показать, что предыдущее множество является подмножеством нового множества, решая соответствующие задачи.
6. Определить операцию сравнения и арифметические действия над числами как элементами нового множества. Вывести правила действий (коммуникативный, дистрибутивный законы и т. д.) над этими числами, установив, что для элементов нового множества они имеют тот же смысл, что и в прежнем множестве. Проиллюстрировать новые для учащихся факты на числовой прямой.
7. Организовать решение упражнений на действия с новыми числами. При этом:
-выделить в явном виде алгоритм и приемы вычислений;
- установить, что действие, ради которого производилось расширение, всегда выполнимо;
- подтвердить выполнимость в новом числовом множестве известных законов действий над числами. Заметим, что ни одно обратное действие, а из прямых – возведение в степень, не подчиняется переместительной закономерности.
8. Организовать решение текстовых задач с использованием новых чисел.
Этапы изучения числовых систем в курсе математики средней школы
| этап | класс | темы программы |
| Пропедевтичекий (нач. школа) | 1 - 4 | Счет, натуральный ряд, число 0.Запись и чтение чисел, четыре арифметических действия, сравнение чисел; доли и их запись с помощью дробей. Величины и их измерения, зависимость между ними, численное значение величин, числовые выражения. Правила и алгоритмы устных и письменных вычислений, приемы решения текстовых задач |
| Основная школа (курс арифметики 5 – 6 классов) | 5 | Натуральные числа. Сложение и вычитание натуральных чисел. Решение текстовых задач. Умножение и деление натуральных чисел. Решение задач арифметическим способом. Дробные числа. Сложение и вычитание десятичных дробей. Решение текстовых задач. Умножение и деление десятичных дробей. Проценты. Нахождение процентов. Начальные сведения о вычислениях на калькуляторе. Решение текстовых задач |
| 6 | Делимость натуральных чисел. Общие свойства обыкновенных дробей. Сложение и вычитание. Преобразование дробей. Умножение обыкновенных дробей. Деление обыкновенных дробей. Пропорции. Проценты. Решение задач на пропорции и проценты. Положительные и отрицательные числа. Понятие о рациональном числе. Действия с рациональными числами. Законы действий | |
| Завершающий (курс алгебры и начал анализа 7 – 11 классов) | 7 | Степень с натуральным показателем. Абсолютная и относительная погрешность приближенного значения |
| 8 - 10 | Квадратные корни. Понятие об иррациональном числе, общие сведения о действительных числах. Приближенное значение квадратного корня. Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Степень с целым показателем. Стандартный вид числа. Действия над приближенными значениями, их запись | |
| 11 | Показательная, логарифмическая, степенная функции. Корень n- степени, степень с рациональным показателем. Понятие о степени с иррациональным показателем. Логарифм числа |
К концу обучения в школе учащиеся должны четко представлять классификацию чисел:
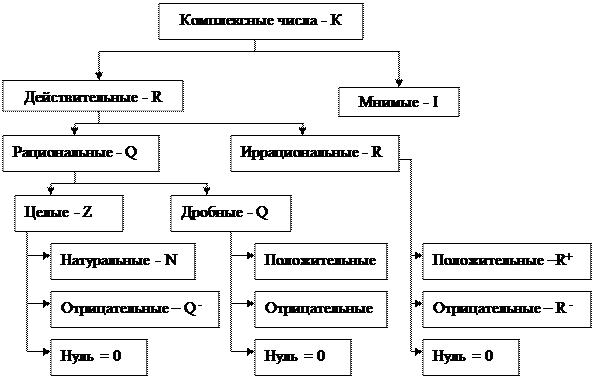

Множество натуральных чисел
Первое числовое множество, с которым сталкиваются учащиеся еще начальных классов - множество натуральных чисел. В математике существует два способа его построения. Количественные натуральные числа отождествляются с мощностью непустого конечного множества (построение по Кантору), порядковые натуральные числа построены на основе аксиом Пеано:
Натуральным числом называются элементы непустого конечного множества N , в котором существует отношение «непосредственно следует за» и выполняются аксиомы:
1. Существует натуральное число единица, не следующее ни за каким натуральным числом.
2. За каждым натуральным числом следует одно и только одно натуральное число.
3. Всякое натуральное число, кроме единицы, следует за одним и только одним натуральным числом.
4. Пусть М подмножество множества N. Если 1  , и из допущения, что натуральное число п
, и из допущения, что натуральное число п  М следует, что М принадлежит и п (число, непосредственно следующее за п), то M
М следует, что М принадлежит и п (число, непосредственно следующее за п), то M  N .
N .
В школьном курсе математики на наглядно-интуитивной основе представлены оба эти способа: каждое новое число появляется из анализа количества предметов, представленных на рисунках, а далее довольно четко выясняется и упорядоченность, и дискретность множества натуральных чисел.
Термин «натуральное число» ввел римский автор Боэций (475 – 524). Систематическое изучение натуральных чисел начинается в 5-м классе. Основная цель темы «Натуральные числа» - обобщение и закрепление тех сведений о множестве натуральных чисел, которые получены учащимися еще в начальной школе. Особое внимание уделяется позиционной записи любого натурального числа, выполнению поразрядного сравнения натуральных чисел. Вводятся символы = , >, <.
При изучении арифметических операций над натуральными числами учителю необходимо достаточно отчетливо представлять себе различие в требованиях к технике вычислений, к обоснованию этой техники и теории операций. К технике вычислений надо предъявлять самые жесткие требования - это основа (фундамент) всей вычислительной культуры учащихся. Твердого обоснования техники выполнения операций требовать не следует. Достаточно, если учащиеся будут выполнять эти операции и пользоваться их свойствами («на» - сложение или вычитание, «в» - умножение или деление). Наиболее дифференцированно приходится подходить к теории самих операций.
Понятие сложения вообще не определяется и считается интуитивно ясным из опыта предшествующего обучения. Хотя понятие вычитания тоже интуитивно ясно учащимся, но относительно него вводится строгое определение, которое остается неизменным для всех числовых и даже нечисловых множеств (вычесть из числа а число в - это значит найти такое число с, которое, будучи сложенным с числом в, даст число а). Операция умножения вводится специальным определением, справедливым лишь на множестве
N ( а * в = а+а+...+а). Деление опять строго определяется ( а:в = с <=> с*в = а).
в раз
Хотя глава и называется «Натуральные числа», фактически же в ней изучаются целые неотрицательные числа. И здесь ученики должны твердо усвоить двоякий смысл термина «нуль» (нуль - цифра и нуль - число). Поэтому необходимо научиться оперировать с нулем : 0+а = а; а+0 = а; 0*а = 0; а*0 = 0; 0:а = 0; обоснование невозможности деления на нуль в учебнике Н.Я. Виленкина проводится на основании определения операции деления: а:0 = х <=> х*0 = а, что неверно, 0:0 = х <=> х*0 = 0, но в качестве х можно взять любое число.
Лучшему усвоению учащимися множества натуральных чисел способствует изучение некоторых вопросов делимости. По отношению делимости на данное натуральное число n множество N разбивается на два непересекающихся класса: натуральные числа, делящиеся на n и натуральные числа, не делящиеся на n. По числу делителей - {простые}, {составные}, {1}. Рассматриваются признаки делимости на 2, 3, 5, 9, 10 и деление с остатком.
В результате изучения натуральных чисел у учащихся на наглядно-интуитивной основе должно быть сформировано:
1. знание свойств натуральных чисел (множество N - бесконечно, дискретно, упорядоченно, ограничено снизу);
2. понимание того факта, что операция умножения на N не определяется;
3. определение операции вычитание, умножение и деление;
4. умение работать с числами 0 и 1.
Теоретический материал в учебниках излагается в виде фрагментов, а затем идет решение задач и примеров.
В учебнике 5-го класса приводятся определения следующих понятий:
- натуральное число, десятичная запись числа, миллиард,
- координатный луч,
- сумма, разность, произведение двух натуральных чисел,
- числовое выражение,
- делитель числа, кратные числа,
- совершенное число, простое число, дружественные числа.
3.3.Методика изучения дробных чисел
Основным источником получения дробных чисел является практическая деятельность (дробь, как результат измерения, результат деления целого на равные части, как частное от деления целого числа на другое натуральное число). В учебнике Н.Я. Виленкина приводятся все три способа получения дробных чисел.
Первое знакомство учащихся с обыкновенными дробями происходит в 3 классе параллельно с изучением натуральных чисел. В 5 классе начинается систематическое изучение дробей. Десятичные дроби для учащихся не являются новыми числами по сравнению с обыкновенными дробями. Они представляют лишь другую запись ранее известных обыкновенных дробей со знаменателями 10, 100, 1000, так как в математических расчетах и при проведении практических работ наиболее удобны десятичные числа.
В методике математики существует проблема порядка изучения десятичных и обыкновенных дробей.
Возможные подходы к ее решению:
- сначала изучаются десятичные дроби, а потом – обыкновенные;
- сначала изучаются обыкновенные дроби;
- смешанный вариант изучения дробей.
В существующих учебниках придерживаются третьего варианта.
Порядок изучения дробей
| 5 класс | 6 класс |
| Обыкновенные дроби | Обыкновенные дроби |
| Сравнение, сложение и вычитание дробей с одинаковыми знаменателями | Сравнение дробей |
| Десятичные дроби | Арифметические действия с дробями |
| Четыре действия с десятичными дробями | Процент (по сути, изучение дес. дробей) |
Важным элементом методики изучения дробных чисел является убеждение учащихся в целесообразности их введения.
Возможность записи «доли» с помощью обыкновенных дробей является одним из приемов убеждения учащихся в полезности таких дробей.
Вторым приемом является тот факт, что с их помощью операция деления натуральных чисел делается всегда выполнимой.
Третий прием связан с измерением величин.
Тенденция на усиление роли теоретического обоснования имеет место и при изучении темы «Дроби».
3.3.1. Обыкновенные дроби
Методика введения обыкновенных дробей
В соответствии с программой по математике в начальной школе у учащихся должно быть сформировано понятие «доля». С помощью этого понятия у учащихся формируется понятие «обыкновенная дробь». Понятие «дробь» в учебнике Н.Я. Виленкина вводится на примере разрезания арбуза и деления отрезка на части, а в учебнике Дорофеева на примере разрезания торта. Оговаривается, что 1/2 это - половина,1/3 это - треть, 1/4 это - четверть.
В учебнике 3 класса записано: «Говорят, на первой тарелке лежит четвертая часть пирога, и пишут ¼ пирога; ¾ пирога. Такие числа, как 1/4, ¾ называются обыкновенными дробями. В дроби ¾ число 3 называют числителем дроби, а 4 – знаменателем дроби.»
Характеристика дроби всегда начинается со знаменателя. «Знаменатель показывает, на сколько равных частей разделен предмет, а числитель показывает, сколько таких частей надо взять».
Дается четкое определение дробных чисел. Обращается внимание на тот факт, что «две равные дроби – это различные обозначения одного и того же дробного числа, например, ½ = 2/4».
В 5 классе происходит лишь знакомство учащихся с обыкновенными дробями, их изучение продолжается в 6 классе.
Основное содержание учебников «Математика - 5»
| Н.Я. Виленкин Определение Записи вида 5/8 называют обыкновенными дробями. В дроби 5/8 число 5 называют числителем дроби, число 8 знаменателем дроби. | Г.В. Дорофеев Определение Специальную “двухэтажную запись” 2/3 называют дробью, где 2 - числитель, а 3 – знаменатель. |
| Знаменатель показывает, на сколько долей делят, числитель сколько таких долей взято. Числитель дроби пишут над чертой знаменатель под чертой. | Вводится определение правильных и неправильных дробей, но учащихся не знакомят с алгоритмом перевода смешанного числа в неправильную дробь и алгоритмом выделения целой части. |
| Дроби можно изображать на координатном луче. | Дроби можно изображать на координатном луче. |
В учебниках много заданий типа:
Какая часть фигуры закрашена?
 
|
Закрасьте 5/6 фигуры, 3/5
 
|
| Сколько сантиметров в 2/5метра? Сколько минут в 1/5 часа? Какаю часть составляют 10гр от килограмма? Какие числа на координатной прямой соответствуют точкам …? Отметьте точки … … … на координатном луче | |
| Из 30 дней 2/5 были дождливыми, сколько было солнечных дней …? Восстановите запись */4=2/8. Приведите дроби 2/7 , 3/28, 1/14 к знаменателю 56. Выразите в метрах 30 см, 10мм, 140см … Какая из точек лежит левее на координатном луче? Сравните дроби … и т.д. |
| Приводятся образцы правильного чтения дробей и алгоритма правильного решения задачи (например, 876 на стр197) | Чем больше частей, тем меньше доля. | |||||||||||
Равные дроби
2/4 = 1/2 | Равные дроби
2/4 = 1/2 | |||||||||||
| На координатном луче равные дроби соответствуют одной точке. Две равные дроби обозначают одно и тоже дробное число. | ||||||||||||
Нет основного свойства дроби.
Дробные числа с одинаковыми знаменателями можно сравнивать, складывать, вычитать и делить.
- Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель и больше та у которой числитель больше.
- Точка на координатном луче, имеющая меньшую координату лежит слева от точки имеющей большую координату.
(Есть упражнение на правильное чтение неравенств.)
Правильные и неправильные дроби.
Объясняется, что если числитель равен знаменателю, число равно 1(8/8=1)
Пример с пирогом ( 2 пирога разрезаны на 8 частей каждый. Взяли целый пирог и еще 3 части получили 11/8)
С учащимися отрабатывается тот факт, что правильная дробь 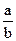 <1, а неправильная <1, а неправильная 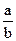  1. 1.
| Основное свойство дроби: - Если числитель и знаменатель умножить на одно и тоже число отличное от нуля, то получится дробь равная данной. (Есть запись правила с помощью букв.) - На координатном луче равные дроби соответствуют одной точке. Приводя дробь к новому знаменателю, говорят о дополнительном множителе. Вводится правило сокращения дроби. Вводится определение несократимой дроби. Сравнение дробей. - Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель и больше та у которой числитель больше. - Если дроби с разными знаменателями их приводят к общему (наименьшему) знаменателю и потом сравнивают. |
| Вводится определение Сложения и вычитания дробей с одинаковыми знаменателями. (Учащимся объясняется, что если знаменатели разные, доли тоже разные, поэтому складывать и вычитать их мы не можем.) Не вводится правило сложения и вычитания дробей с разными знаменателями. Учащихся знакомят с буквенной записью правил a/b+c/b=a+c/d. Деление и дроби. (Знак деления можно заменить дробной чертой.) Смешанные числа. Сложение смешанных чисел. | Натуральные числа и дроби. Дробное число. (Знак деления можно заменить дробной чертой.) Сложение вычитание дробей с одинаковыми знаменателями. - Если дроби с разными знаменателями их приводят к общему (наименьшему) знаменателю и потом складывают. Смешанные числа. Сложение смешанных чисел |
Методическая схема введения понятия «обыкновенная дробь»
-Выполнить материализованные действия по делению предмета на 4 равные части.
- Сообщить термины: «одна четвертая», «три четвертых»…
- Ввести запись: ¾, ¼…
- Ввести термины «обыкновенная дробь», «числитель, знаменатель дроби».
- Дать содержательную характеристику дроби (что показывает знаменатель дроби, числитель дроби).
- Привести примеры дробей.
Особую трудность технического характера представляют собой операции сложения и вычитания обыкновенных дробей с разными знаменателями, так как при сложении или вычитании дробей ребенок должен выполнить следующие логических операции:
-проанализировать знаменатели;
-если они неравные, то найти наименьший общий знаменатель;
-найти дополнительные множители;
-привести дроби к общему знаменателю;
-сложить или вычесть числители;
-сократить, если возможно; выделить целую часть.
В учебнике Н.Я. Виленкина эти трудности распределяются на два года. В 5 классе рассматривается сожжение и вычитание дробей только с одинаковыми знаменателями, а в 6 классе - с разными знаменателями.
Наиболее сложным в методическом плане является введение понятия «умножение дробей» в 6 классе. Наиболее удачное его рассмотрение дано в учебнике Н.Я. Виленкина. На данном этапе обучения учитель имеет возможность обосновать законы умножения и их справедливость на множестве дробей.
Пример Почему переместительный закон умножения справедлив на множестве дробей? а/в * с/к = ас/вк = са/кв = с/к а/в.В основе доказательства лежит правило умножения натуральных чисел.
3.3.2. Методика изучения десятичных дробей
Введение понятия десятичной дроби
| Учебники Раздел учебника | Виленкин Н..Я. Математика 5 | Нурк Э.Р. Тельман А.Э. Математика 5 | Дорофеев Г.В. Математика 6 | Математика5-6 Учебник- собеседник | СовайленкоВ.К. Система обучения мат-ке в 5-6кл | Десятичные дроби Myми Доле |
| Раздел, в котором вводится понятие «Десятич. дроби» | Глава II Дробные числа. П. 6 Десятичные дроби. Сложение и вычитание десят. дробей. Десятичная запись дробных чисел. | Глава IV Дробные числа. Сложение и вычитание десят. Дробей п.4.6. Десятичные дроби. | Глава III Десятичные дроби П. 13. Как записыв-ся и читаются десятичные дроби. | Глава II Дробные числа П. 7. Десятичные дроби и действия над ними Урок 63. Что такое десятичная дробь? | Глава XI Понятие десятичной дроби. Преобразование десятичных дробей П. 109 Какие дроби наз-ся десят.-ми? Как читаются и записываются десятичные дроби? | Глава 6. В которой появляются десятичные дроби. |
| Понятия, на которые делается опора при введении нового понятия | Глава 1. Натуральные числа. Глава2 Дробные числа. П.5 Обыкновен. дроби. | Глава IV Др. числа. Сложение и вычитание дес. дробей. П.4.1 Обык. дроби. | Обык. дроби (введены в 5 классе). | Глава II Дробные числа П.6 Дроби и действия над ними. | Глава VIII Основные понятия о дроби Глава IХ Задачи на дроби. Глава Х Преобр. обык.д. Сложен и вычитание дробей с одинак. знаменат. | Нуль и натуральные числа. |
| Содержание пункта, в котором вводиться новое понятие | Новые понятия: Десят. дробь. (Пояснение как читаются и записываются дес. дроби). | Новые понятия: Десят.д. Новые термины: целая часть, дробная часть, десятичные знаки. (Пояснение как читаются, как записываются дроби. Дается четкое правило записи дес. дроби). | Новые понятия: Десят.д. (Дается четкое правило чтения и записи дес. дроби. Содержаться исторические сведения. Показывается изображение десятичных дробей на координатной прямой). | Новые понятия: Десят. дробь. (Поясняется как читается дес. дробь. Дается четкая запись дес. дроби. Показан способ набора дес. д. на микрокалькуляторе). | Новые понятия: Десят. д. Термины: десятич. знаки. (Поясняется как читается и записывается дес. дроби. | Новые понятия: Десятич. Дробь (Поясняется как читается и записывается дес. дробь). |
Схема введения понятия «десятичная дробь»
1. Мотивация к изучению темы
Задача. Ширина доски равна 6 дм 3 см необходимо выразить ее в сантиметрах.
Решение. 6 дм 3 см = 63 см. Чтобы выразить ту же ширину в дециметрах, придется использовать дроби. Так как 1см=  дм, то 3см=
дм, то 3см= 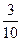 и потом 6дм=
и потом 6дм=  дм. Таким же образом находим 4ц 17кг=
дм. Таким же образом находим 4ц 17кг= 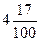
2. Формулировка определения. Знаменатель дробной части числа  равен 10, а у числа
равен 10, а у числа  он равен 100.
он равен 100.
Числа со знаменателями 10, 100, 1000 и т. Д. условились записывать без знаменателя.
Правило записи. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой (Для неправильной дроби).
- Если дробь правильная, то перед запятой записывается 0.
Определение. Такую запись дробей называют десятичной, а сами дроби – десятичными.
3. Понятие о разрядах в десятичных дробях
В записи натурального числа значение цифры зависит от того, в каком разряде он находиться. Единицы двух соседних разрядов отличны друг от друга в 10 раз.
Для записи десятичных дробей используются новые разряды, которые пишутся справа от разряда единиц, поставив после него запятую.
В этих разрядах указывают доли единиц. В первом разряде после запятой указывают число десятичных долей, его так и называют разряд десятые. Во втором указывают число сотых долей, его так и называют разряд сотых.
| Десятки тысячных | Тысячи | Сотни | Десятки | Единицы | Десятые | Сотые | Тысячные | Десятитысячные | Стотысячные | Миллионные | |
| 3 | 8 | 1 | 4 | 2 | , | 4 | 0 | 2 | 1 | 5 | 7 |
Чтение десятичных дробей.При чтении десятичной дроби сначала называется ее часть, стоящая до запятой, а затем часть, стоящая после запятой, с добавлением названия последнего разряда.
7,35 – семь целых и тридцать пять сотых
7,35 содержит 7 единиц, 3 десятых, 5 сотых.
При записи десятичной дроби последнюю цифру помещают в том разряде, который произносят при ее чтение.
Ноль целых, восемь тысячных – 0, 018.
В десятичной дроби после запятой должно быть столько же цифр, сколько нулей в записи знаменателя обыкновенной дроби.
5,13 =  5,00013=
5,00013= 
2цифры=2нуля 5цифр = 5 нулей
4. Изображение чисел на координатном луче
Десятичные дроби, как и обыкновенные, можно изображать на координатном луче. Отметим на нём 0,3. Для этого берем отрезок от 0 до 1, делим его на 10 (так как последняя цифра стоит в разряде десятых) и отсчитываем 3 части (начиная от нуля).
|
|
|
 . . . . . . . . . . .
. . . . . . . . . . .
Построим 0,36. Сначала делим отрезок на 10 частей, а затем еще на десять десятую долю отрезка, следующего за 0,3.
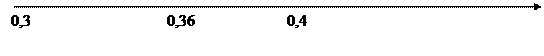 . . . . . . . . . . .
. . . . . . . . . . .
5. Сложение и вычитание десятичных дробей
Правило. Чтобы сложить (вычесть) десятичные дроби, надо:
– уравнять в этих дробях количество знаков после запятой (дописав нули после имеющихся цифр в числе);
– записать их друг под другом так, чтобы запятая была расположена под запятой;
– выполнить сложение (вычитание), не обращая внимания на запятую;
– поставить в ответе запятую под запятой в данных дробях.
Пример: Вычислить значение выражения 23,756+4,8.
1) 23,756+4,8=23,756+4,800= 28,556; (дописать нули в разряды после запятой в сотые и тысячные у второго числа)
23,756
+
4,800
28,556
6. Умножение десятичных дробей
Правило . Чтобы умножить десятичную дробь на натуральное число, надо:
– умножить ее на это число, не обращая внимания на запятую;
– в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Пример: 7,84*92 =721,28.
7,84
 92
92
1568
+
7056
721,28
Правило 2. Чтобы умножить десятичную дробь на 10, 100,1000 и так далее, надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
1,0073* 100 = 100,73 (запятая перенесена вправо на 2 цифры)
Правило 3. Чтобы перемножить две десятичные дроби, надо:
– выполнить умножение, не обращая внимания на запятые;
– отделить в полученном произведении запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Пример: 9,45* 0,012 = 0,1134

Правило 4. Чтобы умножить десятичную дробь на 0,1, надо:
– запятую в дроби перенести влево на 0,01;
– запятую перенести влево на две единицы.
Пример: 0,056* 0,1= 0,0056.
7. Деление десятичных дробей
Правило 1. Чтобы разделить десятичную дробь на натуральное число, надо:
– разделить ее на это число, не обращая внимания на запятую;
– поставить в частном запятую, когда закончится деление целой части.
Правило 2. Чтобы разделить десятичную дробь на 10, 100, 1000 и так далее, надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Пример: 8,92:100 = 0,0892.
Правило 3. С помощью деления находят десятичную дробь, равную данной обыкновенной дроби. Для этого надо поделить числитель на знаменатель дроби.
Пример: 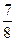 = 7:8 =0,875.
= 7:8 =0,875.
Правило 4. Чтобы разделить число на десятичную дробь, надо:
– в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
– после этого выполнить деление на натуральное число
Пример 160,23 : 4,9 = 1602,3:49=32,7.
Правило 5: Чтобы разделить десятичную дробь на 01; 0,01 и так далее, надо перенести в ней запятую вправо на столько цифр, сколько нулей стоит в делителе перед единицей.
Пример: 7,23:0,1=72,3
8. Типы упражнений:
- Назовите число единиц каждого разряда…
- Какая цифра записана в данном разряде…?
- Прочитайте следующие десятичные дроби…
- Запишите в виде десятичной дроби…
- Запишите десятичные дроби в виде обыкновенных и сократите их…
- Какие числа отмечены точками на координатном луче…?
- Начертите на координатном луче следующие числа…
- Какую часть метра составляют…?
- Выразить в тоннах, метрах…
- Измерьте ширину тетради и выразите ее в дециметрах…
- Расположите числа в порядке возрастания…
- Какие натуральные числа заключены между дробями…?
-Вычислите сумму, разность дробей…
- Увеличьте, уменьшите каждое число в … раз.
-Какое число нужно прибавить к данному чтобы получить следующее число…?
- Решите задачи …
9. Согласно программе Министерства РФ, учащиеся должны приобрести следующие знания и умения:
Дата добавления: 2019-09-02; просмотров: 7062; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



