Лекция 3. Электрические цепи однофазного синусоидального тока 2 страница
j sin a . (3.16)
|
A& (t ) можно записать
A& (t ) = A m
e j (w t+y a ) = A
cos(w t +y a )+
jA m
sin(w t +y a
). (3.17)
Действительная часть выражения (3.17) представляет собой функцию, изменяющуюся по закону косинуса, а мнимая часть — функцию, изменяющуюся по закону синуса:
Re A& (t ) = A m cos(w t +y a ), Im A& (t ) = A m si n(w t +y a ), (3.18)
где Re A& (t ) и Im A& (t ) обозначают операции взятия действительной и мнимой части
комплексного числа
A& (t ). Из (3.18) следует, что любую синусоидальную функцию
a(t ),
определяемую формулой (3.13), можно записать так:
a(t ) = A m si n(w t +y a ) = Im{A e a }= Im A& (t ). (3.19)
 |
j (w t+y )
Соотношение (3.19) называется комплексной или символической формой записи
синусоидальной величины
a(t ), а функция
A& (t ) = A m
e j (w t +y a )
(3.20)
— ее комплексным мгновенным значением. Графическое представление комплексной
функции A& (t ) аналогично представлению синусоидальных величин вращающимися
векторами (рисунок 3.6, б). Это означает, что синусоидальную величину a(t ) можно
изобразить на комплексной плоскости как проекцию вращающегося вектора A& (t ) на
ось + j (рисунок 3.6, б). При неизменной частоте тока в цепи (w = const ) указанное
|
|
|
изображение принято рассматривать для момента времени
t = 0
в виде комплексной
амплитуды
A&m или комплексного действующего значения (комплекса) A& :
A&m
= A m
e j y a ,
A& = Ae j y a , (3.21)
где
A = A m
— действующее значение
a(t ).
Различные формы комплексного представления синусоидального тока, напряжения и ЭДС показаны в таблице 3.2.
Таблица 3.2 – Комплексное представление синусоидального тока, напряжения и ЭДС
| Синусоидальная величина | Сила тока | Напряжение | ЭДС |
| Функциональное представление | i(t ) = I m sin(w t +y i ) | u(t ) = U m sin(w t +y u ) | e(t ) = E m sin(w t +y e ) |
| Символическое (комплексное) представление | i(t ) = Im{I e j (w t+y i )} m | u(t ) = Im {U e j (w t+y u )} m | e(t ) = Im {E e j (w t +y e )} m |
| Комплексное мгновенное значение | I& (t ) = I e j (w t+y i ) m m | U& (t ) = U e j (w t+y u ) m m | E& (t ) = E e j (w t+y e ) m m |
| Комплексная амплитуда | I& = I e j y i m m | U& = U e j y u m m | E& = E e j y e m m |
| Комплекс величины | I& = Ie j y i | U& = U e j y u | E& = Ee j y e |
Пр и мечание – Комплексная амплитуда A&m и комплекс A& содержат информацию
только о двух параметрах синусоиды — амплитуде
|
|
|
A m и начальной фазе y a , не отражая
ее третьего параметра — угловую частоту . Поэтому переход от комплексной формы
представления величин к форме мгновенных значений осуществляется согласно формулам
|
e j w t },
a(t ) = Im{
2 A& e j w t }. (3.22)
3.4 Комплексное сопротивление и комплексная проводимость
Изображение синусоидальных токов и напряжений в виде комплексных амплитуд
I&m ,
U& m
или комплексов I& , U& приводит к необходимости сопоставления указанных
величин по амплитуде и фазе для одного и того же элемента цепи или ее части, рассматриваемой в целом как пассивный двухполюсник. Это сопоставление проводят также с помощью комплексных чисел.
Отношение комплексного напряжения на зажимах двухполюсника к комплексному току в нем называется комплексным сопротивлением:
U& U e j y u
U j (y -y ) j
Z = I& =
Ie j y i = I e
u i = Ze j
, (3.23)
где Z — модуль, а — аргумент комплексного сопротивления. Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению действующего напряжения к действующему значению тока, а аргумент комплексного сопротивления
|
|
|
— разности начальных фаз напряжения и тока:
Z = U ,
I
j =y u
-y i
. (3.24)
Величина, обратная комплексному сопротивлению, т.е. функция
1 I&
Ie j y i
I - j (y -y ) - j
Y = =
Z U&
= Ue j y u = U e
u i = Ye j
, (3.25)
равная отношению комплексного тока в двухполюснике к комплексному напряжению на нем, называется комплексной проводимостью.
В выражении (3.25) Y — модуль, а (- j ) — аргумент комплексной
проводимости. Модуль комплексной проводимости, называемый полной проводимостью, равен отношению действующего значения тока к действующему напряжению, а аргумент комплексной проводимости — разности начальных фаз тока и напряжения:
Y = I ,
U
- j =y i
-y u
. (3.26)
Примечание – Комплексное сопротивление и комплексную проводимость можно также определить через комплексную амплитуду тока и напряжения:
Z = U& m ,
I&m
Y = I&m
U& m
. (3.27)
3.5 Пассивные элементы в цепи синусоидального тока. Понятие об активном, индуктивном и ёмкостном сопротивлении двухполюсника
|
|
|
Для учета процессов преобразования электрической энергии в схемы замещения цепей синусоидального тока вводят пассивные двухполюсные элементы: резистивный, индуктивный и ёмкостный. Основные сведения об этих элементах приведены в таблице 3.3.
Таблица 3.3 – Пассивные двухполюсные элементы
| Пассивный двухполюсный элемент и его условное обозначение | Резистивный | Индуктивный | Ёмкостный |
|
| 
| |
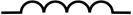
| Основной параметр | R – сопротивление | L – индуктивность | C – ёмкость |
| Сопротивление переменному току | R – активное | X L = w L – индуктивное | X C = 1 (w C ) – ёмкостное |
| Проводимость при переменном токе | g = 1 R – активная | b L = 1 X L – индуктивная | b C = 1 X C – ёмкостная |
| Комплексное сопротивление | Z R = R | Z L = jX L | Z C = - jX C |
Продолжение таблицы 3.3
| Пассивный двухполюсный элемент и его условное обозначение | Резистивный | Индуктивный | Ёмкостный | |
|
| 
| ||
| Комплексная проводимость | Y R = g | Y L = - jb L | Y C = jb C | |
| для мгновенных значений | i = u R | u = L di dt | i = C du dt | |
|
Соотношение между током | для амплитудных значений | I = U m , m R I m = gU m | I = U m , m X L I m = b L U m | I = U m , m X C I m = b C U m |
| и напряжением (закон Ома) | для действующих значений | I = U , R I = gU | I = U , X L I = b L U | I = U , X C I = b C U |
| для комплексных | I& = U& , Z R | I& = U& , Z L | I& = U& , Z C | |
| значений | I& = Y R U& | I& = Y L U& | I& = Y C U& | |
| Ток и напряжение в элементе | i = I m sin(w t +y i ), u = U m sin(w t +y u ) | |||
| Соотношение между начальной фазой тока и напряжения | y i =y u | y =y - p i u 2 | y =y + p i u 2 | |
3.5.1 
Резистивный элемент в цепи переменного тока. Понятие об активном сопротивлении резистора
Ток и напряжение в резистивном элементе с сопротивлением R (рисунок 3.7, а) связаны законом Ома вида
i = u . (3.28)
R
 |  |  |
а) б) в)
Рисунок 3.7 – Резистивный элемент (а), временная (б) и векторная (в) диаграммы тока и напряжения в сопротивлении
равна:
При синусоидальном напряжении
u = U m sin(w t +y u )
сила тока согласно (3.28)
i = u
R
= U m sin(w t +y
R u
) = I m
sin(w t +y i
). (3.29)
Из (3.29) следует, что амплитуды тока и напряжения связаны соотношением
а их начальные фазы — соотношением
I = U m , (3.30)
m R
y i =y u , (3.31)
т.е. в цепи с резистивным элементом угол сдвига фаз j =y u -y i = 0 , следовательно,
ток и напряжение в идеальном резисторе изменяются синфазно. Временная диаграмма токов и напряжений в резисторе показана на рисунке 3.7, б; соответствующая векторная диаграмма — на рисунке 3.7, в.
Сопротивление R резистивного элемента при переменном токе несколько больше его сопротивления при постоянном токе, определяемого по формуле
R = r l ,
S
где — удельное сопротивление проводника, l — его длина, S — площадь поперечного сечения. Это обусловлено так называемым поверхностным эффектом, при котором плотность переменного тока у поверхности проводника всегда больше, чем во внутренних участках его сечения, что эквивалентно уменьшению площади его поперечного сечения. Поэтому сопротивление резистивного элемента при переменном токе называют активным сопротивлением, а при постоянном токе — электрическим сопротивлением. Величина, обратная активному сопротивлению, т.е.
называется активной проводимостью.
g = 1 , (3.32)
R
Выражение (3.30) определяет закон Ома для резистивного элемента
относительно амплитудных значений. Разделив это выражение на
Ома относительно действующих значений тока и напряжения:
, получим закон
I = U ,
Дата добавления: 2019-07-15; просмотров: 171; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!