Закон Ома и напряжение на неоднородном участке цепи с источником

Закон Ома может быть сформулирован для участка цепи, содержащего источник

ЭДС, т.е. для неоднородного участка (рисунок 2.7).

а) б)

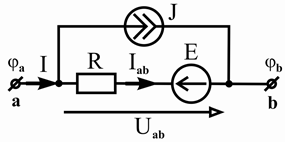
Рисунок 2.7 – Схема неоднородного участка электрической цепи

Как следует из рисунка 2.7, для неоднородного участка цепи возможны два случая:

1) ток на участке цепи течет в направлении действия ЭДС (рисунок 2.7, а);

2) ток на участке цепи течет против направления действия ЭДС (рисунок 2.7, б).

Рассмотрим 1-й случай (рисунок 2.7, а) и определим напряжение граничными точками « a » и « b » участка цепи.

U ab

между

На однородном участке « ac » ток I течет от точки « a » к точке « c », т.е. в

направлении от более высокого потенциала j a к более низкому потенциалу j c , поэтому

j a > j c и на основании (2.11) получаем уравнение

U ac = j a - j c = IR ,

из которого выражаем потенциал j a :

j a = j c + IR . (2.13)

На участке « cb » действует только ЭДС E в направлении от точки « c » к точке

« b », т.е. в направлении от более низкого значения потенциала j c к более высокому

значению j b , поэтому j c < j b и

j b - j c = E ,

откуда следует равенство

j b = j c + E . (2.14)

На основании формул (2.13) и (2.14) получим

U ab = j a - j b = (j c + IR)- (j c + E ) = -E + IR

или

U ab = -E + IR . (2.15)

Повторяя аналогичные рассуждения для схемы рисунка 2.7, б, докажем, что

U ab = E + IR . (2.16)

Из уравнений (2.15) и (2.16) получим обобщенную формулу для определения

напряжения на неоднородном участке электрической цепи с источником ЭДС:

U ab = ±E + IR . (2.17)

Из (2.17) также следует выражение закона Ома для неоднородного участка цепи:

I = ± E + j a - j b

= ± E + U ab . (2.18)

В таком виде закон Ома позволяет определить ток на участке « ab », если известна величина ЭДС источника и направление ее действия:

Примечание – В формуле (2.18) ЭДС E берется со знаком «+», если ее

направление на участке цепи совпадает с направлением тока (рисунок 2.7, а); со знаком «–», если противоположно току (рисунок 2.7, б).

В формуле (2.17), наоборот, при совпадении направлений тока и ЭДС величина E

берется со знаком «–», при несовпадении — со знаком «+».

2.3.3 Закон Ома и напряжение на неоднородном участке цепи с источниками ЭДС и тока

Соотношения (2.17) и (2.18), определяющие величину напряжения и закон Ома для неоднородного участка цепи, были получены на основании схемы замещения, содержащей источник ЭДС. Рассмотрим теперь общий случай, когда на участке цепи присутствуют оба типа источников электрической энергии: источник ЭДС E и источник тока J .

Схемы замещения неоднородного участка цепи с двумя разнотипными источниками энергии E и J , называемые также схемами замещения обобщенной ветви, представлены на рисунке 2.8.

а) б)

в) г)

Рисунок 2.8 – Схемы замещения обобщенной ветви

Из этого рисунка следует, что в зависимости от направления ЭДС E , задающего

тока J и тока обобщенной ветви I возможны четыре типа схем замещения. Рассмотрим 1-ю из них, изображенную на рисунке 2.8, а, и получим формулу для

определения напряжения U ab

при известном значении тока I .

На неоднородном участке « ab » напряжение U ab

основании формулы (2.15):

можно выразить через ток

I ab на

Сам ток

I ab

U ab = -E + I ab R . (2.19)

согласно 1-му закону Кирхгофа может быть выражен через задающий

ток источника J и ток обобщенной ветви I :

I ab = -J + I . (2.20)

Из (2.19) и (2.20) тогда получается равенство

U ab = -E - JR + IR . (2.21)

Повторяя аналогичные рассуждения для схем, изображенных на рисунках 2.8, б – 2.8, г, получим следующие уравнения:

U ab = -E + JR + IR ,

U ab = E - JR + IR ,

U ab = E + JR + IR . (2.22)

Из формул (2.21) и (2.22) следует обобщенная формула для определения напряжения на неоднородном участке цепи, содержащем источники ЭДС и тока:

U ab = ±E ± JR + IR . (2.23)

Из (2.23) следует также выражение закона Ома для обобщенной ветви:

I = ± E ± JR + j a - j b

= ± E ± JR + U ab . (2.24)

Примечание – В формуле (2.24) ЭДС E или задающий ток J берутся со знаком «+», если их направления на участке цепи совпадают с направлением тока I ; со знаком «–», если противоположны току I .

В формуле (2.23), наоборот, при совпадении направления тока I с направлениями ЭДС E или задающего тока J величины E и J берутся со знаком «–», при несовпадении указанных направлений — со знаком «+».

2.3.4 Закон Ома для замкнутой одноконтурной цепи

Закон Ома может быть сформулирован для замкнутой одноконтурной

цепи (рисунок 2.9).

Рисунок 2.9 – Схема одноконтурной электрической цепи

В этом случае

j a = j b

(падение напряжения в соединительных проводах не

учитывается) и из формулы (2.17) следует

I = E

, (2.25)

где

R ист

R + R ист

— внутреннее сопротивление источника.

2.4 Потенциальная диаграмма

Потенциальной диаграммой называется график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления в той последовательности, в которой они включены в контур цепи, а по оси ординат — потенциалы соответствующих точек.

Рисунок 2.10 – Схема разветвленной электрической цепи

Полагая потенциал точки « a » равным нулю (j a = 0 ), определим потенциалы остальных точек контура « abcdefa » (рисунок 2.10), совершая обход в направлении движения часовой стрелки:

j b = j a + I1R1 , j c = j b + E1 , j d = j c + I1R4 ,

j e = j d - E4 , j f = j e - I2R2 , j a = j f - E2 = 0 .

Пример потенциальной диаграммы для контура « abcdefa » приведен на рисунке 2.11.

Рисунок 2.11 – Потенциальная диаграмма

Наклон прямых на участках диаграммы определяется величиной тока и поэтому

одинаков для сопротивлений

R1 и

R4 , по которым протекает один и тот же ток

I1 .

2.5 Работа и мощность постоянного тока. Уравнение баланса мощностей

Работа A , совершаемая электрическим полем при перемещении положительного заряда q вдоль неразветвленного однородного участка электрической цепи, равна

произведению величины этого заряда на напряжение U между граничными точками участка:

A = qU . (2.26)

При равномерном движении заряда в течение времени t , т.е. при постоянном токе

I = const , величина заряда q = It и работа согласно (2.26)

A = IUt . (2.27)

Для резистивных элементов соотношение (2.27) можно преобразовать, воспользовавшись законами Ома в виде

I = U

тогда вместо (2.27) получатся равенства

или

U = IR ,

U 2

A = I

Rt ,

A = t . (2.28)

Интенсивность совершения работы электрическим током характеризуется его

мощностью P . По определению

P = A , (2.29)

т.е. мощность равна отношению величины работы A к промежутку времени t , в течение которого эта работа производилась. Из (2.27) – (2.29) следует, что мощность постоянного тока может быть рассчитана по одной из следующих формул:

P = IU ,

P = I

2R ,

P = . (2.30)

Единица измерения работы: [ A ] = 1Дж (джоуль); единица измерения мощности: [ P ] = 1Вт (ватт). Практической единицей измерения работы служит киловатт- час (кВт · ч), т.е. работа, совершаемая при неизменной мощности 1 кВт в течение 1 ч.

Так как 1 Вт · с = 1 Дж, то 1 кВт · ч = 3600 000 Дж.

)

В цепях с произвольной структурой выполняется условие баланса мощностей, согласно которому алгебраическая сумма мощностей всех источников энергии равна арифметической сумме мощностей всех приемников энергии:

k =1

(P ист

k =å

)

k =1

пр k

, (2.31)

где m и n — количества источников и приемников энергии, действующих в цепи,

P ист

и P пр

— их соответствующие мощности.

Соотношение (2.31) является следствием закона сохранения энергии и называется

уравнением баланса мощностей.

Примечания

1 Мощность источника ЭДС E в уравнении (2.31) положительна, т.е. P ист = EI > 0 , если направление ЭДС E совпадает с направлением тока I (рисунок 2.12, а). В противном случае мощность источника ЭДС считается

отрицательной:

P ист = -EI < 0 (рисунок 2.12, б).

2 Мощность источника тока J в уравнении (2.31) положительна, т.е.

P ист = UJ > 0 , если направление тока J внутри источника и направление напряжения

U между его выводами противоположны (рисунок 2.12, в). В противном случае

мощность источника тока считается отрицательной: P ист = -UJ < 0 (рисунок 2.12, г).

3 Мощность приемника с сопротивлением R в резистивной цепи постоянного

тока всегда положительна и определяется по формуле

P пр

= I 2R .

а) б) в) г)

Рисунок 2.12 – Схема, иллюстрирующая правила выбора знаков мощностей источников ЭДС (а), (б) и источников тока (в), (г) при составлении уравнения баланса

Для схемы цепи, изображенной на рисунке 2.10, уравнение баланса мощностей, к примеру, выглядит так:

(- E + E )I - E I + (- E + E )I = I 2 (R + R )+ I 2R + I 2R .

1 4 1 2 2

3 5 3 1 1 4

2 2 3 3

2.6 Основные методы анализа простых электрических цепей

Простыми электрическими цепями называют цепи с одним источником энергии. При этом в качестве приемников могут быть несколько резистивных элементов, соединенных последовательно или параллельно.

2.6.1 Анализ простых электрических цепей при последовательном и параллельном соединении резистивных элементов

Схемы последовательного и параллельного соединения резистивных элементов показаны на рисунке 2.13, основные свойства этих соединений, являющиеся следствиями законов Кирхгофа, систематизированы в таблице 2.1.

а) б)

Рисунок 2.13 – Последовательное (а) и параллельное (б) соединение резистивных элементов

Таблица 2.1 – Соотношения для токов, напряжений и сопротивлений при последовательном и параллельном соединениях резистивных элементов

Тип соединения	Последовательное	Параллельное
Сила тока	I = const	I = I1 + I2 +K+ I n , I k = Ug k , k = 1,n
Напряжение	U = U1 + U 2 +K+ U n , U k = IR k , k = 1,n	U = const
Сопротивление (проводимость)	R = R1 + R2 +KR n	g = g1 + g2 +K+ g n

Примечание – Величина

g = 1 R

(см. таблицу 2.1) называется проводимостью;

единица измерения проводимости: [ g ] = 1См (сименс).

2.6.2 Анализ простых электрических цепей при смешанном соединении резистивных элементов. Метод эквивалентных преобразований и метод пропорциональных величин

Если в простой электрической цепи часть элементов соединена последовательно, а часть параллельно, то имеет место смешанный способ соединения. Токи в ветвях схемы при смешанном соединении элементов можно найти, используя метод эквивалентных преобразований (метод свертывания) или метод пропорциональных величин (метод подобия).

Сущность метода эквивалентных преобразований заключается в том, чтобы группы из последовательно и параллельно соединенных резистивных элементов заменить эквивалентным сопротивлением, зная которое, определить для полученного простого контура ток в неразветвленной части цепи и, выполнив обратное преобразование, рассчитать токи в остальных ветвях схемы.

а) б)

Рисунок 2.14 – Схемы иллюстрирующие применение метода эквивалентных преобразований (а) и метода пропорциональных величин (б)

Определим, например, методом эквивалентных преобразований токи схеме цепи, изображенной на рисунке 2.14, а.

I1 ,

I2 и I3 в

Эквивалентное сопротивление R этой цепи относительно зажимов источника можно найти по формуле

R = R + R

= R +

R2R3 ,

1 23

R2 + R3

где величина

R23

обозначает сопротивление участка цепи с параллельным соединением

элементов R2

и R3

(рисунок 2.14, а). Ток

I1 в неразветвленной части цепи рассчитаем

на основании закона Ома

I = E ,

а затем, определив по формуле U 23 = I1R23

величину напряжения U 23

на параллельном

участке с элементами R2 и R3 , найдем два остальных тока также по закону Ома:

I = U 23 ,

I = U 23 .

Сущность метода пропорциональных величин состоит в том, чтобы в самой удаленной от источника ЭДС ветви произвольно задать некоторое (ненулевое) значение силы тока, например 1А, зная которое, определить токи в остальных ветвях, а также

соответствующее им значение ЭДС

E * . Затем, сравнив полученное значение E * с

заданным по условию значением E , найти коэффициент пропорциональности

k = E E *

и рассчитать действительные токи

I1 ,

I2 , … , I n

в ветвях схемы, умножив

полученные значения токов

I * ,

I * , … ,

* на коэффициент k :

I = kI * , I = kI * , … , I = kI * . (2.32)

1 1 2 2 n n

Определим, например, методом пропорциональных величин токи уже рассмотренной схеме цепи на рисунке 2.14, а.

I1 ,

I2 и I3 в

Положим

I * = 1

и найдем соответствующую этому значению величину ЭДС

E * ,

т.е. такую, которая бы обеспечивала протекание в ветви с сопротивлением величиной в 1А (рисунок 2.14, б).

R3 тока

Напряжение

* на параллельно соединенных сопротивлениях

R2 и

R3 следует

определить как падение напряжения

* на сопротивлении

R3 , т.е. по формуле

U * = U * = I * R , а ток I * в сопротивлении R — на основании закона Ома

23 3 3 3 2 2

I * = U * R . Тогда ток I *

в неразветвленной части цепи можно рассчитать согласно

2 23 2 1

формуле

I * = I * + I * , а значение искомой ЭДС E *

согласно равенству

1 2 3

E * = U * + U * = I * R + U * ,

1 23 1 1 23

где величина

U * = I * R означает падение напряжения на сопротивлении R при токе

1 1 1 1

I * . Далее, определив коэффициент пропорциональности

k = E

E * , можно вычислить

действительные токи

I1 ,

I2 и I3

по формулам (2.32).

2.7 Основные методы анализа сложных электрических цепей

Сложной электрической цепью называют цепь, содержащую две (и более) ветви с источниками электрической энергии. При анализе таких цепей в ветвях соответствующих им схем замещения предварительно указывают условно положительные направления токов. Далее составляют, следуя 1-му и 2-му законам Кирхгофа, структурные уравнения. Добавление к ним компонентных соотношений

приводит к законченной формулировке задач анализа. Дальнейшие действия приобретают чисто вычислительный характер.

Существуют приемы, позволяющие облегчить постановку задачи на математическом уровне. В разделах 2.7.1 – 2.7.6 описаны методы, реализующие подобные приемы. Это — метод непосредственного применения законов Кирхгофа, метод контурных токов, метод наложения (суперпозиции), метод узловых потенциалов метод, метод двух узлов и метод эквивалентного генератора.

2.7.1 Метод непосредственного применения законов Кирхгофа

Самым общим методом расчета электрических цепей является метод непосредственного применения законов Кирхгофа (метод уравнений Кирхгофа). Суть его заключается в составлении системы уравнений в соответствии с 1-м и 2-м законами Кирхгофа и решении этой системы относительно неизвестных токов. Система уравнений разрешима, если все входящие в нее уравнения являются линейно независимыми и число уравнений в системе равно числу неизвестных величин (числу токов).

Порядок расчета электрической цепи методом уравнений Кирхгофа

1) Обозначить на схеме цепи токи в ветвях и произвольно выбрать их положительные направления.

2) Для узлов электрической цепи составить уравнения по 1-му закону Кирхгофа.

Общее количество таких уравнений

n1 = m -1, где m — число узлов в цепи.

3) Выбрать независимые замкнутые контуры электрической цепи и для каждого из них составить уравнение по 2-му закону Кирхгофа Общее количество таких

уравнений

n2 =

p - m - k + 1, где p — число ветвей цепи, k — число источников тока.

4) Решить составленную систему уравнений относительно неизвестных токов.

5) Проверить правильность решения задачи путем составления уравнения баланса мощностей.

Рисунок 2.15 – Схема, иллюстрирующая применение метода уравнений Кирхгофа

Схема, изображенная на рисунке 2.15, содержит 2 узла и 3 ветви, т.е. m = 2 ,

p = 3 и k = 0 (отсутствуют источники тока). Количество уравнений на основании 1-го

закона составит

n1 = 1, количество уравнений на основании 2-го закона —

n2 = 2 . По 1-

му закону Кирхгофа для узла « a » получаем уравнение

- I1 + I2 - I3 = 0 ,

по 2-му закону Кирхгофа для контуров « abcda » и « adefa » уравнения

I1(R1 + R4 )+ I2R2 = E1 + E2 - E4 , - I2R2 - I3(R3 + R5 ) = -E2 + E3 - E5 .

Эти уравнения в совокупности образуют систему линейных алгебраических

уравнений, решением которой являются токи

Примечания

I1 ,

I2 ,

I3 .

1 Контуры цепи, выбранные для составления уравнений по 2-му закону Кирхгофа (см. пункт 3 алгоритма), следует считать независимыми, если в каждом из них есть хотя бы одна ветвь, не принадлежащая остальным контурам.

2 Если при решении системы уравнений Кирхгофа, значения некоторых токов получаются отрицательными, это означает, что их действительные направления противоположны произвольно выбранным.

3 Общее число независимых уравнений n , которые получаются на основании 1-го и 2-го законов Кирхгофа равно:

n = n1 + n2 = (m -1)+ ( p - m - k + 1) = p - k .

Если источники тока в цепи отсутствуют ( k = 0 ), то общее число уравнений

n = p , т.е. совпадает с количеством ветвей в цепи (с количеством неизвестных токов).

2.7.2 Метод контурных токов

В методе контурных токов в качестве промежуточных переменных выбирают токи, замыкающиеся в каждом контуре и называемые контурными. В этом случае уравнения составляют только по 2-му закону Кирхгофа относительно контурных токов. Очевидно, что общее количество таких уравнений всегда совпадает с числом

независимых контуров в цепи, т.е. с числом n = p - m - k + 1.

Порядок расчета электрической цепи методом контурных токов

1) Обозначить на схеме цепи действительные токи в ветвях и произвольно выбрать их положительные направления.

2) Выбрать n = p - m - k + 1 независимых контуров электрической цепи и

произвольно задаться направлением контурных токов в них.

3) Для каждого выбранного контура относительно протекающих в его ветвях контурных токов составить уравнение по 2-му закону Кирхгофа. При этом положительное направление обхода контура полагать совпадающим с направлением соответствующего контурного тока.

4) Решить полученную систему уравнений относительно неизвестных контурных

токов.

5) Действительный ток в каждой ветви определить как алгебраическую сумму

контурных токов, замыкающихся через эту ветвь. При этом те из контурных токов, направления которых совпадут с направлением действительного тока, войдут в указанную алгебраическую сумму со знаком «+», в противном случае — со знаком «–».

Схема цепи, изображенная на рисунке 2.16, имеет n = 2 независимых контура, в

которых циркулируют два контурных тока:

I11

— контурный ток 1-го контура и

I22 —

контурный ток 2-го контура. Эти токи являются решением системы уравнений

⎧ (R1 + R2 + R4 )I11 - R2I22 = E1 + E2;

⎨- R I + (R + R + R )I = -E - E .

(2.33)

⎩ 2 11

2 3 5 22 2 3

Действительные токи

I1 ,

I2 , I3

ветвей (см. рисунок 2.16) определятся линейными

комбинациями контурных токов:

I1 = I11 ,

I2 = I11 - I22 ,

I3 = -I22 .

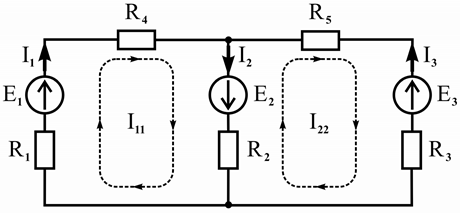
Рисунок 2.16 – Схема, иллюстрирующая применение метода контурных токов

Обобщая систему уравнений (2.33) на случай электрической цепи с произвольным количеством независимых контуров n , можно получить следующую систему для

определения контурных токов

I11 ,

I22 , … ,

I nn :

⎧ R11I11 + R12I22 +K+ R1n I nn = E11;

⎪

⎪R21I11 + R22I22 +K+ R2n I nn = E22;

(2.34)

⎪

⎨ ...............................................

Здесь

R kk

⎪⎩R n1I11 + R n 2I22 +K+ R nn I nn = E nn.

( k = 1,n ) — собственное (полное) сопротивление k - го контура,

R km

( k ,m = 1,n

и k ¹ m ) — сопротивление связи контуров с номерами k и m

(сопротивление смежной ветви),

E kk

( k = 1,n ) — контурная ЭДС k - го контура.

Так, например, в системе уравнений (2.33) контурные сопротивления

R11 и

R22

равны:

R11 = R1 + R2 + R4 ,

R22 = R2 + R3 + R5 ; сопротивления связи:

R12 = -R2 ,

R21 = -R2 ; контурные ЭДС:

E11 = E1 + E2 ,

E22 = -E2 - E3 .

Система контурных уравнений (2.34) может быть представлена в матричной форме:

RI = E , (2.35)

где R — квадратная матрица сопротивлений цепи порядка n , I — матрица-столбец искомых контурных токов, E — матрица-столбец контурных ЭДС, причем

⎡R11

⎢

R12 R22

K R1n ⎤

⎥

K 2n

⎡ I11 ⎤

⎢ ⎥

⎡ E11 ⎤

⎢ ⎥

R = ⎢

⎢ M

⎥ ,

M M M ⎥

I = ⎢ ⎥ ,

⎣

nn ⎦

⎢ M ⎥

E = ⎢ ⎥ .

⎣

nn ⎦

⎢ M ⎥

⎣

nn ⎦

⎢R R

K R ⎥

⎢I ⎥

⎢E ⎥

Решение матричного уравнения (2.35) определяет равенство

I = R -1 E , (2.36)

где

R -1 — матрица обратная к R .

Решение системы уравнений (2.34) можно также записать и через определители,

т.е. на основании метода Крамера:

I11 = Ä

E11 E22 M

E nn

R12 R22 M

R n 2

K R1n

K R2n , K ,

M M

K R nn

I nn = Ä

R11 R21 M

R n1

R12 R22 M

R n2

K E11

K E22 . (2.37)

M M

K E nn

Символом здесь обозначен главный определитель системы алгебраических уравнений (2.34) (определитель матрицы R ):

Ä = det R =

R11 R21 M

R n1

R12 R22 M

R n 2

K R1n

K R2n

M M

K R nn

. (2.38)

Формулам (2.37), (2.38) можно придать более компактную форму, если разложить числитель каждой из дробей (2.37) по элементам столбца, в котором собраны значения контурных ЭДС:

I kk

= E11

Ä1k Ä

+ E22

Ä2k

+K+ E nn

Ä nk

, (2.39)

где

Ä mk

( m = 1,n ) — алгебраическое дополнение элемента

R mk

определителя (2.38):

Ä mk

= (-1)m+k Ä *

. (2.40)

Здесь

* обозначает минор элемента

R mk , т.е. определитель, полученный из

вычеркиванием его m - й строки и k - го столбца.

Примечания

1 Собственное сопротивление R kk > 0 контура с номером k равно сумме всех

сопротивлений, образующих этот контур.

2 Сопротивление связи

R km

( R km = R mk ) равно алгебраической сумме

сопротивлений, включенных в ветвь, являющуюся общей для контуров с номерами k и

m . Эту величину в системе уравнений (2.34) записывают со знаком «+», если

направления контурных токов

I kk

и I mm , замыкающихся через рассматриваемую ветвь,

совпадают. В противном случае сопротивлению

R km

приписывают знак «–». Если

контуры k и m не имеют общих ветвей, сопротивление связи

R km = 0 .

3 Контурная ЭДС

E kk

контура с номером k равна алгебраической сумме всех

ЭДС, присутствующих в этом контуре, причем со знаком «+» берутся те из них, направления которых совпадают с направлением обхода контура k (с направлением

контурного тока

I kk ). В противном случае входящие в

E kk

ЭДС берутся со знаком «–».

4 В системе уравнений (2.34), а также в эквивалентном ей матричном уравнении (2.35) предполагается, что источники энергии заданы в виде источников ЭДС. Если же по условию задачи часть источников будет задана в виде источников тока, то перед началом расчета их целесообразно преобразовать в эквивалентные источники ЭДС согласно формулам (2.10).

2.7.3 Принцип и метод наложения

Метод наложения позволяет определить токи в ветвях электрической цепи непосредственно по закону Ома. Этот метод основан на принципе наложения (или

суперпозиции), суть которого состоит в том, что ток в любой ветви линейной электрической цепи, содержащей несколько источников ЭДС, можно рассматривать как алгебраическую сумму частичных токов, созданных в этой ветви действием каждой ЭДС в отдельности.

Порядок расчета электрической цепи методом наложения

2) Исходную схему с несколькими источниками ЭДС представить совокупностью расчетных схем, в каждой из которых действует только одна ЭДС. При этом все остальные источники ЭДС из текущей расчетной схемы следует исключить, оставив лишь их внутренние сопротивления.

3) В ветвях каждой расчетной схемы определить токи, возникающие от действия только одной ЭДС — частичные токи.

4) Действительные токи ветвей исходной схемы рассчитать как алгебраические суммы (наложения) соответствующих частичных токов расчетных схем. При этом те частичные токи, направления которых совпадут с направлениями действительных токов, войдут в указанные алгебраические суммы со знаком «+», в противном случае — со знаком «–».

На рисунке 2.17 представлена схема электрической цепи с двумя источниками ЭДС, расчет которой методом наложения может быть выполнен на основании расчетных схем, изображенных на рисунке 2.18.

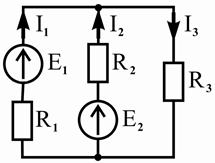
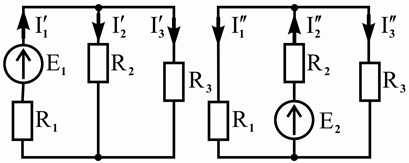
Рисунок 2.17 – Исходная

схема

Рисунок 2.18 – Расчетные схемы с частичными

токами

Принимая направления действительных токов

I1 ,

I2 , I3

в исходной схеме

рисунка 2.17 за положительные, выполним алгебраическое суммирование (наложение)

частичных токов расчетных схем, изображенных на рисунке 2.18:

I1 = I1¢ - I1¢ , I2 = -I2¢ + I2¢ , I3 = I3¢ + I3¢ .

Здесь

I1¢,

I2¢ ,

I3¢ означают частичные токи первой расчетной схемы,

I1¢ ,

I2¢ ,

I3¢ —

частичные токи второй расчетной схемы.

Примечание – Принцип наложения применим для расчета линейных электрических цепей не только по токам, но и по напряжениям, так как они линейно связаны с токами. Для расчета мощности этот принцип применять нельзя, так как мощность является не линейной, а квадратичной функцией тока или напряжения:

P = I 2R

или

P = U 2 R .

2.7.4 Метод узловых потенциалов

Если для произвольной электрической цепи известны потенциалы всех ее узлов,

то ток I в любой ветви этой цепи можно определить по закону Ома:

I = (± E + j a - j b )g , (2.41)

где E — величина ЭДС, j a и j b — потенциалы узлов « a » и « b » схемы, g — полная

проводимость ветви, подсоединенной к этим узлам.

Метод расчета электрических цепей, в котором за неизвестные принимаются потенциалы узлов схемы, называется методом узловых потенциалов. Для упрощения расчетов один из узлов схемы предварительно заземляют, полагая его потенциал

равным нулю. Если, например, электрическая цепь содержит n + 1 узлов и потенциал

j n+1 = 0 , то потенциалы остальных узлов j1, j2 , … , j n схемы относительно опорного

(или базового) узла с потенциалом j n+1 определяются из системы уравнений:

⎧ G11j1 + G12j2 +K+ G1n j n = J11;

⎪

⎪G21j1 + G22j2 +K+ G2n j n = J 22;

(2.42)

⎪

⎨ ...............................................

⎪⎩G n1j1 + G n2j2 +K+ G nn j n = J nn ;

где

G kk

( k = 1,n ) — собственная проводимость узла k ,

G km

( k ,m = 1,n ,

k ¹ m ) —

проводимость связи узлов k и m ,

J kk

— узловой ток k - го узла.

Закон Ома (2.41) и система уравнений (2.42) составляют математическую основу метода узловых потенциалов.

Система уравнений узловых потенциалов (2.42) может быть представлена в матричной форме:

G j = J , (2.43)

где G — квадратная матрица проводимостей цепи порядка n , — матрица-столбец искомых потенциалов узлов, J — матрица-столбец узловых токов, причем

⎡G11

⎢

G12 G22

K G1n ⎤

⎥

K 2n

⎡j1 ⎤

⎢ ⎥

⎡ J11 ⎤

⎢ ⎥

G = ⎢

⎥ , j = ⎢ ⎥ ,

J = ⎢ ⎥ .

⎢ M M M M ⎥

⎢ M ⎥

⎢ ⎥ ⎢ ⎥ ⎢ ⎥

⎣G n1

G n 2

K G nn ⎦

⎣j n ⎦

⎣J nn ⎦

Решение матричного уравнения (2.43) определяет равенство

j = G -1 J , (2.44)

где G -1 — матрица обратная к G .

Примечания

1 Собственная проводимость

всех ветвей, сходящихся в этом узле.

G kk

( G kk

> 0 ) узла k равна сумме проводимостей

3 Проводимость связи

G km £ 0

( G km = G mk ) узлов k и m равна взятой со знаком

«–» сумме проводимостей всех ветвей, соединяющих эти узлы. Если между узлами k и

m нет соединяющей их ветви, проводимость связи G km = 0 .

4 Узловой ток

J kk

узла k определяется равенством

p q

J kk

=åE i g i +åJ i , (2.45)

i=1 i=1

где

E i и g i

— величина ЭДС и проводимость ветви, присоединенной к узлу k ,

J i —

ток источника тока, также присоединенного к этому узлу. ЭДС

E i и ток

J i в

формуле (2.45) берутся со знаком «+», если они направлены к рассматриваемому узлу, со знаком «–», если они направлены от узла.

Рисунок 2.19 – Схема, иллюстрирующая применение метода узловых потенциалов

Схема, изображенная на рисунке 2.19, содержит 3 узла, обозначенные цифрами 1,

2 и 3. Если положить потенциал j3 = 0 , то потенциалы 2-х остальных узлов j1 и j2

являются решением следующей системы уравнений:

⎨

⎧G11j1 + G12j2 = J11;

⎩G21j1 + G22j2 = J 22.

При этом

G11 = g1 + g2 + g3 ,

G12 = G21 = -g3 ,

G22 = g3 + g4 + g5 ,

J11 = E1g1 - E3g3 - J6 + J7 ,

J22 = E3g3 - E4 g4 + E5 g5 - J7 , где

g i = 1 R i

( i = 1,5 ) —

проводимости ветвей схемы с сопротивлениями R1 ,

можно рассчитать согласно формуле (2.41):

R2 , R3 , R4 и R5 , токи в которых

I1 = (j3 - j1 + E1 )g1 , I2 = (j3 - j1 )g2 , I3 = (j1 - j2 + E3 )g3 ,

I4 = (j2 - j3 + E4 )g4 , I5 = (j2 - j3 - E5 )g5 .

2.7.5 Метод двух узлов

В разветвленной электрической цепи с двумя узлами все ветви соединены параллельно и находятся под действием одного и того же (узлового) напряжения (рисунок 2.20). Метод расчета электрических цепей, в котором за промежуточную переменную принимают напряжение между двумя узлами схемы, называется методом узлового напряжения или методом двух узлов.

Расчетный алгоритм метода двух узлов может быть построен на основании метода узловых потенциалов как его частный случай. Действительно, полагая в схеме

рисунка 2.20 j2 = 0 , легко получить формулу для расчета узлового напряжения

U0 = j1 - j2 из системы уравнений (2.42). Эта система уравнений в применении к схеме

рисунка 2.20 вырождается в одно уравнение вида G11j1 = J11, из которого согласно (2.45) следует формула

m p

åE k g k +åJ k

U0 = k = 1 k = 1 , (2.46)

åg k k =1

где ЭДС E k

и ток источника J k

берутся со знаком «+», если их направления

противоположны направлению узлового напряжения направления совпадают.

U0 , со знаком «–», если их

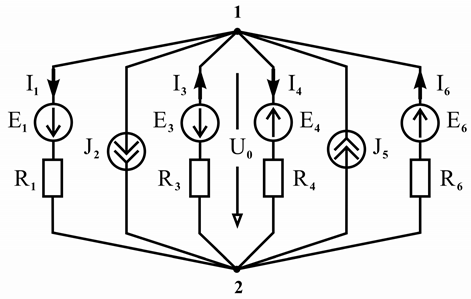
Рисунок 2.20 – Схема, иллюстрирующая применение метода двух узлов

Ток в каждой ветви схемы с двумя узлами определяется по формуле аналогичной (2.41), которая в данном случае имеет вид:

I k = (± E k ± U0 )g k , (2.47)

где ЭДС E k

и узловое напряжение U0

записывают со знаком «+», если их направления

совпадают с током

I k , со знаком «–», если противоположны току.

Для схемы, изображенной на рисунке 2.20, например, узловое напряжение равно:

U = - E1g1 - E3g3 + E4 g4 + E6 g6 - J 2 + J5 ,

g1 + g3 + g4 + g6

а токи I1 , I3 , I4 и I6

рассчитываются согласно формулам

I1 = (E1 + U0 )g1,

I3 = (- E3 -U0 )g3 , I4 = (- E4 + U0 )g4 ,

I6 = (E6 -U0 )g6 .

2.7.6 Метод эквивалентного генератора

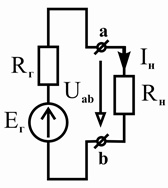
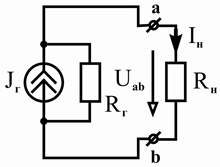
Метод эквивалентного генератора (метод активного двухполюсника, метод холостого хода и короткого замыкания) применяется, когда по условию задачи необходимо определить ток (или напряжение) в отдельной ветви цепи. Для этого фрагмент схемы, ток через который требуется вычислить, рассматривают как пассивный двухполюсник (выделяют из цепи), а всю остальную часть схемы, внешнюю по отношению к выделенному участку, представляют активным двухполюсником (рисунок 2.21, а).

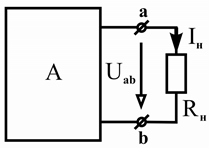
а) б) в)

Рисунок 2.21 – Замена активного двухполюсника (а) эквивалентным источником напряжения (б) или эквивалентным источником тока (в)

Дальнейшие действия сводятся к корректной замене активного двухполюсника

эквивалентным источником энергии (эквивалентным генератором), т.е. таким, который

обеспечивал бы на полюсах исследуемого фрагмента такой же ток напряжение U ab , что и в исходной схеме (рисунок 2.21, а).

I н и такое же

Очевидно, что сделать это можно двумя способами — активный двухполюсник

можно заменить эквивалентным источником напряжения с ЭДС E г

и внутренним

сопротивлением

R г (рисунок 2.21, б) или эквивалентным источником тока с задающим

током J г

и внутренней проводимостью G г

= 1 R г

(рисунок 2.21, в).

При известных значениях параметров

E г , R г

или

J г , G г

ток в выделенной ветви,

например, ветви « ab » (рисунок 2.21), определяется на основании закона Ома:

E г

I н = R + R ,

I н =

J г

1+ G R

, (2.48)

г н г н

где

R н — сопротивление выделенной ветви.

Правила, по которым активный двухполюсник заменяется эквивалентными

источниками, устанавливает теорема Тевенена для источника напряжения и теорема Нортона для источника тока.

Теорема Тевенена: ток в некоторой ветви, присоединенной к активному двухполюснику, не изменится, если этот двухполюсник заменить источником напряжения с ЭДС, равной напряжению на зажимах двухполюсника в режиме холостого хода, и сопротивлением, равным входному сопротивлению двухполюсника:

E г = U хх , R г = R вх , (2.49)

где U хх

и R вх

— указанные в теореме Тевенена напряжение холостого хода и входное

сопротивление двухполюсника.

Теорема Нортона: ток в некоторой ветви, присоединенной к активному двухполюснику, не изменится, если этот двухполюсник заменить источником тока с величиной задающего тока, равной току короткого замыкания двухполюсника, и проводимостью, равной входной проводимости двухполюсника:

J г = I кз , G г = G вх , (2.50)

где

I кз

и G вх = 1 R вх

— указанные в теореме Нортона ток короткого замыкания и

входная проводимость двухполюсника.

Способ определения обобщенных параметров

U хх

и I кз

активного

двухполюсника в символической форме представлен на рисунке 2.22.

а) б)

Рисунок 2.22 – Определение напряжения на зажимах источника ЭДС (а)

и задающего тока источника тока (б)

Формулы (2.48) с учетом (2.49) и (2.50) преобразуем к виду:

I н =

U хх ,

R + R

I н =

I кз

1 + G R

. (2.51)

вх н вх н

Соотношения (2.51) являются расчетными формулами метода эквивалентного генератора.

Примечания

1 Внутреннее сопротивление

R вх

активного двухполюсника равно сопротивлению

такого пассивного двухполюсника, который может быть образован из исходного исключением всех источников энергии, находящихся внутри него. При этом подразумевается, что источники ЭДС в ветвях активного двухполюсника в процессе исключения следует закоротить, а ветви, содержащие источники тока, разомкнуть. Пример такого преобразования демонстрируют схемы на рисунке 2.23.

а) б)

Рисунок 2.23 – Активный двухполюсник (а) и соответствующая схема замещения для определения его входного сопротивления (б)

2 Параметры U хх ,

I кз ,

R вх

определяются расчетным путем или экспериментально.

В последнем случае величины

U хх ,

I кз

находят непосредственно по показаниям

приборов (вольтметра и амперметра), проводя опыты холостого хода и короткого

замыкания согласно схемам рисунка 2.22, а входное сопротивление

R вх

определяют

косвенно по результатам обоих опытов. Так, при формул (2.51) получаем

R н = 0

(опыт короткого замыкания) из

R = U хх . (2.52)

вх I

кз

2.7.7 Передача энергии от активного двухполюсника к нагрузке. КПД источника энергии

Любую сколь угодно сложную электрическую цепь с несколькими источниками энергии всегда можно представить в виде активного двухполюсника, соединенного с пассивным двухполюсником (рисунок 2.24, а). Активный двухполюсник обычно характеризуют совокупностью источников электрической энергии, а пассивный — совокупностью пассивных приемников.

а) б)

Рисунок 2.24 – Замена разветвленной цепи активным и пассивным двухполюсником (а) и схема замещения для исследования условий передачи энергии в цепи активного двухполюсника (б)

В соответствии с теоремами об эквивалентных источниках (теоремами Тевенена и Нортона) многоэлементный активный двухполюсник можно заменить двухэлементным

активным двухполюсником (эквивалентным генератором) с параметрами

E г , R г в

случае источника ЭДС или

J г , G г

в случае источника тока. Пассивный двухполюсник

можно представить одним резистивным элементом (нагрузкой) с единственным

параметром R н

(сопротивлением нагрузки).

Исследуем условия передачи электрической энергии от активного двухполюсника к нагрузке на примере схемы замещения цепи с эквивалентным источником ЭДС

E г (рисунок 2.24, б). Данную схему, в частности, можно интерпретировать как схему

замещения линии электропередач с идеальными (без сопротивления) проводами.

Переменный резистор R н

сопротивлением.

в этом случае символизирует нагрузку с изменяющимся

В зависимости от величины сопротивления нагрузки R н

выделяют следующие

режимы работы электрической цепи, представленной активным двухполюсником:

1) режим холостого хода ( R н = ¥ ), при котором нагрузка отключена от

источника энергии, ток в цепи отсутствует, напряжение источника наибольшее, равное величине ЭДС: U хх = E г ;

U хх

на разомкнутых зажимах

2) режим короткого замыкания ( R н = 0 ), при котором зажимы источника

замкнуты накоротко, напряжение на них равно нулю, в цепи протекает ток короткого

замыкания

I кз = E г

R г ;

3) согласованный режим ( R н = R г ), при котором сопротивление нагрузки равно внутреннему сопротивлению источника;

4) номинальный режим, при котором источник и нагрузка работают при

номинальных значениях токов и напряжений

I ном ,

U ном , т.е. при тех значениях, на

которые они рассчитаны заводами-изготовителями.

При исследовании условий передачи энергии в цепи различают следующие типы мощностей:

1) полная мощность

P г — вся мощность, вырабатываемая источником энергии;

2) мощность потерь P — мощность, расходуемая внутри источника, либо в соединительных проводах;

3) полезная мощность P н

— мощность, потребляемая нагрузкой.

Для схемы замещения, изображенной на рисунке 2.24, б указанные типы мощностей определяются равенствами

P г = E г I ,

Ä P = I 2R ,

P = I 2R

. (2.53)

Так как сила тока в цепи при этом

I =

то из (2.53) следует:

E г ,

R г + R н

P г = г ,

E 2R

Ä =

P г г ,

E R

P н = г н . (2.54)

R г + R н

(R г + R н )

Кроме того, полную и полезную мощности можно еще представить равенствами

P = I 2 (R + R ), P = UI , P = (E - IR )I , (2.55)

н н н г г

где U = IR н = E - IR г

— напряжение на нагрузке (на сопротивлении

R н ).

Эффективность передачи энергии в электрических цепях оценивается

коэффициентом полезного действия (КПД). Величина КПД определяется

отношением полезной мощности

P н к величине полной мощности источника

P г :

h = P н

P г

= P н

P н + Ä P

. (2.56)

На основании (2.53), (2.54) и (2.56) можно также получить следующие формулы для определения КПД:

h = R н ,

R г + R н

h = 1- ÄP ,

P г

h = 1- IR г . (2.57)

E г

Определим величину сопротивления нагрузки

R н , при которой полезная

мощность P н

достигает максимального значения. Для этого найдем первую

производную полезной мощности P н по R н

основании (2.54) получаем уравнение

и приравняем ее к нулю. На

dP (R + R )2 - 2R (R + R )

н= E 2 г н н г н= 0 ,

dR н

(R г

+ R н )

решением которого является равенство

R н = R г . (2.58)

Соотношение (2.58) называется условием передачи максимальной энергии приемнику. Из этого условия следует, что наибольшая полезная мощность будет потребляться нагрузкой в согласованном режиме работы цепи, когда сопротивление нагрузки равно внутреннему сопротивлению источника энергии.

Из (2.54) и (2.58) следует, что в режиме согласованной нагрузки мощности

P г ,

P и P н

равны:

E 2

P г г ,

2R г

E 2

Ä =

P г ,

4R г

E 2

P н г , (2.59)

4R г

поэтому КПД цепи согласно (2.57) и (2.59)

h = 0.5 , т.е. половина энергии источника

ЭДС E г

преобразуется в теплоту за счет его внутреннего сопротивления

R г . При

передаче больших мощностей работа в согласованном режиме, как правило,

недопустима. В цепях большой мощности непременным условием является т.е. обеспечение возможно большего КПД.

R н >> R г ,

Основные закономерности режимов работы источника энергии представлены в

таблице 2.2.

Таблица 2.2 – Режимы работы источника энергии

Режимы работы источника энергии	R н	U	I	P г	P	P н
Холостой ход	¥	E	0	0	0	0	1
Короткое замыкание	0	0	E г R г	E 2 г R г	E 2 г R г	0	0
Согласованный	R г	E г 2	E г 2R г	E 2 г 2R г	E 2 г 4R г	E 2 г 4R г	0.5
Номинальный	R ном	U ном	I ном	P г ном	Ä P ном	P н ном	h ном

На рисунке 2.25 построены зависимости

P г (I ),

Ä P(I ),

P н (I )

и h(I ). Эти

зависимости называют энергетическими характеристиками цепи.

Рисунок 2.25 – Энергетические характеристики цепи постоянного тока

Примечание – Соблюдение номинального режима обеспечивает эффективное и экономичное производство и потребление электрической энергии. Чаще всего

номинальный режим работы активного и пассивного двухполюсников соответствует случаю, когда сопротивление эквивалентного приемника много больше внутреннего сопротивления эквивалентного генератора ( R н >> R г ). При этом КПД электрической цепи близок к единице (h » 1), что очень важно для силовых (мощных)

электротехнических устройств. Для некоторых маломощных устройств, используемых, например, в радиотехнике, электронике и автоматике, важным является достижение максимально возможной мощности приемника. В этих случаях стремятся обеспечить согласованный режим работы источников и приемников электрической энергии, который является для них номинальным режимом.

2.8 Эквивалентные преобразования электрических схем. Основные методы

Анализ разветвленных электрических цепей во многих случаях можно упростить путем эквивалентных преобразований. Эквивалентным преобразованием части схемы электрической цепи называется такое преобразование, при котором токи и напряжения вне преобразованной части остаются неизменными. Целесообразное преобразование электрической схемы приводит к уменьшению числа ее ветвей или узлов, а, следовательно, и числа уравнений, необходимых для ее расчета.

2.8.1 Преобразование соединения резистивных элементов звездой в эквивалентное соединение треугольником и обратное преобразование

Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рисунок 2.26, а), называется соединением «звезда» ( Υ ), а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рисунок 2.26, б) — соединением «треугольник» ( Δ ).

а) б)

Рисунок 2.26 – Схема соединения резистивных элементов звездой (а) и треугольником (б)

Расчет электрической цепи в ряде случаев может быть упрощен, если в ней заменить группу сопротивлений, соединенных звездой эквивалентным треугольником или наоборот.

Формулы преобразования звезды в эквивалентный треугольник имеют вид

R ab

= R a

+ R b

+ R a R b ,

R c

R bc

= R b

+ R c

+ R b R c ,

R a

R ac

= R a

+ R c

+ R a R c . (2.60)

R b

Для обратного преобразования треугольника в эквивалентную звезду используют формулы

R = R ab R ac

, R =

R ab R bc

, R =

R ac R bc

. (2.61)

R ab

+ R bc

+ R ac

R ab

+ R bc

+ R ac

R ab

+ R bc

+ R ac

Примечание – Преобразования, определяемые формулами (2.60) и (2.61), являются эквивалентными в том смысле, что при одинаковых значениях потенциалов одноименных точек « a », « b » и « c » треугольника и звезды (рисунок 2.26) подтекающие к этим точкам токи в обеих схемах также одинаковы.

2.8.2 Преобразование параллельного соединения ветвей с источниками ЭДС и источниками тока

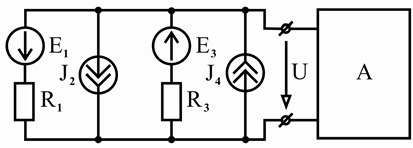
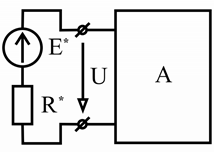
Если в сложной электрической цепи имеются одна или несколько групп параллельно соединенных ветвей с источниками ЭДС и источниками тока (рисунок 2.27, а), то анализ такой цепи можно значительно облегчить путем замены

каждой группы параллельных ветвей одним источником с эквивалентной ЭДС E * и

эквивалентным внутренним сопротивлением

R * (рисунок 2.27, б).

а) б)

Рисунок 2.27 – Замена группы параллельных ветвей (а) эквивалентным источником ЭДС (б)

Параметры E *

формулам

и R * эквивалентного источника ЭДС рассчитываются согласно

m p

åE k g k +åJ k

g * å k g *

E * =

k =1

k =1 ,

g * =

g ,

k =1

R * =

1 , (2.62)

где

g k = 1 R k

( k = 1,n ) — проводимости ветвей с сопротивлениями

R k .

Примечание – В формулах (2.62) со знаком «+» берутся те ЭДС E k

и те токи

источников

J k , которые направлены к тому же узлу, что и эквивалентная ЭДС

E * . В

противном случае ЭДС E k

и токи J k

берутся со знаком «–».

Для группы параллельных ветвей, изображенных на рисунке 2.27, а, эквивалентная ЭДС равна:

E * = - E1g1 - J2 + E3g3 + J4 ,

g *

g * = g

+ g3 .

2.8.3 Преобразование последовательного и параллельного соединения источников энергии

Последовательно соединенные источники ЭДС (рисунок 2.28, а) можно заменить

одним эквивалентным источником с ЭДС

E =åE k . (2.63)

k =1

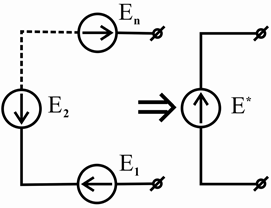
а) б)

Рисунок 2.28 – Замена последовательного соединения источников ЭДС (а) и параллельного соединения источников тока (б) эквивалентными источниками

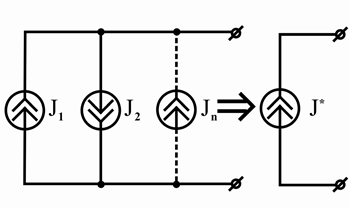
Параллельно соединенные источники тока (рисунок 2.28, б) также можно заменить одним эквивалентным источником с током

Примечания

J =åJ k . (2.64)

k =1

1 Выбор знаков у ЭДС E k

и токов источников J k

в формулах (2.63) и (2.64)

производится по тому же правилу, что и в формулах (2.62), т.е. при совпадении

направлений E k

и J k

с направлениями соответствующих эквивалентных ЭДС E * и

токов J *

эти величины берутся со знаком «+»; при несовпадении указанных

направлений — со знаком «–».

2 Последовательное соединение различных источников тока, а также параллельное соединение различных источников ЭДС недопустимо в схемах замещения электрических цепей, так как противоречит законам Кирхгофа. По этой же причине не допускаются соединения, приводящие к схемам с контурами только из источников ЭДС, и с узлами, в которых сходятся ветви только от источников тока.

2.9 Основные свойства линейных электрических цепей

Основными свойствам линейных электрических цепей являются: принцип наложения (суперпозиции), принцип взаимности и принцип компенсации.

2.9.1 Принцип наложения

Для всех линейных электрических цепей выполняется принцип наложения (суперпозиции): ток в любой ветви электрической цепи равен алгебраической сумме токов в этой ветви, создаваемых каждой из ЭДС схемы в отдельности.

В математической форме принцип наложения следует из формулы расчета контурного тока (2.39). В этой формуле каждую из контурных ЭДС можно выразить

через ЭДС ветвей

E1 ,

E2 , … ,

E k , сгруппировав коэффициенты при этих ЭДС.

Уравнение для расчета тока в любой ветви (например k ) линейной электрической цепи тогда можно записать в виде:

I k = E1g k1 + E2 g k 2 +K+ E k g kk +K+ E n g kn , (2.65)

где

g kk

— собственная (входная) проводимость ветви k ,

g km

— взаимная

проводимость ветвей k и m ( m = 1,n ).

Входная проводимость

g kk

любой ветви k определяется отношением тока I k к

ЭДС E k

в этой ветви при равных нулю ЭДС в остальных ветвях, взаимная

проводимость

g km

двух любых ветвей k и m определяется отношением тока I k

в одной

ветви к ЭДС E m

в другой ветви при равных нулю ЭДС в остальных ветвях:

Примечания

g = I k ,

I k

g =

. (2.66)

1 Собственная проводимость ветви

g kk

имеет положительное значение при

условии, что положительные направления тока и ЭДС в этой ветви совпадают.

2 Взаимная проводимость двух ветвей

отрицательное значение, причем

g km

может иметь положительное или

g km = g mk , (2.67)

что означает выполнение принципа взаимности. Взаимная проводимость отрицательная,

если при выбранном положительном направлении частичного тока I k

в ветви k его

численное значение получается отрицательным (действительное направление тока противоположно положительному).

2.9.2 Принцип взаимности

Принцип взаимности формулируется следующим образом: если ЭДС

E k ,

действующая в ветви k электрической цепи, вызывает ток I m

в другой ветви m этой

цепи, то при отсутствии других источников та же ЭДС вторую ветвь m , вызовет в первой ветви k такой же ток

E k , будучи перенесенной во

I m .

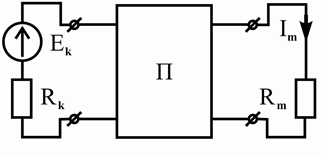
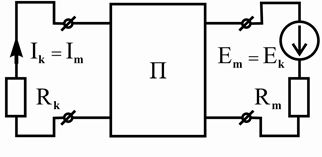
Рисунок 2.29 – Схемы, иллюстрирующие принцип взаимности

Наглядно применение принципа взаимности демонстрируют схемы, изображенные на рисунке 2.29; математическое выражение принципа взаимности задает формула (2.67).

2.9.3 Принцип компенсации

Различают принцип компенсации напряжения и принцип компенсации тока.

Принцип компенсации напряжения заключается в том, что сопротивление R в любой ветви электрической цепи можно заменить идеальным источником ЭДС,

величина ЭДС E которого равна падению напряжения U = IR на этом сопротивлении,

а направление ее действия противоположно направлению тока I в сопротивлении.

Принцип компенсации тока заключается в том, что сопротивление R в любой ветви электрической цепи можно заменить идеальным источником тока, величина задающего тока J которого равна току I в этом сопротивлении, а направление его действия совпадает с направлением тока I в сопротивлении.

Наглядно применение принципа компенсации напряжения демонстрируют схемы, изображенные на рисунках 2.30, а и 2.30, б; принципа компенсации тока — схемы на рисунках 2.30, а и 2.30, в.

а) б) в)

Рисунок 2.30 – Применение к исходной схеме (а) принципа компенсации напряжения (б)

и принципа компенсации тока (в)

Примечание – Принцип компенсации в отношении части схемы, не подвергающейся изменению, является эквивалентным преобразованием, так как его применение к какой-либо ветви цепи не вызывает изменения распределения токов во всех остальных ветвях этой же цепи.

Дата добавления: 2019-07-15; просмотров: 579; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!