Данную формулу называют обычно формулой Муавра.
Пусть n Î N и n >1. Корнем n-й степени из комплексного числа z называется комплексное число a, такое, что a n = z .
Теорема 6.5. (формула корней из комплексного числа)
Для любого ненулевого комплексного числа z = r ( cos φ + isin φ ), где r = | z |, φ = Argz, существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле
, k Î{0, 1, …, n -1}, 
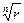– арифметическое значение корня n-й степени из числа r.
Задачи для самостоятельной работы
1. Выясните, образует ли поле следующее множество относительно указанной операции:
а) множество всех матриц вида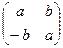 
, где а, b Î Q относительно сложения и умножения матриц;
б) множество чисел вида а + b 
, с целыми а и b относительно сложения и умножения чисел;
в) множество пар (а, b) рациональных чисел относительно бинарных алгебраических операций, заданных по следующим правилам: (а,b) + (с, d ) = (а+с, b+ d ); (а,b) · (с, d ) = (ас+2b d ; а d +bс).
2. Докажите, что алгебраическая система – множество Q рациональных чисел с обычной операцией сложения и операцией ◦, выполняемой по правилу а ◦ в = 
для (" а, в Î Q ) – является полем. Каков единичный элемент этого поля?
3. На множестве М = {а, в} сложение Å и умножение Ä определены следующим образом:
а Å а = а, а Å в = в Å а = в, в Å в = а,
а Ä а = а, а Ä в = в Ä а = а, в Ä в = в.
Выясните, обладает ли это множество нулем и единицей и является ли система (М, Å , Ä ) полем относительно заданных бинарных операций.
|
|
|
4. Будет ли множество чисел вида r 1 + r 2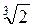 
, где r 1 , r 2 – рациональные числа подполем поля действительных чисел?
5. Пусть множество А состоит из чисел А = {0, 1} и пусть операция сложения на А определяется правилом:
0, если а = в
а + в = 1, если а ¹ в,
а умножение обычным образом. Доказать, что множество А является полем относительно указанных операций.
6. Докажите, что Z[i]={a + bi| а, b Î Z} – наименьшее подкольцо поля комплексных чисел, содержащее все целые числа и число i (кольцо Z[i] называется кольцом целых гауссовых чисел). Укажите кольцо матриц, изоморфное данному кольцу.
7. Любое подполе поля комплексных чисел называется числовым полем. Докажите, что любое числовое поле содержит все рациональные числа.
8. Любое подкольцо поля комплексных чисел называется числовым кольцом. Докажите, что любое числовое кольцо содержит все целые числа.
Векторные пространства
Векторные пространства также считают алгебраической структурой, хотя они и не подходят формально под обычное определение алгебраической структуры, которое было дано в параграфе 1 главы 2.
Пусть V и Р – произвольные непустые множества, Р 
V – прямое произведение этих множеств. Отображение Р V 
V называют внешней бинарной алгебраической операцией, определенной на множестве V над множеством Р.
|
|
|
Пусть дано произвольное поле Р, например, поле рациональных, действительных или комплексных чисел и V – некоторое непустое множество.
Пусть в множестве V задана бинарная алгебраическая операция сложения элементов и внешняя бинарная операция умножения их на числа из P: операция сложения элементов каждой паре а, b Î V ставит во взаимно однозначное соответствие элемент а + b Î V, называемый суммой элементов а и b; операция умножения элементов из множества V на элементы из поля Р каждому элементу а Î V и каждому элементу α из Р ставит во взаимно однозначное соответствие элемент αа из V, называемый произведением элемента а на α.
Непустое множество V называется векторным (или линейным) пространством над полем Р, если в V задана бинарная алгебраическая операция сложение, задана внешняя бинарная алгебраическая операция умножения элементов из Р на элементы из V и при этом выполняются следующие условия (аксиомы):
1. 
– абелева группа;
2. 
;
3. 
;
4. 
;
5. 
.
Элементы множества V называют векторами, элементы поля Р – скалярами, векторное пространство V над полем обозначают символом 
.
|
|
|
Примерывекторных пространств:
1. Рассмотрим множество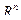 
={ 
} всех n-мерных векторов над полем 
. На этом множестве зададим операции сложения векторов и умножения векторов на скаляр 
следующим образом:
;
.
Легко проверить, что 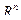с введенными операциями является векторным пространством над полем . Это пространство называют арифметическим векторным пространством.
2. Множество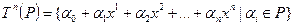 
многочленов степени не выше 
с коэффициентами из поля 
также является векторным пространством над полем P, если операции сложения многочленов и умножения многочленов на скаляр 
задать так:
.
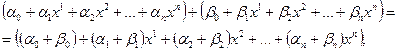
Свойства векторных пространств:
1) 
Доказательство. Рассмотрим верное равенство: 
.
Умножаем обе части равенства на 
: 
.
Прибавляем к обеим частям равенства элемент –( 
) и получаем: 
2) 
.
3) Если 
, то 
.
Доказательство. Имеем: .
Если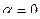 
, тогда условие выполнено.
Если 
, то для него существует обратный элемент из поля . Умножим правую и левую часть равенства на обратный элемент: 
4) Разностью векторов а и b называется вектор 
такой, что 
. При этом пишут: c = а – b , операцию по нахождению разности называют вычитанием.
|
|
|
Разность векторов а и b существует и определена однозначно.
5) а) 
;
б) 
.
Доказательство. а) Докажем это свойство по определению разности, то есть докажем, что 
.
Рассмотрим верное равенство: 
. Умножив правую и левую часть данного равенства на вектор 
, получаем требуемое равенство: .
6) Следующие свойства называют правилами знаков:
a)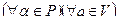 
;
б)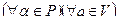 
;
c)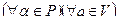 
.
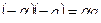Для векторных пространств очень важны понятия линейно зависимой и независимой системы векторов, базиса и размерности.
Пусть 
– система векторов векторного пространства V над полем Р.
Вектор b называют линейной комбинацией векторов 
, если существуют 
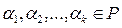такие, что 
В этом случае говорят также, что вектор b линейно выражается через систему векторов .
Линейная комбинация векторов называется тривиальной, если все скаляры 
нулевые.
Система векторов называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору 
.
Система векторов называется линейно независимой, если только тривиальная линейная комбинация этих векторов равна вектору .
Свойства линейной зависимости
1) Система из одного вектора линейно зависима тогда и только тогда, когда вектор нулевой.
2) Система, состоящая из двух векторов а и b является линейно зависимой тогда и только тогда, когда один из векторов линейно выражается через второй.
3) Система векторов является линейно зависимой тогда и только тогда, когда существует вектор этой системы, который линейно выражается через остальные.
Это свойство называют также критерием линейной зависимости системы векторов.
4) Если система векторов является линейно независимой, то и любая её подсистема является линейно независимой.
5) Если подсистема системы векторов является линейно зависимой, то и сама система векторов является линейно зависимой.
6) Если все векторы системы линейно выражаются через векторы системы 
и k>s, то система 
является линейно зависимой.
Это свойство называют также основной теоремой о линейной зависимости.
7) Ступенчатая система векторов является линейно независимой.
Ступенчатой называют систему векторов вида:
a 
= (x 
,x 
,x 
…,x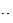 
),
a 
= (0 ,x 
,x 
…,x 
),
a 
= (0, 0 , x 
…,x ),
. . . .
a = (0,0, 0, …, x 
,…, x 
),
где x 
0 для всех i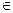 
{1,2,…, r }.
Пример1. По виду системы векторов определить, зависима она или нет:
а) a = (2,1,3) ; б) 
; в) 
; г) 
;
д) a = (2,1,0), a 
= (0,-1,5), a 
= (0,0,6).
Решение.
а) Система линейно независима, так как вектор ненулевой;
б) система линейно зависима, так как подсистема системы 
линейно зависима;
в) система линейно зависима, так как содержит нулевой вектор;
г) система линейно зависима, так как третий вектор системы линейно выражаются через систему векторов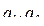 
;
д) система линейно независима, так как система ступенчатая.
Базисом системы векторов векторного пространства называется линейно независимая подсистема этой системы, через которую линейно выражаются все векторы этой системы.
Рангом системы векторов векторного пространства называется число векторов в базисе этой системы векторов.
Пример 2. Найдем базис и ранг системы векторов 
, 
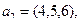
арифметического векторного пространства 
.
Выясним сначала, является ли система векторов линейно независимой. Для этого выясним, существует ли нетривиальная линейная комбинация 
этих векторов, равная нулевому вектору. Решив уравнение = , получаем, что такая линейная комбинация есть: к примеру, верно равенство 
. Поэтому система из трех векторов линейно зависима. Система из векторов 
является линейно независимой (в этом легко убедиться) и через нее можно выразить все три вектора системы: 
, 
, 
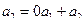. Поэтому система является базисом системы 
и ранг системы векторов равен двум.
Размерность и базис векторного пространства
Векторное пространство V над полем Р называется n-мерным, если в этом векторном пространстве можно найти хотя бы одну линейно независимую систему из n векторов, а любая система, состоящая из большего числа векторов, является линейно зависимой. В этом случае говорят, что размерность V над полем Р равна n и пишут: dim 
= n.
Отдельно дается определение для нулевого пространства (состоит из одного вектора ). Считается, что размерность такого пространства равна нулю.
Пример 3. Покажем,что система векторов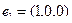 
, 
арифметического векторного пространства является базисом этого векторного пространства.
Эта система является линейно независимой системой (она ступенчатая). Любой вектор 
можно выразить через эту систему следующим образом: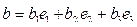 
, поэтому, если мы возьмем систему векторов (S), состоящую из четырех или более векторов, то векторы этой системы линейно выражаются через систему, состоящую из векторов 
. Это означает, что система (S) являетсялинейно зависимой системой и dim 
= 3.
Если векторное пространство является n-мерным, то его также называют конечномерным.
Базисом конечномерного векторного пространства называется линейно независимая система векторов этого пространства, через которую линейно выражаются все векторы пространства.
Теорема 7 .1. Если в конечномерном пространстве существует базис из n векторов, то размерность пространства равна n.
Доказательство. Пусть система (S) состоящая из векторов 
– базис векторного пространства.
Возьмем произвольную систему (T): 
, где s > n. Все векторы системы (T) можно выразить через базис – систему (S), поэтому система (T) является линейно зависимой (по основной теореме о линейной зависимости).
По определению имеем: размерность векторного пространства равна n.
Теорема 7 .2. В n-мерном пространстве любая линейно независимая система из n векторов является базисом.
Замечание. Теорема 7.2 значительно облегчает решение задачи о том, является ли некоторая система векторов базисом некоторого пространства, в случае, если известна размерность этого пространства.
Пример 3. Выясним, является ли система векторов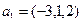 
, 
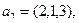
базисом пространства .
Известно, что dim = 3.
Решив уравнение = , получаем, что только тривиальная линейная комбинация этих векторов равна нулевому вектору, то есть система является линейно независимой.
Известно, что dim = 3, поэтому любая линейно независимая система из трех векторов, а значит, и рассматриваемая система, является базисом этого пространства.
Теорема 7 .3. В любых двух базисах конечномерного пространства содержится одинаковое число векторов.
Теорема 7 .4. Любая линейно независимая система векторов конечномерного пространства либо является базисом, либо её можно дополнить до базиса этого пространства.
Непустое подмножество L векторного пространства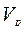 
называется подпространством этого пространства, если оно само является пространством относительно операций, заданных в пространстве .
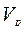Критерий подпространства:
Непустое подмножество L векторного пространства 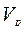является подпространством этого пространстватогда и только тогда, когда:
1) ( " a,b Î L) a+b Î L; 2) ( " 
Î P) ( " a Î L) 
a Î L.
Примеры подпространств:
1. Рассмотрим множество L ={ 
} всех n-мерных векторов над полем , у которых первая и вторая координаты равны.
Легко проверить, что L является подпространством арифметического векторного пространства .
2. Множество L = 
многочленов степени не выше n с нулевым свободным членом является подпространством пространства многочленов степени не выше n с коэффициентами из поля 
.
Дата добавления: 2019-02-12; просмотров: 295; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!