Для ответа на поставленный вопрос введем следующее определение.

Будем называть полем комплексных чисел любое поле С, для которого выполняются три условия:

а) поле С является расширением поля действительных чисел;

б) некоторый элемент поля С удовлетворяет уравнению х²+ 1 = 0, где 1 и 0 – нейтральные элементы поля относительно умножения и сложения;

В) любое подполе поля С, удовлетворяющее условиям а) и б) совпадает с полем С.

Построим некоторое конкретное поле комплексных чисел и тем самым убедимся, что такие поля существуют. В качестве множества С возьмем множество R´R=R² – декартов квадрат множества действительных чисел. Элементами этого множества являются всевозможные упорядоченные пары (a; b) действительных чисел. Определим на этом множестве операции сложения и умножения его элементов следующим образом:

1. (a; b) + (c; d) = (a + c; b + d);

2. (a; b) · (c; d) = (ac - bd; bc + ad).

Можно показать, что (R², +, ·) – поле.

Построенное поле (R², +, ·) является полем комплексных чисел, а его элементы – упорядоченные пары действительных чисел, называются комплексными числами.

Пусть i =(0; 1). Существует элемент i (мнимая единица) такой, что i²= i × i =(0; 1) × (0; 1) = – 1. Итак, i²=–1. Тогда (" (a; b) Î С ) (a; b)= (a; 0)+ (0; b)= (a; 0)+(0; 1) × ( b; 0)= a + bi.

Название «мнимые числа» было введено французским математиком и философом Р. Декартом в 1637 году. А в 1777 году один из крупнейших алгебраистов XVIII века, Леонард Эйлер предложил использовать первую букву французского слова «imaginaire» (мнимый) для обозначения числа i ( i ² =-1).

Символ a + bi называют алгебраической формой комплексного числа с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части. При этом пишут: Re z = a; Im z = b.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a+0i=a. Числа вида bi (b ¹ 0) называют чисто мнимыми.

Например, комплексное число 3–4i имеет действительную часть – действительное число 3 и мнимую часть – 4i, действительное число – 4 – коэффициент мнимой части.

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d. И, обратно, если a = c, b = d, то a + bi = c +di.

Рассмотрим операции над комплексными числами в алгебраической форме:

а) правило сложения и вычитания комплексных чисел:

(a + bi) + (c + di) = (a + c) + (b + d)i.

Например: (-3 + 4i) + (6 + i) = (-3 + 6) + (4 + 1)i = 3 + 5i;

Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:

(a + bi) – (c + di) = (a – c) + (b – d)i.

Например:

(6 – 2i) – (3 – 2i) = (6 – 3) + ((– 2) – (– 2))i = 3 + 0i = 3.

б) правило умножения комплексных чисел:

(a + bi)(c + di) = (a с + bd) + (ad + bc)i.

Операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i² = – 1.

Действительно: (a + bi)(c + di) = ac + adi + bdi² = (ac – bd) + (ad + bc)i.

Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i² = – 2 – 5i + 6i – 15 = – 17 + i;

(2 + 3i)(2 – 3i) = 4 – 6i + 6i – 9 i² = 4 + 9 = 13.

Из приведенного примера следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:

(a + bi)(a – bi) = a² – abi + abi – b²i² = a² + b².

Произведение двух чисто мнимых чисел – действительное число.

в) Деление комплексного числа a + bi на комплексное число c+di ¹ 0 определяется как операция обратная умножению и выполняется по формуле:

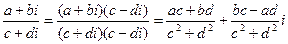
Формула не имеет смысл, если c+di=0, так как тогда c² + d² = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.

Комплексная плоскость С – плоскость с прямоугольной декартовой системой координат х, у, каждая точка которой (х; у) отождествлена с комплексным числом z =х+ yi . Поэтому на комплексной плоскости говорят о точках z или о векторах z , подразумевая вектор, приложенный в начале координат с концом в точке z . Ось абсцисс ОХ на комплексной плоскости называется действительной осью, а ось ординат OY – мнимой осью.

Модулем комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости.

Модуль комплексного числа z =х+ yi обозначается | z | и определяется выражением . Часто модуль обозначается символом r. Если z является вещественным числом, то | z | совпадает с абсолютной величиной этого вещественного числа.

Аргументом комплексного числа называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке.

Аргумент комплексного числа обычно обозначается символами

φ или arg z.

Из определения следует, что для ненулевого комплексного числа z =х+ yi выполняются равенства: cos φ = 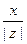; sin φ = .

Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до 2 n, где n — любое целое число.

Главным значением аргумента называется такое значение φ, что - π < φ ≤ π.

С помощью введенных понятий можно перейти от алгебраической к тригонометрической форме комплексного числа.

Пусть z =х+ yi 0. Тогда |z |= r 0. Запишемкомплексное число следующим образом: z = х+ yi = r ( + )= r ( cos φ + isin φ ).

Тригонометрической формой комплексного числаz называется выражение вида z = r ( cos φ + isin φ ), где r – модуль комплексного числа z ; φ =А rg z – главный аргумент комплексного числа z , - π < φ ≤ π .

Теорема 6.1. (об умножении и делении комплексных чисел в тригонометрической форме).

Для комплексных чисел z₁=r₁ (cosφ₁+isinφ₁) и z₂=r₂ (cosφ₂+isinφ₂) справедливы равенства:

z₁z₂=r₁r₂ (cos(φ₁+φ₂)+isin(φ₁+φ₂)) (произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей и аргумент – сумме аргументов сомножителей);

Теорема 6.4. (о возведении комплексного числа в степень)

Для n-ой степени числа z=r(cosφ+isinφ) справедливо равенство:

zⁿ=rⁿ (cos(nφ)+isin(nφ)), nÎZ.

Дата добавления: 2019-02-12; просмотров: 314; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!