Задачи для самостоятельной работы
1. Являются ли гомоморфизмами следующие отображения одной группы в другую?
а) ( R , +)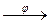 
( Z , +), j (а)=[а];
б) ( R , +) 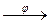( R *, × ), j (а) = 1 ;
в) ( R + , × ) 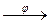( R , +), j (а) = log 2 a ;
г) ( R \{0}, × ) 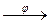( R + , × ), j (х)=½х½.
2. Является ли данное отображение х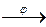 
3х изоморфизмом аддитивной группы действительных чисел на мультипликативную группу положительных действительных чисел: ( R , +) → ( R + , ∙)?
3. Для каких групп действительных чисел отображения:
а) f ( x ) =3 x ; б) g ( x ) = x 3 являются автоморфизмами?
4. Покажите, что мультипликативная группа положительных рациональных чисел неизоморфна аддитивной группе рациональных чисел.
5. Докажите, что всякая группа изоморфна самой себе.
6. Докажите, что аддитивная группа целых чисел изоморфна любой своей ненулевой подгруппе.
Кольца. Основные свойства колец
Алгебра (К, +, ∙) – кольцо, если:
1. (К, +) – абелева группа.
2. (К, ∙ ) – полугруппа.
3. Умножение дистрибутивно относительно сложения.
В развернутом виде определение кольца таково:
Алгебра (К, +, ∙) – кольцо, если:
1. ( " a, b Î K) a+b Î K, a·b Î K;
2. ( " a, b, c Î K) a+(b+c) = (a+b)+c;
3. ( " a, b Î K ) a+b = b+a;
4. ( $ n Î K) ( " a Î K) a+n = n+a = a;
5. ( " a Î K) ( $ a´ Î K) a+a´=a´+a = n;
6. ( " a, b, c Î K) a·(b·c) = (a·b)·c;
7. ( " a, b, c Î K) (a+b)·c = ac+bc, c·(a+b) = ca+cb.
Кольцо с единицей (т.е. нейтральным элементом относительно умножения) называется кольцом с единицей или унитарным кольцом. Если умножение коммутативно, то кольцо называется коммутативным.
|
|
|
Примеры колец:
1. (Z, +, ·), (Q, +, ·) (R, +, ·) – коммутативные кольца с единицей.
2. На множестве Z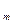 
={ 
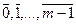} классов-вычетов по модулю m зададим операции сложения и умножения классов-вычетов.
Суммой (произведением) классов-вычетов, порожденных элементами a и b , назовем класс вычетов, порожденный элементом a + b ( ab ). С помощью свойств отношения сравнения легко показать, что сумма и произведение классов-вычетов не зависят от выбора элементов, порождающих класс.
(Z 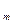, +, ·) – коммутативное кольцо с единицей, которое называют кольцом классов-вычетов.
Свойства колец:
I. Так как (К, +) – абелева группа, то справедливы все свойства групп.
II. Характеристические свойства:
1. 0 ∙ а = а ∙ 0 = 0 (нуль является поглощающим элементом).
Доказательство. Прибавим к элементу 0∙а элемент а и воспользуемся аксиомами кольца:
0 ∙ а + а = 0 ∙ а+1 ∙ а = (0+1) ∙ а=1 ∙ а = а=0 + а.
Таким образом имеем равенство: 0∙а + а = 0 + а. Так как кольцо К относительно операции сложения является группой, то справедлив закон сокращения и, применяя его сразу, получаем равенство 0 ∙ а = а.
2. Правило знаков: (-а)∙ b = -(а∙ b ); а∙(- b ) = -(а∙ b ); (-а) ∙ (- b ) = а∙ b .
|
|
|
3.( " a , b Î К) а∙( b - с)=а b – ас дистрибутивность умножения
( b - с) ∙ а = b а –са относительно вычитания
Пусть К – коммутативное кольцо с единицей. В кольце К можно определить отношение делимости следующим образом:
а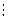 
b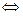 
$ q Î K, что а = b · q .
Элемент ε кольца К называется обратимым, если в кольце К существует такой элемент ε1, что ε · ε1 = е.
Свойство: а 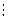b 
ε – обратим в кольце К Þ а 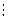b ε.
Элементы а и b кольца К называются делителями нуля, если а ¹ 0 и b ¹ 0, но а· b = 0.
Коммутативное унитарное кольцо К без делителей нуля называют областью целостности.
Областью целостности являются, например, кольцо целых чисел Z, а также кольцо многочленов над произвольным полем.
Пример 1. Кольцо функций F[0, 1], определенных на отрезке [0; 1], является коммутативным унитарным кольцом с единицей, которое имеет делители нуля. Например, положим
f ( x )=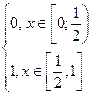 
, g ( x )= 
.
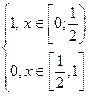Тогда f(x) и g(x) – ненулевые функции, определенные на отрезке [0; 1], т.е. являются элементами кольца F[0, 1] . Найдем их произведение, которое равно нулевой функции: f(x) × g(x)= 0(x).
Пример 2. Кольца (Z, +, ·), (Q, +, ·) (R, +, ·) являются областью целостности.
Элементы кольца называются ассоциированными, если а b
|
|
|
b а.
Пусть имеется два кольца (К1, +, ∙) и (К2, 
).
Отображение ƒ: К1 ® К2 называется гомоморфизмом колец, если:
1) ƒ(а+ b )=ƒ(а)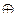 
ƒ( b ); 2) ƒ(а· b ) = ƒ(а) 
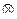ƒ( b ).
Гомоморфное биективное отображение кольца К1 на кольцо К2 называют изоморфизмом колец.
Так как кольцо относительно первой операции является группой, то для колец справедливы все свойства гомоморфизма групп.
Теорема 5.1. Гомоморфный образ кольца является кольцом.
Множество элементов кольца К1, переходящее при гомоморфизме ƒ в нуль кольца К2, называется ядром гомоморфизма.
Подмножество L кольца К называется подкольцом кольца К, если оно является кольцом относительно операций сложения и умножения, заданных в К. В этом случае кольцо К называется надкольцом L (или расширением кольца К).
Критерий подкольца:
Непустое подмножествоS кольца К является подкольцом тогда и только тогда, когда:
1) ( " а, b Î S ) а + b Î S ; │ или ( " а, b Î S )
2) ( " а Î S ) -а Î S; │ 1) а - b Î S;
3) ( " а, b Î S ) а · b Î S. │ 2) а · b Î S.
Примеры.
1. ( Q , +, ·) – подкольцо кольца ( R , +, ·).
2. ( Z , +, ·) – подкольцо кольца ( Q , +, ·).
Если кольцо К коммутативно, то и любое его подкольцо тоже коммутативно. Но из того, что кольцо К содержит единицу, не следует, что любое подкольцо в К содержит единицу. Например, кольцо целых чисел Z содержит единицу, а его подкольцо, состоящее из четных чисел, не содержит единицы, то есть нейтрального элемента относительно умножения.
|
|
|
Дата добавления: 2019-02-12; просмотров: 184; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!