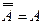Задачи для самостоятельной работы
ВВЕДЕНИЕ
Настоящее учебное пособие подготовлено в соответствии с федеральным государственным образовательным стандартом высшего профессионального образования третьего поколения по направлению подготовки 050100 Педагогическое образование.
Пособие состоит из шести глав, написанных коллективом авторов, которые на протяжении многих лет проводили лекции и практические занятия по вузовским дисциплинам, разделы которых входят в настоящее пособие.
Первая глава содержит основы аксиоматического метода построения математической теории. В данной главе освещены вопросы вводной части математического курса по теме «Множества и отношения».
Во второй главе рассмотрены основные алгебраические структуры: полугруппы, группы, кольца, поля, векторные пространства. Для каждого из этих понятий приведены примеры, указаны свойства и основные теоремы.
Третья, четвертая и пятая главы пособия посвящены применению алгебраических структур при решении систем линейных уравнений, в криптографии, в теории кодирования. При решении прикладных задач часто пользуются элементами каких-то конкретных алгебр. Так, в системах линейных уравнений коэффициенты и свободные члены берут из некоторого поля; для того, чтобы некоторое сообщение в криптографии можно было сначала зашифровать, а потом расшифровать, удобно пользоваться элементами группы; в теории кодирования сообщениями являются элементы векторных пространств.
|
|
|
В шестой главе пособия изложены на ознакомительном уровне ключевые аспекты современной алгебраической геометрии.
Каждая тема начинается с перечисления основных понятий, имеющих к ней непосредственное отношение и являющихся основой для самостоятельной работы студентов. Теоретические сведения подкрепляются многочисленными примерами. В конце тем приводятся задачи для закрепления теоретического материала и самостоятельной работы студентов.
В учебном пособии представлено 10 вариантов индивидуальных заданий по рассматриваемой теме, что способствует активизации самостоятельной работы студентов.
В заключении дается список рекомендуемой литературы по предлагаемым для изучения вопросам с более подробным изложением.
Неотъемлемой частью данного учебного пособия является электронный практикум по теме «Основные алгебраические структуры».
В приложении учебного пособия представлено содержание элективного курса по теме «Основные алгебраические структуры» для учащихся средней школы.
ГЛАВА 1
ВВЕДЕНИЕ В МАТЕМАТИКУ
Аксиоматический метод
Математика – самая древняя наука, которая развивалась вместе с человечеством. Примерно в VI веке до н. э., в Древней Греции, математика приобрела статус самостоятельной науки. Именно это время можно считать началом периода элементарной математики. Постепенно из арифметики выделяется теория чисел и создается алгебра как буквенное исчисление. Система изложения элементарной геометрии, созданная древними греками, на два тысячелетия вперед сделалась образцом дедуктивного построения математической теории. XVII век стал для математики эпохой ее активного развития.
|
|
|
Применение математики Галилеем и Кеплером для исследования движения небесных тел позволили им открыть законы движения планет вокруг Солнца. Научные труды Лейбница, Декарта и Ньютона повлекли за собой новый этап развития математики, а именно появление математики переменных величин. В результате этого начался период дифференциации единой науки математики на ряд самостоятельных наук: алгебру, аналитическую геометрию, математический анализ. В свою очередь, это способствовало интенсивному развитию физики и астрономии.
Новый этап развития математики в начале 19 века придал ей абстрактный характер. Имена Лобачевского и Римана стали достоянием истории. Созданная Кантором на рубеже XIX и XX столетий теория множеств легла в фундамент современной математики.
|
|
|
Потребности развития математики, «математизация» различных областей науки, проникновения математических методов практически во все сферы деятельности человека, информатизация общества и др. привели к появлению ряда современных математических дисциплин таких, например, как математическая экономика, исследование операций, теория игр, компьютерная алгебра и др.
В основе построения математической теории лежит аксиоматический метод, основы которого были заложены в книге Д. Гильберта «Основания геометрии», вышедшей в 1899 году.
Остановимся несколько подробнее на характеристике аксиоматического метода. Всякое понятие, вводимое в математическую теорию, должно быть точно определено. Каждое определение сводит новое понятие к ранее известным. Таким образом, построение всякой теории необходимо начинать с некоторых первичных понятий.
Для того чтобы выделить основные понятия, относительно них высказывают некоторые предложения, называемые аксиомами, в которых устанавливаются отношения между этими понятиями. Слово «аксиома» происходит от греческого «axios» и означает «достойное признания»; прежде и понимали «аксиому» как положение, достойное признания ввиду его очевидности, не требующее доказательства. Указание системы аксиом представляет собой своеобразный способ определения новых понятий. Одной и той же системе аксиом могут удовлетворять различные совокупности объектов. Каждая совокупность объектов, для которой истинна данная система аксиом, называется интерпретацией этой системы.
|
|
|
Всякая система аксиом должна удовлетворять следующим основным требованиям: непротиворечивость, независимость и полнота.
Система аксиом называется непротиворечивой, если, получая из нее различные логические следствия, никогда нельзя вывести одновременно истинность и ложность некоторого утверждения. Чтобы доказать, что данная система аксиом непротиворечива, обычно используют ее интерпретацию, т.е. находят такую совокупность объектов, для которой выполняется данная система аксиом. Система аксиом называется содержательно непротиворечивой, если существует интерпретация этой системы.
Независимость является следующим требованием к системе аксиом. Аксиома называется независимой от остальных аксиом, если она не может быть получена из остальных по логическим правилам. Если все аксиомы аксиоматики независимые, то аксиоматика называется независимой.
Аксиоматическая теория называется полной в широком смысле (абсолютно полной), если средств аксиоматической теории достаточно, чтобы доказать или опровергнуть любое утверждение данной теории. Аксиоматическая теория называется полной в узком смысле, если добавление к ее аксиомам недоказуемого в ней утверждения с сохранением имеющихся логических правил приводит к противоречивости теории.
Всякая отдельная область математики начинает свое построение с выделения некоторого числа своих первичных понятий. Так, основные понятия геометрии – точка, прямая, плоскость и некоторые другие. Основное понятие арифметики – натуральное число.
Первые математические теории побудили ученых систематизировать отдельные факты и изложить последовательно основы математики. Составление первого систематического курса геометрии, который назывался "Элементы" и был основан на аксиомах и определениях, приписывается Гиппократу Хиосскому. Потом, в III в. до н.э., в Александрии с тем же названием появилась книга Евклида, что в переводе на русский язык означает «Начала». От латинского названия «Начал» произошёл термин «элементарная геометрия». Сочинения предшественников Евклида до нас не дошли, однако, несмотря на это, мы можем составить определенное мнение о них по «Началам» Евклида. В «Началах» представлены разделы, логически мало связанные с другими ее разделами. Их появление объясняется только тем, что они внесены по традиции и копируют «Начала» предшественников Евклида.
«Начала» Евклида состоят из тринадцати книг. Первые шесть книг посвящены планиметрии, последующие четыре – арифметике и несоизмеримым величинам, которые можно построить с помощью циркуля и линейки. Книги с одиннадцатой по тринадцатой представлено изложение стереометрии.
«Начала» начинаются с изложения двадцати трех определений и десяти аксиом. Первые пять аксиом – «общие понятия», являются принципами измерения длин, углов, площадей, объёмов: «равные одному и тому же равны между собой», «если к равным прибавить равные, суммы равны между собой», «если от равных отнять равные, остатки равны между собой», «совмещающиеся друг с другом равны между собой», «целое больше части».
Последующие пять аксиом "Начала" называются «постулатами». Действия с помощью идеальной линейки определяют первые два постулата, с помощью идеального циркуля - третий постулат. Излишним является четвёртый постулат («все прямые углы равны между собой»), поскольку его можно вывести из остальных аксиом. Пятый, последний постулат утверждает: «Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то, при неограниченном продолжении этих двух прямых, они пересекутся с той стороны, где углы меньше двух прямых».
Далее началась критика геометрии Евклида за то, что он рассматривал только геометрические величины, которые можно построить с помощью циркуля и линейки; за то, что он разрывал арифметику и геометрию, доказывая для целых чисел то, что уже доказал для геометрических величин, и, наконец, за его аксиомы. Очень сильной критике подвергся пятый постулат, самый сложный постулат Евклида. Большинство ученых считали его лишним, и что его необходимо вывести из других аксиом. Другие предлагали заменить его более простым, равносильным ему: «Через точку вне прямой можно провести в их плоскости не более одной прямой, не пересекающей данную прямую».
Критика разрыва между арифметикой и геометрией повлекла за собой расширение понятия числа до действительного числа. Споры о пятом постулате Евклида привели к тому, что в начале XIX века Н. И. Лобачевский, К. Ф. Гаусс и Я. Бойяи построили новую геометрию, в которой выполнялись все аксиомы геометрии Евклида, за исключением пятого постулата, замененного противоположным утверждением: «В плоскости через точку вне прямой можно провести более одной прямой, не пересекающей данную».
Французским математиком Анри Пуанкаре в 1882 году была построена модель планиметрии Лобачевского на евклидовой плоскости. Все аксиомы планиметрии Лобачевского непротиворечивы.
За геометрией Лобачевского появились другие непротиворечивые геометрии: от евклидовой отделилась проективная геометрия, возникла многомерная евклидова геометрия, появилась риманова геометрия и др.
Основным методом в математических исследованиях являются математические доказательства – строгие логические рассуждения, без которых математика немыслима.
В настоящее время на первый план выходит математическая модель, которую можно определить как внутренне непротиворечивую замкнутую систему математических соотношений, предназначенную для воспроизведения определенного качества (или группы определенных качеств) изучаемого реального явления или процесса. Одна и та же математическая модель может описывать свойства различных друг от друга по своему конкретному содержанию реальных явлений. Однако для математики важна не природа рассматриваемых объектов, а существующие между ними отношения.
В математике используется два вида умозаключений: дедукция и индукция. Дедукция позволяет сделать вывод на основании общих знаний для конкретного случая, а индукция, наоборот – на основании частных случаев сделать вывод об общих суждениях.
Принцип математической индукции состоит в том, что утверждение А( n ), зависящее от натурального параметра n, считается доказанным, если доказано А(1) и для любого натурального числа n из предположения, что верно А( n ), доказано, что верно также А( n +1).
При формулировке математических утверждений используются необходимые и достаточные условия.
Необходимыми условиями истинности утверждения А называются условия, без соблюдения которых А не может быть истинным.
Достаточными условиями называются такие условия, при наличии (выполнении, соблюдении) которых утверждение А является истинным.
Утверждение А является необходимыми достаточным условием утверждения B, когда A является как необходимым условием B, так и достаточным. В этом случае говорят ещё что A и B равносильны или эквивалентны.
Множества и отношения
В основе многих разделов классической математики лежит теория множеств. Множество является первичным понятием в математике и, следовательно, неопределяемым. Понятие «множество» можно раскрыть, воспользовавшись, предложенным академиком Н.Н. Лузиным, образным представлением его в виде прозрачной непроницаемой оболочки, внутри которой заключены все элементы данного множества.
Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое.
Существует два основных способа задания множеств: перечисление и описание с помощью характеристического свойства.
Пусть X – множество. Запись хÎХ означает, что элемент х принадлежит множеству X. Запись хÏХ означает, что элемент х не принадлежит множеству X . Множество, не содержащее элементов, называется пустым и обозначается символом Æ.
Множество А называется подмножеством множества X и символически обозначается как A Ì X, если каждый элемент множества А принадлежит множеству X. В этом случае говорят также, что А включено в X.
В математике выделение тех или иных подмножеств данного множества имеет большое значение. Так, например, геометрическая фигура трактуется как подмножество геометрического пространства, множество решений уравнения f ( x )= g ( x ) является подмножеством множества решения уравнения f 2 ( x )= g 2 ( x ) и т.д. В любом множестве А можно всегда указать два подмножества – пустое и само множество А. Эти подмножества называются несобственными подмножествами. У n–элементного множества имеется 2 n подмножеств.
Множества X и Y называются равными (равенство обозначается Х = Y), если они состоят из одних и тех же элементов. Доказательство равенства множеств X и Y можно проводить в два этапа:
1) доказать включение X Ì Y;
2) доказать обратное включение Y Ì X.
Рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества.
Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В: AÈB= 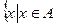
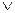
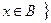 .
.
Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих как множеству А, так и множеству В: AÇB= 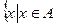 Ù
Ù 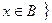 .
.
Разностью множеств А и В называется множество, элементами которого являются элементы множества А, не принадлежащие множеству В: A\B= 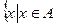 Ù
Ù 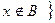 .
.
Если А Ì U, то разность U \А называется дополнением множества А до множества U и обозначается CU А (или 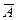 ):
): 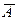 =
= 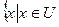 Ù
Ù 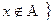 .
.
Для графического изображения множеств и их свойств используются так называемые диаграммы Венна (или круги Эйлера), которые представляют собой схематическое изображение множеств (рис.1).
 |
AÈB A ÇB A A\B
Рис.1. Операции над множествами на кругах Эйлера
Рассмотрим основные свойства операций над множествами:
| Свойства операции объединения | Свойства операции пересечения |
| Свойство коммутативности | |
| 1. AÈB = BÈA | 2. AÇB= BÇA |
| Свойство ассоциативности | |
| 3. ( AÈB ) È C = AÈ(BÈC ) | 4. (AÇB) ÇC=AÇ (BÇC) |
| Дистрибутивный закон | |
| 5. AÇ(BÈС)=( AÇB )È( AÇC ) | 6. AÈ(BÇC)=(AÈB)Ç(AÈC) |
| 7. AÈA=A | 8. AÇA=A |
| 9. AÈÆ=А | 10. AÇÆ=Æ |
| 11. AÈU=U | 12. AÇU= A |
13. AÈ 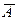 =U =U
| 14. AÇ 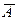 =Æ =Æ
|
| Законы де-Моргана | |
15. 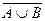 = = 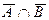
| 16.  = = 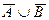
|
| Закон двойного отрицания | |
| 17. | |
Доказательства этих свойств можно провести на основе равенства: A = B Û AÍB Ù BÍA, параллельно используя графическое толкование (круги Эйлера). Например, доказательство дистрибутивного закона (формула 5) оформим следующим образом:
AÇ( BÈC )=( AÇB )È( AÇC )
x Î (AÇ(BÈC)) Þ (x Î A)и x Î (B ÈC) Þ
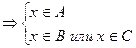 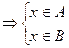 или или 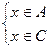 Þ
Þ x Î (AÇB) или x Î (AÇC) Þ
Þ x Î ((AÇB)È(AÇC)) Þ
Þ x Î (AÇB) или x Î (AÇC) Þ
Þ x Î ((AÇB)È(AÇC))
|
AÇ(BÈC)
A B C | |||
x Î ((AÇB)È(AÇC)) Þ x Î (AÇB) или x Î (AÇC) 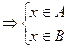 или или 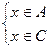 Þ Þ
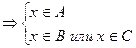 Þ Þ 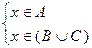 Þ
Þ x Î (AÇ(BÈC)) Þ
Þ x Î (AÇ(BÈC))
|
(AÇB)È(AÇC)
A B С
|
Замечаем, что если в каждом из тождеств (1) – (15) заменить знак Ç на знак È и обратно, то мы получим другое из этих тождеств.
Равенство алгебры множеств, полученное из другого равенства такой заменой, называют двойственным исходному.
Принцип двойственности:
Если тождественно верно некоторое равенство алгебры множеств, сформулированное в терминах Ç, È,  , то тождественно верно и двойственное ему равенство.
, то тождественно верно и двойственное ему равенство.
Одно из основных понятий теории множеств – понятие бинарного отношения. Это понятие играет немаловажную роль в формировании математических знаний, так как изучение математики в значительной мере сводится к изучению отношений.
Определение понятия бинарного отношения введем в следующей логической последовательности:

 множество Þ упорядоченная пара Þ прямое произведение
множество Þ упорядоченная пара Þ прямое произведение
разбиение множества Þ отношение эквивалентности Ü бинарное отношение
Пусть а, b – какие-нибудь объекты. Любым двум объектам а и b поставим в соответствие новый объект – их упорядоченную пару (а, b ). В общем случае, если а ¹ b , то ( a , b ) ¹ ( b , a ). Очевидно, пара ( a , b )=( c , d ) Û a = c Ù b = d.
Из одноэлементного множества {a} можно образовать одну упорядоченную пару ( a , a ), а из двухэлементного множества {a , b} – четыре упорядоченные пары ( a , a ), ( b , b ), ( a , b ) и ( b , a ). Обозначение упорядоченных пар с помощью стрелок будет следующим:
 |  | ||
a – пара (a, a), a b – пара (a, b).
Прямым произведением множеств A и B назовем множество, состоящее из всех упорядоченных пар (а, b ) таких, что а Î A , b Î B . Обозначим: A × B ={(а, b )ïа Î A , b Î B}.Если множества A и B совпадают, то A × A = A 2. Такое произведение называют декартовым квадратом множества A.
Множество всех упорядоченных троек (х, у, z ), где x Î A , y Î B , z Î C, называется прямым или декартовым произведением множеств А, В, С и обозначается А ´ В ´ С. Произведение А ´ А ´ А называется декартовым кубом множества А и обозначается А3. Аналогично определяется декартово (прямое) произведение четырех и более множеств, а также n-я декартова степень Аn множества А.
Пример 1.
Если А=[0,1], то множество А ´ А=А2 на координатной плоскости изобразится заштрихованной частью координатной плоскости (рис.2).
 |
Рис.2. Изображение прямого произведения множеств
Из определения следует, что прямое произведение множеств А и В некоммутативно, т.е. А ´ В ¹ В ´ А.
Любое подмножество ρ прямого произведения А ´ В, где А, В – произвольные множества, называется бинарным отношением между множествами А и В.
Кроме бинарных отношений существуют, например, тернарные отношения, связывающие элементы в упорядоченные тройки, и вообще n -арные отношения, соединяющие элементы в упорядоченные n -ки.
Существуют следующие способы задания бинарных отношений:
1) Если множество М конечно, то отношение r между элементами этого множества задаем перечислением всех пар, принадлежащих отношению r .
2) Отношение r между элементами множества М можно задать, указав характеристическое свойство пар, принадлежащих ему.
3) Словесное задание. Например, «x меньше y».
4) Задать отношение можно при помощи графа, таблицы и графика на координатной плоскости.
При задании бинарного отношения с помощью графа элементы множеств изображают вершинами графа. В случае, если элементы а Î A , b Î B связаны отношением r , соединяем соответствующиеэтим элементам вершины графа ориентированным ребром с началом в а и концом в b .
Пример 2.
а) Бинарным отношением между множествами R и N будет множество ρ ={(0, 2), (-3, 1),(2, 5)};
б) Бинарным отношением между множествами Z и N будет множество ρ ={( a , b ) | a > b )}.
Краткая символическая запись предложения «x находится в отношении r с y»: x r y . С теоретико-множественной точки зрения это означает, что ( x , y ) Î r .
Множества А ´ В, Æ являются подмножествами прямого произведения А ´ В, их соответственно называют полным и пустым отношением.
Множество первых элементов пар (а, b ) Î ρ называется областью определения этого отношения и обозначается символом Dom ρ: Dom ρ={a | $ b , (а, b ) Î r}.
Множество всех вторых элементов пар (а, b ) Î ρ называется областью значения отношения ρ и обозначается символом Im ρ: Im ρ ={b | $ a , (а, b ) Î r}.
Если А=В, то ρ Î А ´ А называется отношением на множестве А.
Пример 3.
1. Отношение «меньше» на множестве Z: ρ ={( a , b ) | a < b )}.
2. Отношение делимости на множестве Z: (аρ b ) Û (а  b ).
b ).
Бинарные отношения называются равными, если они равны как множества.
По некоторым важным свойствам бинарные отношения делятся на виды.
Отношение r на множестве М называется рефлексивным, если для любого x Î М пара ( x , x ) Îr, то есть для всякого x Î М верно x r x .
Примером рефлексивных отношений является отношение равенства на любом множестве, отношение параллельности на множестве прямых плоскости.
Граф рефлексивного отношения во всех точках, изображающих элементы множества М, имеет петли (рис. 3, а).
 | |||||
 | |||||
 | |||||

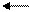
 x x y x z y
x x y x z y
а) б) в)
Рис. 3. Графы отношений
Отношение r называют антирефлексивным на множестве М, если ни для какого элемента x из М не выполняется отношение x r x. Или, антирефлексивное отношение – это отношение, не содержащее ни одной пары вида (x, x).
Например, отношение перпендикулярности на множестве прямых плоскости является антирефлексивным.
Граф, соответствующий антирефлексивному отношению, не имеет ни одной петли.
Отношение r называется симметричным на множестве М, если для каждой пары элементов множества М из того, что x r y следует y r x.
Например, отношение параллельности на множестве прямых плоскости симметрично. Граф симметричного отношения вместе с каждой стрелкой из точки x в точку y должен содержать стрелку, соединяющую те же точки, но в обратном направлении (рис. 3, б).
Отношение r в М называется антисимметричным, если x r y и y r x одновременно выполняется в том и только том случае, когда x = y . Например, отношение «меньше» на множестве целых чисел антисимметрично.
Отношение r называется транзитивным на множестве М, если для любых трех элементов x , y , z Î М из того, что x r y и y r z следует x r z . Граф транзитивного отношения изображен на рис.3, в).
Отношение, обладающее свойством рефлективности, симметричности и транзитивности, называется отношением эквивалентности.
С понятием отношения эквивалентности связаны понятия класса эквивалентности и фактор-множества.
Пусть r –отношение эквивалентности, заданное на множестве М, а 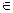 М.
М.
Классом эквивалентности, порожденным элементом а, называется множество элементов множества М, находящихся в отношении r с элементом a .
При этом пишут:  = {
= { 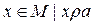 }.
}.
Множество всех классов эквивалентности множества М по отношению эквивалентности r называется фактор-множеством.
В этом случае пишут так: М / r = {  ,
, 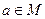 }.
}.
Отношение эквивалентности является одним из важных и часто встречающихся типов отношений между объектами различной природы. Важность этого отношения объясняется его связью с понятием разбиения множества.
Пример 4. ПустьМ – множество граждан России. Зададим на этом множестве отношение r : два гражданина России находятся в отношении r , если они родились в одном месяце. Очевидно, что это отношение является отношением эквивалентности, заданным на множестве М. Каждый гражданин России порождает класс эквивалентности, которому принадлежат те граждане России, которые родились в одном месяце с ним. Понятно, что всего различных классов эквивалентности будет 12.
Разбиением непустого множества М называется такое семейство его непустых подмножеств, что каждый элемент множества М попадает точно в одно подмножество.
Справедлива следующая теорема.
Теорема 1. Пусть r –отношение эквивалентности, заданное на множестве М. Тогда фактор-множество М / r является разбиением множества М. 
Пример 5. Зададим на множестве целых чисел следующее отношение: будем говорить, что целые числа a и b сравнимы по модулю m ( m 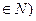 , если разность a – b делится на m, то есть
, если разность a – b делится на m, то есть  . В этом случае пишут: a
. В этом случае пишут: a 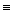 b (mod m).
b (mod m).
Легко показать, что отношение сравнения на множестве целых чисел является отношением эквивалентности. Это означает, что множество целых чисел разбивается на классы эквивалентности по этому отношению.
Классы эквивалентности по отношению сравнения называют классами вычетов по модулю m, фактор-множество по отношению сравнения называют множеством классов-вычетов по модулю m .
В классе вычетов, порожденном некоторым элементом a , находятся все целые числа, остаток при делении на m у которыхсовпадает с остатком при делении на m у числа a . Так как таких остатков m, то и классов вычетов тоже m . Удобнее всего порождать классы вычетов всевозможными остатками, которые могут получиться при делении на m .
Фактор-множество по отношению сравнения по модулю m обозначают символом Z  , Z
, Z  ={
={ 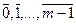 }.
}.
Пусть X , Y – произвольные непустые множества. Говорят, что задано отображение f множества X в множество Y, и пишут f: X ® Y, если каждому элементу х Î Х поставлен в соответствие однозначно определенный элемент y Î Y, обозначаемый f (х) (т.е. y = f ( x )). Отображение f : X ® Y иначе называется функцией на множестве X со значениями в множестве Y.
Отображение f : X ® X называется преобразованием множества X. Простейшее преобразование множества X – тождественное е: Х ® Х определяется так: ( " x Î X ) е(х) = х.
Пусть задано отображение f: X ® Y и x Î Х. Элемент y = f ( x ) называется образомэлемента х при отображении f, а элемент х – прообразомэлемента у. Если у – образ элемента х при отображении, то пишут х 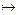 у. Если A Ì X, то полагают f ( A )= {f (х)| х Î А}. Множество f (А) называется образом множества А (при отображении f). Далее, если B Ì Y, то полагают f -1 (В)={х Î X | f ( x ) Î B} и множество f -1 (В) называется полным прообразом множества В (при отображении f).
у. Если A Ì X, то полагают f ( A )= {f (х)| х Î А}. Множество f (А) называется образом множества А (при отображении f). Далее, если B Ì Y, то полагают f -1 (В)={х Î X | f ( x ) Î B} и множество f -1 (В) называется полным прообразом множества В (при отображении f).
Отображение f : X ® Y называется инъективным, если для любых элементов х1, х2 множества X : х1 ¹ х2 Þ f (х1) ¹ f (х2).
Отображение f : X ® Y называется сюръективным или сюръекцией, если каждый элемент множества Y имеет хотя бы один прообраз, т. е. f -1 (у) ¹ Æ для любого y Î Y.
Отображение f называется биективным, если оно одновременно инъективно и сюръективно.
Два отображения f : X ® Y и j : U ® V называют равными и пишут f = j , если X = U , Y = V и f ( x ) = j ( x ) для каждого x Î X. Если Х={х1, х2, ..., х n}– конечное, Y –произвольное непустое множество, то отображение f : X ® Y принято записывать в виде  .
.
Пусть заданы два отображения f : X ® Y и g : Y ® Z. Поставив в соответствие каждому элементу х Î Х элемент g ( f ( x )) Î Z, получим отображение множества X в множество Z , которое называется произведением или композицией отображений f и g и обозначается g ◦ f .
Пусть f : X ® Y – биективное отображение. Тогда для любого элемента у Î Y существует единственный элемент х Î Х, такой что f ( x )= y. Отображение f -1 : Y ® X, при котором каждому у Î Y поставлен в соответствие его прообраз х Î Х, называется обратным отображению f .
Пусть Х={1, 2, ..., n}. Всякое упорядоченное расположение элементов множества X, т. е. расположение, в котором указано, какой элемент множества X является первым, какой – вторым и т. д., называется перестановкой множества X. Перестановку множества X , в которой a 1 является первым, а2 – вторым, ..., а n – последним элементом, будем обозначать (а1, а2, ..., а n ).
Говорят, что числа а i , а j образуют инверсию в перестановке (а1, а2, ..., а n ), если i < j , но а i >а j. Перестановка множества X называется четной, если число инверсий в ней четно, и нечетной – в противном случае.
Биективное преобразование множества называется иначе подстановкой этого множества. Пусть А – произвольное множество, содержащее не менее двух элементов, a , b – различные элементы множества А. Преобразование f множества А, при котором f ( a ) = b , f ( b ) = a , f ( x )= x ( " x Î X \{a , b}), называется транспозицией элементов a и b множества А и обозначается ( a , b ).
Всякую подстановку n-элементного множества (n ³2) можно разложить в произведение транспозиций, причем характер четности числа сомножителей во всех разложениях данной подстановки один и тот же. Подстановка конечного множества называется четной, если разлагается в произведение четного числа транспозиций, и нечетной – в противном случае.
Если а1, а2, ..., а k, k ³ 1, – различные элементы множества А, то преобразование f множества А, при котором f (а1)=а2, f (а2)=а3,…, f (а k -1) = а k , f (а k) = а1 , f ( x )=х, ( " x Î А\{а1, а2, ..., а k}, называется циклом длины k и обозначается (а1, а2, ..., а k). Очевидно, что (а1, а2, ..., а k) = (а2, а3,..., а k , а1) = ...=(а k , а1, ..., а k -1).
Всякий цикл длины единица является тождественной подстановкой множества А. Циклы длины два – это транспозиции множества А. Два цикла (а1, а2, ..., а k) и ( b 1 , b 2 , ..., bl ) называются независимыми, если а i ≠ bj , i =1,…, k ; j =1,…, l. Всякую нетождественную подстановку n-элементного множества можно разложить в произведение независимых циклов длины ³2, и это разложение однозначно с точностью до порядка записи сомножителей.
Задачи для самостоятельной работы
1. Пусть А – множество натуральных делителей числа 40. Перечислите элементы этого множества. Верно ли, что 6 Î A ; -8 Î A ; 4 Ï A ; 0 Ï A .
2. Записать символически:
а) множество всех общих кратных натуральных чисел a и b;
б) множество всех действительных чисел, квадрат которых меньше 2.
3. Записать следующие множества с помощью перечисления элементов, в виде числовых промежутков или с помощью символа Æ: 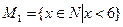 ;
; 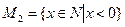 ;
; 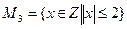 ;
;  ;
; 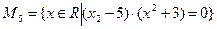 ;
; 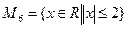 ;
; 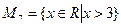 .
.
4. Каково множество решений каждого из уравнений (x 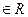 ):
):
а) х2 - 5x + 6 = 0; б) |х| = 2; в) |х| + x = 0.
Для каждого случая дайте геометрическую иллюстрацию.
5. Выяснить истинность следующих высказываний:
1) 2Î{1, 2, 3}; 2) {2}Î{1, 2, 3}; 3) {2}Î{{1}, {2}, {3}}; 4) 6Î{xÎNçx 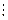 5}; 5) 6Î{xÎNç(36
5}; 5) 6Î{xÎNç(36 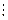 x)
x) 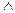 (x > 5)}.
(x > 5)}.
6. Установить вид отношения между множествами А и В (равенство, включение), если А – множество всех равносторонних треугольников; В – множество всех треугольников имеющих по два угла величиной в 60°.
7. Перечислить все подмножества множества {1; 2; 3}.
8. Обозначим через А множество всех квадратов, В – множество всех прямоугольников, С – множество всех параллелограммов, D – множество всех трапеций, Е – множество всех четырехугольников. Проверьте записи, установите, какие из них верны, какие ошибочны:
а) A Ì B Ì C Ì D Ì E; б) B Ì A Ì D Ì E.
9. Пусть А – множество всех точек плоскости, у которых ордината положительна, В – множество всех точек плоскости, у которых абсцисса положительна. Описать множества 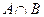 ,
, 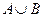 ,
,  ,
, 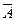 ,
,  ,
, 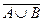 .
.
10. В каком случае AÈB=A, AÇB=B?
11. Показать, что если A Ì B, то AÇB = A.
12. Привести примеры числовых множеств A и B, таких, что:
а) A È B = R, A Ç B = Æ ; б) A È B = A, A Ç B = B.
13. Пусть A, B, C – подмножества множества K={1; 2; 3; 4; 5; 6}. Перечислить элементы множества B, если AÇA= Æ , BÇC= Æ , CÈ A={6}, BÈ C= K.
14. Постройте множества:
а) A = {(x, y) | x > 3} Ç B = {(x, y) | x £ 6};
б) A = {( x , y ) | x ³ 2}Ç B = {( x , y ) | y > 7};
в) {( x , y ) | x >0}Ç {( x , y ) | x £ 1}Ç {( x , y ) | y >-2}.
15. Найдите AÇB и AÈB, если:
а) A = {(x, y) | x2 + y2 - 4 £ 0}, B = {(x, y) | x × y = 0};
б) A = {(x, y) | 2 < x < 4}, B = {(x, y) | x + y £ 0};
в) A = {(x, y) | x - y = 0}, B = {(x, y) | 0 < y < 2}.
16. Дано множество A = {0, 1, 2, 3, 9}. Найдите разность A\B, если:
а) B = {1; 9}; б) B = Æ ; в) B = A.
17. Найдите AÇB, AÈB, A\B, B\A, если:
а) A = [4; 6], B = [2; 5]; б) A = [4; 6], B = [2; 5);
в) A = [4; 6], B = (2; 5]; г) A = [4; 6], B = (2, 5) .
18. Существует ли множество X, удовлетворяющее при любом A равенству: а) AÈX = A; б) AÇX = A.
19. Найдите дополнение:
а) множества натуральных чисел, оканчивающихся нулем до множества всех натуральных чисел, делящихся на 10;
б) множества решений уравнения 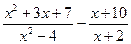 =0 до множества корней уравнения (5x - 13) × (x2 - 0,5x - 3) × x = 0.
=0 до множества корней уравнения (5x - 13) × (x2 - 0,5x - 3) × x = 0.
20. Постройте множества точек плоскости, координаты которых удовлетворяют следующим системам:
а) 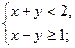 б)
б) 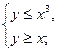 в)
в) 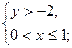 г)
г) 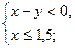 д)
д) 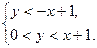
21. Докажите, что: а) AÈ(AÇB) = A; г) A \ B = AÇ 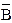 ;
;
б) AÇ(AÈB) = A; д) 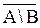 = AÈB;
= AÈB;
в) AÈ(B \ A) = A È B; е) (AÈB)Ç(BÈA) = A.
22. Упростить выражения:
а) AÇ( BÈÆ )Ç( AÈÆ )Ç( AÈВ); б) ( AÇ( BÈB ))È( AÇB );
в) 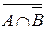 ÈB.
ÈB.
23. Каждое из следующих утверждений либо докажите, либо покажите при помощи диаграмм Эйлера, что оно не всегда верно:
а) (AÈB)ÇC = AÈ(BÇC); б) (A\B)ÈB = A; в) (AÇB) \ A = Æ .
24. Пусть множество A есть отрезок [1; 6], множество B – отрезок [2; 7], множество C – отрезок [-1; 3]. Найдите множества:
а) AÇCÇAÇA; б) (AÈB)ÇA; в) AÈ( ÆÇ(AÈB))È( ÆÇ(BÈC))ÈC.
25. В группе из 102 туристов 71 человек знают английский, 46 знают немецкий язык и 24 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни немецкого языка?
26. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги A, B и C. Результаты опроса оказались таковы: книгу A читало 24 учащихся, книгу B – 21, книгу C – также 21. Книгу A или B читали 32 ученика, A или С – 31, В или С – 30; все три книги прочли 9 учащихся. Сколько учащихся не читали ни одной из этих трех книг? Сколько учеников прочли только по одной книге?
27. Сколько элементов содержит множество A ´ B, если A имеет три элемента, а B – четыре элемента?
28. Перечислите элементы множеств A ´ B, B ´ A:
а) A = {1; 2}, B = {3; 4; 5}; б) A = {1}, B = {1; 2; 3}.
29. Составить прямое произведение множеств A={1; 2; 3}, B={4; 5; 6}. Доказать, что A ´ B ¹ B ´ A. Установить число элементов (A ´ B)Ç(B ´ A) .
30. Найдите прямые произведения A ´ B и B ´ A и дайте их графическое изображение: а) A = {x Î R |0 £ х £ 1}, B = {y Î R | 1 £ y £ 2}; б) A = {x Î R | x ³ 0}, B = {y Î R | y £ 0}.
31. На координатной плоскости построить следующие множества: а) (1; 2] ´ [1; 2); б) R ´ [-1; 1].
32. Доказать или опровергнуть, что
а) (A ´ B)È(C ´ D) = (AÈC) ´ (BÈD); б) А\(В 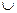 С)=(А\В)
С)=(А\В) 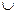 (А\С).
(А\С).
33. С помощью множества пар задайте отношения:
а) x < y на множестве A={1; 2; 3; 4};
б) x > y на множестве B={0,28; 0,3; 6};
в) x делится на y на множестве C = {1; 2; 3; 5; 6}.
34. На множестве B = {1; 2; 3; 4} задано отношение множеством пар {(1,1), (2, 2), (3, 3), (4, 4)}. Назовите это отношение.
35. Каким из свойств (симметричность, рефлективность, транзитивность) обладают отношения:
а) x – делитель y;
б) x взаимно просто с y;
в) x меньше y на множестве A = {2; 3; 4; -1/2; 6; -7}.
36. Для каждой строки таблицы придумать примеры отношений, обладающих свойствами, отмеченными знаком "+", и не обладающих свойствами, отмеченными знаком "-".
| Рефлексивность | Симметричность | Транзитивность |
| + + + + - - - - | + + - - + - + - | + - + - + + - - |
37. Являются ли следующие отношения на множестве R отношением эквивалентности: а) |x| = |y|; б) x×y ³0. Дайте геометрическую интерпретацию этого отношения.
38. Определить число инверсий в перестановке:
а) (5, 4, 1, 7, 6, 3, 2); б) (4, 3, 1, 8, 5, 2, 7, 6, 9); в) (n, n–1,…,2, 1).
39. Подберите i и k так, чтобы:
1) перестановка (1, 2, 7, 4, i , 5, 6, k , 9) была четной;
2) перестановка (1, i , 2, 5, k , 4, 8, 9, 7) была нечетной.
40. Доказать следующие свойства отношения делимости в кольце целых чисел:
а) любое целое число делится на само это число (а 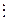 a );
a );
б) для любых целых чисел a , b , c верно: если а 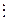 b и b
b и b 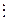 c, то а
c, то а 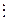 c;
c;
в) для любых целых чисел a , b , c верно: если а 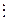 c и b
c и b 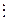 c, то a
c, то a 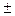 b
b 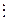 c;
c;
г) для любых целых чисел a , b , c верно: если а 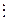 b, то а c
b, то а c 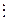 b;
b;
д) для любых целых чисел a , b верно: если а 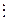 b и b
b и b 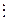 a , то a =
a , то a = 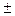 b .
b .
41. Доказать следующие свойства отношения сравнения по модулю m в кольце целых чисел:
а) любое целое число a сравнимо с самим этим числом по модулю m (a  a (mod m));
a (mod m));
б) для любых целых чисел a , b , d верно: если a  b (mod m) и b
b (mod m) и b  d (mod m), то a
d (mod m), то a  d (mod m);
d (mod m);
в) для любых целых чисел a , b , d , c верно: если a  b (mod m), d
b (mod m), d  c (mod m), то a
c (mod m), то a 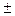 d сравнимо с b
d сравнимо с b 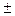 c по модулю m;
c по модулю m;
г) для любых целых чисел a , b , c верно: если a  b (mod m), то ac
b (mod m), то ac  bc (mod m);
bc (mod m);
д) для любых целых чисел a , b верно: если a  b (mod m), то и b
b (mod m), то и b  a (mod m);
a (mod m);
е) для любых целых чисел a , b , d , c верно: если a  b (mod m), d
b (mod m), d  c (mod m), то a d
c (mod m), то a d  b c(mod m).
b c(mod m).
ГЛАВА 2
АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
Алгебраические операции
Отношение, при котором каждой упорядоченной паре ( a , b ) элементов множества М ставится в соответствие единственный элемент с из этого же множества, называется бинарной алгебраической операцией, определенной на множестве М.
Бинарные алгебраические операции обозначают значком: *, ◦. Записывают: а ◦ b= c или a * b = c . Элемент с называют результатом бинарной алгебраической операции или композицией элементов a и b.
Кроме бинарных алгебраических операций существуют и нульместные (нульарные), унарные, тернарные,…, n -арные операции.
Нульместной алгебраической операцией на множестве М называется выделение (фиксация) какого-нибудь элемента множества.
Если каждому элементу из М соответствует другой (или тот же) элемент из М, то операция называется унарной. Унарную операцию называют также оператором.
Операция, при которой n элементам из множества М соответствует единственный элемент из М, называется n -арной или операцией ранга n.
Алгебраической системой (или алгебраической структурой) в универсальной алгебре называют множество с заданным на нём набором операций и отношений, удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений называется алгеброй, а система с пустым множеством операций — моделью.
В дальнейшем в пособии будут рассмотрены важнейшие алгебры: группы, кольца, поля, векторные пространства и показаны примеры их применения в различных задачах прикладного характера.
Обозначим множество всех заданных операций в А символом Ω (омега).
Тогда А называют основным множеством алгебры, а Î А – элементами алгебры А, Ω – главными операциями алгебры А. В случае конечного числа операций алгебру записывают: (А, ◦) или (М, ◦, *).
На множестве целых чисел сумма и разность любых двух целых чисел есть целое число, поэтому данные операции являются бинарными алгебраическими операциями на множестве целых чисел. Поэтому можно говорить об алгебре ( Z ,+,-). Также на множестве натуральных чисел операции сложения и умножения являются бинарными алгебраическими операциями, значит, можно рассмотреть алгебру ( N , +, ·).
Алгебраическую операцию можно задать посредством текстового описания закона, по которому из двух данных элементов получается третий.
Во-вторых, для небольших конечных множеств операцию можно задать с помощью таблиц Кэли, названных в честь выдающегося математика XIX века. Эти таблицы составляются следующим образом: заглавная строка таблицы заполняется в некотором порядке элементами множества, теми же элементами и в том же порядке заполняется заглавный столбец. Если на i-м месте в заглавном столбце стоит элемент a и на j-м месте в заглавной строке – элемент b, то на пересечении i-й строки и j-го столбца записывается символ, обозначающий произведение ab.
Алгебраическая операция ◦ на множестве М называется ассоциативной,если для любых трёх элементов a , b , c, принадлежащих множеству М, выполняется равенство: ( a ◦ b )◦ c = a ◦( b ◦ c ).
Алгебраическая операция ◦ на множестве М называется коммутативной, если ( " a , b Î M ) a ◦ b = b ◦ a .
Пусть задано множество М с двумя бинарными алгебраическими операциями *, ◦.
Бинарная операция * называется дистрибутивной относительно операции ◦, если ( " a , b , c Î G ) (а ◦ b) * c =( a * с) ◦ ( b * c ) (правая дистрибутивность) и с* (а ◦ b) =(с * а) ◦ (с * b ) (левая дистрибутивность).
Пример 1.
1. Операции сложения и умножения на множестве рациональных чисел Q являются коммутативными и ассоциативными.
2. Операция вычитания на множестве действительных чисел R не является коммутативной, ассоциативной.
3. На множестве целых положительных чисел зададим алгебраическую операцию по правилу: m ◦ n = mn. Данная операция не является коммутативной, т.к., например, при m =3, n =2 имеем 32 ≠23.
Элемент n Î М называется нейтральным элементом относительно бинарной алгебраической операции ◦, если длялюбого элемента a Î М выполняется равенствоa ◦ n = n ◦ a = a .
Необходимость двух равенств в определении продемонстрируем на следующем примере.
Пример 2.
На множестве действительных чисел без нуля рассмотрим операцию деления. Найдем нейтральный элемент.
Согласно определению нейтрального элемента ( " a Î R ) a :1= a – верно и 1: a =1/ a ¹ a, то есть элемент 1 не является нейтральным элементом. Это происходит из-за того, что операция деления на множестве R не является коммутативной. Именно из-за того, что операция может не оказаться коммутативной, в определении нейтрального элемента необходимы два равенства.
Поскольку существуют некоммутативные операции, то введём следующие определения:
Элемент n / называется левым нейтральным элементом операции ◦, если( " a Î M ) n / ◦ a = a .
Аналогично, n //ÎМ называется правымнейтральным элементом относительно операции ◦, если ( " a Î M ) a ◦ n // = a.
Теорема 1.1.
Если алгебра ( G , ◦) обладает нейтральным элементом n, то он единственный.
Доказательство (методом от противного).
Пусть n 1 и n 2 – два различных нейтральных элемента на множестве G относительно операции ◦. Тогда, так как n 1 – нейтральный элемент, то n 1 ◦ n 2 = n 2 (1), с другой стороны, n 2 – нейтральный элемент, поэтому результат операции n 1 ◦ n 2 = n 1 (2). Так как равны левые части равенств (1) и (2), то равны и правые части, а значит n 1 = n 2 , что противоречит допущению. Таким образом, наше предположение о существовании двух различных нейтральных элементов на множестве G неверно. Теорема доказана.
Теорема 1.2.
Если n / – левый нейтральный элемент, n // – правый нейтральный элемент алгебры ( G , ◦), то n / = n // .
Пример 3. Доказать, что во множестве К, содержащем не менее двух элементов, на котором формулой a ◦ b = b задана бинарная операция, не существует нейтрального элемента.
Доказательство (методом от противного).
Пусть в К существует нейтральный элемент n, и пусть а элемент из К, a 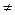 n . По определению нейтрального элемента a ◦ n = a, а по условию задания операции имеем: a◦n=n. Правые части подчеркнутых равенств равны, следовательно a = n. Полученное противоречие означает справедливость утверждения задачи.
n . По определению нейтрального элемента a ◦ n = a, а по условию задания операции имеем: a◦n=n. Правые части подчеркнутых равенств равны, следовательно a = n. Полученное противоречие означает справедливость утверждения задачи.
Элемент a / Î M называется симметричным элементу a Î M, если a ◦ a / = a / ◦ a = n .
Теорема 1.3.(о числе симметричных элементов у ассоциативной операции)
Если алгебраическая операция ◦ ассоциативна, то никакой элемент не может иметь более одного симметричного.
Доказательство (методом от противного).
Пусть для элемента a существует а1 и а2 – два различных симметричных элемента на множестве G относительно ассоциативной операции ◦. Тогда, по определению нейтрального элемента имеем: а1=а1◦е (1). Поскольку элемент а2, по нашему предположению является симметричным к а, то по определению симметричного элемента запишем: е= а◦а2 (2). Подставим равенство (2) в первое равенство, применим свойство ассоциативности, получим: а1=а1◦е =а1◦(а◦а2)=(а1◦а)◦а2=е◦а2=а2. Таким образом получили: а1=а2, что противоречит допущению. Таким образом, наше предположение о существовании двух различных симметричных элементов на множестве G неверно. Теорема доказана.
Для алгебраических операций часто используют аддитивную и мультипликативную формы записи.
| Аддитивная | Мультипликативная |
| Операцию называют : | |
| сложением | Умножением |
| Операцию обозначают и называют результат операции: | |
| a + b – сумма | a · b – произведение |
| нейтральный элемент обозначают и называют: | |
| 0 – нулем | 1 – единицей |
| симметричный элемент обозначают и называют: | |
| (-а) – противоположным | (а-1) – обратным для а |
| свойства коммутативности и ассоциативности записывают: | |
| a + b = b + а a + (b + c) = (a + b) + c | а · b = b · а a · (b · c) = (a · b) · c |
| свойства дистрибутивности записывают : | |
| ( a + b ) · c = a · с + b · c – правая, с · ( a + b ) = с · a +с · b – левая | |
Операция ◦ называется обратимой на множестве А, если для любых a , b Î A каждое из уравнений а ◦ х = b и х ◦ а = b имеет одно и только одно решение, принадлежащее А.
Теорема 1.4. (о связи между обратимостью операции и существованием единичного и обратного элементов).
Ассоциативная операция на множестве А обратима тогда и только тогда, когда в А существует единичный элемент и для ( " a Î A )( $ a -1 Î А).
Дата добавления: 2019-02-12; просмотров: 378; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!