Задачи для самостоятельной работы

1.Является ли множество Z полугруппой относительно операции:

а) сложения; б) вычитания?

2.Является ли множество N c операцией а ◦ b = а полугруппой?

3.Является ли множество R полугруппой относительно действия, выполняемого по правилу: а ◦ b = а² + b ²?

4.На множестве М², где М – некоторое множество, в котором бинарная операция ◦ определена по правилу (х, у) ◦ (z, t) = (х, t). Является ли М² полугруппой относительно этой операции?

5.Является ли множество М={2 ⁿ , n 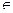N } с операцией умножения группой?

6.Является ли группой множество чисел вида а+ b 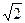относительно сложения, если а и b – любые рациональные числа?

7.Образуют ли группу четные числа относительно сложения?

8.Является ли множество М = {-1. 0, 1} группой относительно умножения?

9.Является ли множество квадратных трехчленов вида А = {ах² + b х + с | а, b , с Î R} группой относительно сложения?

10. Является ли множество (Z, ◦) – группой, если а ◦ b = 2а +3b?

11. Выяснить, образуют ли группу целые числа, кратные данному натуральному числу n относительно сложения.

12. Является ли множество М целых чисел, кратных трем, подгруппой аддитивной группы Z?

13. Доказать, что в аддитивной группе R ² множество пар вида (а,0) образует подгруппу.

14. Доказать, что множество четных чисел является подгруппой аддитивной группы Z целых чисел. Является ли множество нечетных чисел подгруппой группы Z?

15. Доказать свойства правых смежных классов.

16. Доказать, что любая подгруппа циклической группы сама является циклической.

17. В циклической группе порядка s найти порядки всех элементов, если a) s = 5; б) s = 8; в) s = 16.

18. Пусть G – циклическая группа, порожденная элементом g порядка 16. Найти подгруппу этой группы, порожденную элементом g .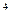

19. Пусть G – циклическая группа, порожденная элементом g порядка 12. Найти в G количество элементов порядка 4.

20. Пусть G – циклическая группа, порожденная элементом g порядка 10. Найти все правые смежные классы группы G по подгруппе H, порожденной элементом: a) g 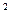; б) g 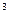; в) g .

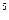Гомоморфизм и изоморфизм групп

Одним из важных понятий в теории групп является понятие гомоморфизма.

Пусть имеется две группы ( G ₁ ,◦) и ( G ₂ , * ).

Отображение f : G ₁ ® G ₂ называется гомоморфизмом групп, если:

( " g ₁ , g ₂ Î G ₁ ) f ( g ₁ ◦ g ₂ )= f ( g ₁ ) * f ( g ₂ ).

Множество G ₂ с заданной на нем операцией * называется гомоморфным образом группы G ₁ .

Слово «гомоморфный» в переводе с латинского означает «подобный по форме».

Примеры гомоморфизмов групп: f : ( Z ,+) → (2 Z ,+), f ( x ) = 2 x ,

f : ( R ,·) → ( R ,+), f ( x ) = lg x .

Теорема 4.1. (о гомоморфном образе группы).

Гомоморфный образ группы также является группой относительно своей операции.

Свойства гомоморфизмов групп

1.При гомоморфизме единица группы G ₁ отображается в единицу группы G ₂ .

2.( " g Î G₁) f(g 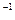) = ( f(g) ) .

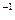Биективный гомоморфизм f : G ₁ ® G ₂ называется изоморфизмомгрупп ( G ₁ ,◦) и ( G ₂ , * ).

Термин «изоморфный» означает в переводе с латинского «одинаковый по форме».

Мономорфизм – гомоморфизм, являющийся одновременно инъективным отображением.

Эпиморфизм – гомоморфизм, являющийся одновременно сюръективным отображением.

Теорема 4.2.

Если группы G ₁ и G ₂ изоморфны, то любое свойство группы G ₁ переносится на группу G ₂ и обратно.

Ядром гомоморфизма групп называют множество элементов группы G ₁, чей образ совпадает с нейтральным элементом группы G ₂_.

Обозначение: Ker f = {g₁ Î G₁ / f(g₁)=e₂}=f ^-1(e₂).

Образом гомоморфизма f называют множество элементов из G_2,имеющих прообразы в G_1.

Обозначение: Im f = f (G₁)={g₂ Î G₂ /( $ g₁ Î G₁) g₂=f(g₁)}.

Основные свойства гомоморфизма групп:

1.Пусть f : G ₁ ® G ₂ – гомоморфизм групп. Тогда

а) При гомоморфизме единица группы G ₁ отображается в единицу группы G ₂ ;

б)( " g Î G ₁ ) f ( g 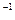)=( f ( g )) ;

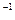в) Ker f – подгруппа группы G₁;

г) Im f – подгруппа группы G₂;

д) f – мономорфизм тогда и только тогда, когда Ker f = {е₁};

е) f – эпиморфизм тогда и только тогда, когда Im f = G₂ ;

ж) если f – изоморфизм, то f ^-1: G ₂ ® G ₁ также является изоморфизмом.

2.Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).

3. Теорема о гомоморфизмах групп.

Пусть имеется гомоморфизм f : G ₁ ® G ₂ . Фактор-группа по ядру этого гомоморфизма изоморфна образу f, т.е. G ₁ / Ker f @ Im f.

Изоморфизм группы на саму группу называется автоморфизмом группы.

Примеры гомоморфизмов групп:

· Пусть G – произвольная группа, а Î G – фиксированный элемент. Зададим отображение группы G в себя формулой x ® axa ^-1для любого х Î G . Заданное отображение – автоморфизм группы G, называемый внутренним.

· Отображение j : ( R ,+) ® ( R ⁺ , × ), заданное формулой j ( x )= a 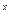, где а – фиксированный элемент из множества R \{1}, является изоморфизмом между аддитивной и мультипликативной группами, причем обратным к нему служит изоморфизм j ^-1 : ( R ⁺ , × ) ® ( R , +), j ^-1 (х)= log 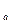x .

Дата добавления: 2019-02-12; просмотров: 274; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!