Задачи для самостоятельной работы

1. Выяснить, является ли множество чисел вида а + b 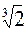, а, b Î Q с операциями сложения и умножения кольцом?

2. На множестве R действительных чисел с обычной операцией сложения, определим операцию умножения условием: а Ä b = b . Показать, что множество R не будет кольцом относительно данных операций.

3. Можно ли некоторое кольцо с единицей гомоморфно отобразить на некоторое кольцо без единицы?

4. Является ли подкольцом кольца Z относительно обычных операций множество четных чисел?

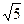5. Покажите, что множество чисел вида а + в +с + d 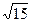, где а, в, с, d 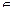Z является числовым кольцом, т.е. кольцом относительно обычных операций сложения и умножения над числами.

6. Докажите, что множество Z[ 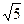] чисел вида а + b 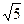, где а и b – любые целые числа, является числовым кольцом. Разрешимы ли в этом кольце уравнения (1 + 2 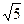)· х = -8+3 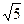, (-8 + 3 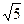)· х =1+2 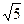, (3 + 2 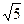) · х = 2 - 3 ?

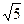7. Докажите, что множество А чисел вида 2а + 2 b , где а, b – любые целые числа, является числовым кольцом.

8. Справедливы ли формулы сокращенного умножения для элементов некоммутативных колец?

9. Выясните, является ли система (Z,Å,·) кольцом относительно обычного умножения и операции Å, выполняемой по правилу:

а Å b = а + b, если а – четное число, b– любое целое число,

а – b , если а – нечетное число, b – любое целое число

10. Является ли множество М матриц вида 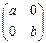, где а, b Î R коммутативным кольцом относительно матричного сложения и умножения? Имеются ли в данном множестве делители нуля? Если да, то какие?

11. Образует ли кольцо множество М двумерных векторов (х, у) с действительными координатами относительно следующих операций Å и Ä :(х₁, у₁) Å (х₂, у₂) = (х₁ + х₂, у₁ + у₂), (х₁, у₁) Ä (х₂, у₂) = (х₁ · х₂, у₁ · у₂).

12. Выясните, является ли множество Z кольцом относительно операции Ä и Å, определяемые равенствами: а Å b = а + b + 1,

а Ä b = а + b + а· b .

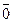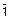13. Обозначим через Z ₂ множество, состоящее из двух элементов и . Операции сложения и умножения в этом множестве определим так: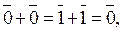

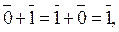
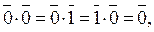
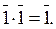
Является ли данное множество с заданными на нем операциями сложения и умножения кольцом?

14. Является ли множество целых чисел, кратных m , с обычным сложением и умножением кольцом?

15. Доказать, что (Z, +, Ä) является кольцом, если а Ä b =-а· b .

16.Составить таблицу сложения и умножения в кольце классов вычетов по модулю m, найти обратимые элементы и делители нуля, если: а) m=4; б) m=5; в) m=6.

Поле. Подполе. Основные свойства и примеры полей

Коммутативное кольцо с единицей (P, +, ∙), содержащее более одного элемента, называется полем, если любой ненулевой элемент этого кольца имеет обратный.

Примеры полей:

1. Множество рациональных чисел с операциями сложения и умножения рациональных чисел.

2. Множество действительных чисел с операциями сложения и умножения действительных чисел.

3. Множество P ={0, 1}, состоящее из двух чисел, где 0 – нулевой элемент, 1 – единичный является полем относительно операций сложения и умножения.

Простейшие свойства поля:

I. Так как поле является кольцом, то для него справедливы все свойства кольца.

II. Свойства, специфические для полей:

а) в поле не существует делителей нуля;

б) в поле можно ввести операцию деления: ;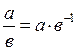

в) –а = (-1) · а;

г) ;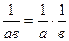

д) ;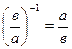

е) ;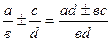

ж) критерий равенства дробей: ;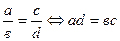

з) ;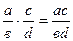

и) ас = вс 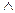с ≠ 0 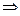а = в;

к) ав = 1 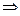а ≠ 0 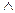в = а^-1;

л) ав 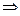= 0 а = 0 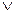в = 0;

м) .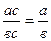

Непустое подмножество поля называется подполем этого поля, если оно само является полем относительно операций, заданных в поле.

Критерий подполя:

непустое подмножествоS поля Р является подполем поля Р тогда и только тогда, когда:

1) ( " а, b Î S ) а + b Î S ;

2) ( " а, b Î S ) а · b Î S ;

3) ( " а Î S ) -а Î S ;

4) ( " а Î S\{0} ) а^-1 Î S .

Пусть (Р₁, +, ∙ ), (Р₂, +, ∙ ) – два поля.

Понятия гомоморфизма и изоморфизма полей даются так же, как и соответствующие понятия для колец.

Рассмотрим подробно очень важное поле – поле комплексных чисел.

Термин «комплексное число» ввел в 1803 году Л. Карно, но в употребление он вошел только благодаря работам К. Гаусса в 1831 году. На рубеже XVII-XVIII веков была построена общая теория корней n-й степени сначала из отрицательных, а потом из любых комплексных чисел, а полное геометрическое истолкование «мнимым» величинам дали в своих работах К. Вессель и Ж. Арган.

Как известно, уравнение х²+а=0 не имеет решений в поле действительных чисел при а>0. В частности, неразрешимо уравнение х²+ 1 = 0. Возникает вопрос: нельзя ли построить такое расширение поля R, в котором содержится хотя бы один элемент, удовлетворяющий данному уравнению.

Дата добавления: 2019-02-12; просмотров: 311; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!