Гомоморфизм и изоморфизм алгебр
Пусть имеются две алгебры: (А, Ω) и (А´, Ω´). Говорят, что задано отображение алгебры (А, Ω) на алгебру (А´, Ω´), если указано отображение множества А на множество А´ и если операциям на А взаимно однозначно сопоставлены операции на А´.
Отображение множества А на множество А´ будем обозначать буквами f , φ; при этом элемент а´ является образом элемента а, обозначается а´= φ (а).
Отображение φ сохраняет операции, если для любых соответствующих друг другу операций – операции ◦ на А и операции * на А´ выполняется условие: φ (а1 ◦ а2) = φ (а1) * φ (а2) (рис.4).
Отображение алгебры (А, Ω) на алгебру (А´, Ω´), сохраняющее операции, называют гомоморфизмом.
Биективный гомоморфизм алгебры (А, Ω) на алгебру (А´, Ω´), называют изоморфизмом.
Если существует изоморфизм алгебры (А, Ω) на алгебру (А´, Ω´), то алгебры называют изоморфными и пишут A  А.
А.

Рис.4. Гомоморфизм алгебр
Задачи для самостоятельной работы
1. Является ли данное отображение гомоморфизмом, изоморфизмом указанных алгебр?
а) ƒ: (Z, +) → (Z, +), ƒ(а) = а + 1;
б) ƒ: (Q [  ], +) → (Q[
], +) → (Q[  ], +), ƒ(а +b
], +), ƒ(а +b  ) = а + b
) = а + b  ;
;
в) ƒ: (Z, +) → (Z, +), ƒ(а) = 2а;
г) ƒ: ( R + , ∙) → ( R , +), ƒ(а) = ln а;
д) φ: ( N , +) → ( R , ·), φ( n ) =  ;
;
е) φ: ( Q , +, ·) → ( R , +, ·), φ(  )=2х + 3у +
)=2х + 3у +  .
.
Группы, основные свойства групп
Среди различных алгебр важнейшую роль в математике и ее приложениях играют группы. Теория групп используется при изучении геометрических преобразований, в теории алгебраических уравнений, в топологии, атомной физике, криптографии и т.д.
Истоки теории групп лежат в нескольких разделах математики:
а) теории решения алгебраических уравнений в радикалах (Абель, Галуа, Лагранж);
б) геометрии (Кэли, Клейн и др.);
в) теории чисел (Гаусс, Эйлер).
Группой G называется алгебра с одной бинарной алгебраической операцией *, обладающей следующими свойствами:
1) ( " a, b, c Î G) a * (b * c)=(a * b) * c;
2) ( $ n Î G)( " a Î G) a * n=n * a=a;
3) ( " a Î G)( $ a/ Î G) a/ * a=a * a/=n.
Операция *, удовлетворяющая свойствам 1)-3), иногда называется групповой операцией, а элементы множества G – элементами группы.
Группы бывают конечные и бесконечные. Число элементов конечной группы G называется ее порядком и обозначается ½G½.
Свойством коммутативности группа может не обладать. Если же в группе выполняется свойство коммутативности для любых элементов, то она называется коммутативной или абелевой (в честь норвежского математика Н. Абеля (1802-1829)).
Введем следующие определения:
· множество с алгебраической операцией называют группоидом;
· группоид с ассоциативной операцией называют полугруппой;
· полугруппу с нейтральным элементом называют моноидом.
Связь между данными алгебраическими структурами прекрасно иллюстрирует рисунок, из которого видно, что любая группа является полугруппой, а любая полугруппа является группоидом.

Рис.5. Связь между алгебраическими структурами
Приведем примеры групп:
| Группа | Операция | Нейтр. Элемент | Симметричный | |
| а | a/ | |||
| Z | + | 0 | а | -a |
| Q | + | 0 | p/q | -(p/q) |
| 2Z | + | 0 | a=2a1 | -2a1 |
{а + b  , а, в , а, в  Z} Z}
| + | 0 |  a+b a+b
|  -a+(-b) -a+(-b)
|
| Q+ | · | 1 | p | 1/p |
| {-1; 1} | · | 1 | -1 1 | -1 1 |
| {2m, m Î Z} | · | 20=1 | 2 m | 2- m |
Простейшие свойства групп (на мультипликативном языке):
1) В каждой группе существует только одна единица (по теореме о единственности нейтрального элемента).
2) В каждой группе любой элемент g имеет единственный ему обратный элемент g -1 Î G .
3) Во всякой группе каждое из уравнений ax = b и ya = b при любых a , b Î G имеет решение и притом только одно.
Доказательство. Элемент a -1 b есть решение уравнения ax = b , так как a ( a -1 b )=(а a -1 ) b =е b = b . С другой стороны, если с – произвольное решение уравнения ax = b , то с=ес=( a -1 а)с= a -1 (ас)= a -1 b . Таким образом, если существует решение этого уравнения, то оно единственное и равно элементу a -1 b . Аналогично доказывается, что элемент ba -1 является решением уравнения ya = b .
4) Справедливы законы сокращения:
("a , b , с Î G ) ab = cb Þ a = c (сокращение справа),
("a , b , с Î G ) ba = bc Þ a = c (сокращение слева).
5) ("a, b Î G) ab=a Þ b=1 и ("a, b Î G) ba=a Þ b=1.
6) ("a , b Î G ) ab =1 Þ a -1 = b Ù b -1 = a .
7) В группе имеет место обобщенный закон ассоциативности, а если группа абелева – обобщенный закон коммутативности.
8) ("a Î G) (a-1) -1=a.
9) ("a1, a2,… an Î G) (a1 a2… an) -1= (an) -1(an-1) –1…(a1) –1.
Если a 1 = a 2 = a 3 =…= an = a, то произведение a·a·a·…·a обозначают символом an и называют n-ой степенью элемента а.
Степень элемента обладает свойствами, похожими на свойства степеней для натуральных чисел:
("a, b Î G) ("n, m Î Z) am·an= am+n; (am)n= amn.
Если группа коммутативна, то ( ab ) n = an · bn .
Если рассматривается группа с операцией сложения, то говорят о кратных элемента a и пишут: a + a + a +…+a = na; при этом выполняются соотношения: ma + na =( m + n ) a ; n ( ma )=( nm ) a .
Непустое подмножество H группы ( G ,◦) называется подгруппой группы G, если оно само является группой относительно той же операции, что и группа G . В этом случае пишут: H  G .
G .
Критерий подгруппы:
Непустое подмножество H группы G является подгруппой группы G тогда и только тогда, когда:
1) ( " a,b Î H) a × b Î H; 2) ( " a Î H) (a-1) Î H.
Примеры подгрупп:
1. Тривиальные (несобственные) подгруппы. Каждая группа имеет единичную подгруппу и сама является своей подгруппой.
2. Легко показать, что подмножество Н = {2k | k Î Z)} аддитивной группы Z является подгруппой этой группы.
3. Теорема 3.1. Пересечение подгрупп группы также является подгруппой этой группы.
Пусть G – мультипликативная группа, Н – подгруппа группы G , g – элемент группы G .
Множество  называется правым смежным классом группы G по подгруппе Н, порожденным элементом g .
называется правым смежным классом группы G по подгруппе Н, порожденным элементом g .
Отметим свойства правых смежных классов.
1) Каждый правый смежный класс не пуст.
2) Любой элемент подгруппы Н порождает класс, совпадающий с подгруппой Н.
3) Если элемент g  принадлежит какому-то правому смежному классу, то он порождает этот класс.
принадлежит какому-то правому смежному классу, то он порождает этот класс.
4) Любые два смежных касса либо не пересекаются, либо совпадают.
5) Объединение всех смежных классов совпадает с группой G .
Из свойств правых смежных классов следует, что множество правых смежных классов задает разбиение группы G . Поэтомуна множестве G можно задать следующее отношение, являющееся отношением эквивалентности: элементы a и b группы G находятся вэтом отношении, если они принадлежат одному правому смежному классу.
Аналогично определению правого смежного класса можно дать определение левого смежного класса gH. Также можно рассматривать на мультипликативную, а аддитивную группу G . В этом случае правый смежный класс записывают следующим образом: H + g.
В теории групп очень важна следующая теорема, связывающая порядок конечной группы и порядок любой ее подгруппы.
Теорема 3.2. (Теорема Лагранжа). Пусть G – группа, Н –подгруппа группы G , | G |= n , | H |= k. Тогда  .
.
Доказательство. Выпишем все элементы подгруппы Н:
Н ={  }.
}.
Заметим, что подгруппу Н можно считать правым смежным классом, порожденным нейтральным элементом группы G.
Если не все элементы группы G перечислены, то возьмем один из оставшихся (например, элемент  ) и рассмотрим правый смежный класс группы G по подгруппе Н, порожденной элементом g
) и рассмотрим правый смежный класс группы G по подгруппе Н, порожденной элементом g  :
:
Н g  ={
={  }.
}.
Если в группе G имеется элемент  , не вошедший ни в одно из множеств Н, Н g
, не вошедший ни в одно из множеств Н, Н g  , то рассмотрим правый смежный класс группы G по подгруппе Н, порожденной элементом g
, то рассмотрим правый смежный класс группы G по подгруппе Н, порожденной элементом g  :
:
Н g  = {
= {  }.
}.
Так продолжим до тех пор, пока не будут исчерпаны все элементы группы G. Пусть последним смежным классом будет класс, порожденный элементом g  :
:
Н g  = {
= {  }.
}.
Из того, как получены строки, ясно, что каждый элемент группы G входит в некоторый смежный класс.
В любом смежном классе элементы попарно различны. В Н, очевидно, все элементы различны. Возьмем правый смежный класс Н g  . Положим, что в ней
. Положим, что в ней  ( i
( i  . Умножив это равенство справа на
. Умножив это равенство справа на  , получим, что в классе Н есть совпавшие элементы, что невозможно. Аналогично, попарно различны элементы каждого из остальных классов.
, получим, что в классе Н есть совпавшие элементы, что невозможно. Аналогично, попарно различны элементы каждого из остальных классов.
Может ли быть так, что совпадают элементы разных классов? Пусть, к примеру, классы Н g  и Н g
и Н g  имеют один и тот же элемент
имеют один и тот же элемент  . Но в этом случае
. Но в этом случае  должен являться элементом класса Н g
должен являться элементом класса Н g  , что противоречит выбору элемента
, что противоречит выбору элемента  .
.
Таким образом, в смежные классах Н, Н g  ,…, Н g
,…, Н g  попаливсеэлементы группы G и каждый элемент встречается один раз. Тогда из равенства n = ks следует, что
попаливсеэлементы группы G и каждый элемент встречается один раз. Тогда из равенства n = ks следует, что  .
.
Из теоремы Лагранжа следует, что в группе простого порядка нет смысла искать подгруппы, отличные от единичной и самой группы.
Пусть G – группа и g  G. Возьмем множество Н =
G. Возьмем множество Н =  . Пользуясь критерием, нетрудно убедиться в том, что Н
. Пользуясь критерием, нетрудно убедиться в том, что Н  G . Н назовём циклической подгруппой, порожденной элементом g .
G . Н назовём циклической подгруппой, порожденной элементом g .
Введем обозначения Н=  . Элемент g будем называть образующим (порождающим) группу Н.
. Элемент g будем называть образующим (порождающим) группу Н.
Если Н= G, то группа G оказывается циклической, порожденной элементом g.
Итак, в группе G взята циклическая подгруппа Н=  , порожденная элементом g. Следующие условия равносильны:
, порожденная элементом g. Следующие условия равносильны:
1) степени  , попарно различны;
, попарно различны;
2) для целых чисел п и k равенство  выполняется тогда и только тогда, когда n = k;
выполняется тогда и только тогда, когда n = k;
3) для любого целого п равенство  выполняется только в том случае, если n = 0 ;
выполняется только в том случае, если n = 0 ;
4)  для любого натурального числа п;
для любого натурального числа п;
5) H  Z.
Z.
Будем говорить, что порядок элемента бесконечен (писать: ord g =  ), если для элемента g выполняется одно из пяти условий.
), если для элемента g выполняется одно из пяти условий.
Что будет происходить, если перечисленные выше условия не выполняются? В этом случае для элемента g найдутся целые числа n и k такие, что  и
и  . Положив, что k < n, получим
. Положив, что k < n, получим 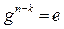 для n –
для n –  N. Поскольку множество натуральных чисел вполне упорядочено, для нашего элемента g найдется наименьшее натуральное число s, такое, что
N. Поскольку множество натуральных чисел вполне упорядочено, для нашего элемента g найдется наименьшее натуральное число s, такое, что  . Это число назовем порядком элемента g .
. Это число назовем порядком элемента g .
Запись ord g = s будет означать, что s  N,
N,  и если t
и если t  N таково, что
N таково, что 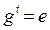 , то s
, то s  t .
t .
Легко увидеть, что ord g = s в том и только том случае, если | H |= s, где Н=  .
.
Показано, что любой элемент конечной группы порождает циклическую подгруппу этой группы, порядок которой совпадает с порядком этого элемента. С учетом этого получаем следующее следствие из теоремы Лагранжа.
Следствие 1. Порядок конечной группы делится на порядок любого ее элемента.
Следствие 2. Если |G|=n, то  для любого элемента g
для любого элемента g  G.
G.
Теорема 3.3. Пусть (G,  ) – группа, g
) – группа, g  G, ord g = s , s
G, ord g = s , s  N.
N.
Справедливы следующие утверждения:
1) (  n
n  Z) (
Z) ( 

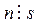 );
);
2) (  n , k
n , k  Z) (
Z) ( 

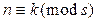 );
);
3) (  k
k  Z) (ord
Z) (ord  =
=  ) (здесь символом ( k , s ) обозначен положительный наибольший общий делитель чисел k и s).
) (здесь символом ( k , s ) обозначен положительный наибольший общий делитель чисел k и s).
Доказательство.
1) Очевидно, если 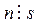 , то
, то  .
.
Пусть целое число п таково, что  . По теореме о делении с остатком в кольце целых чисел, имеем n = sq + r , 0
. По теореме о делении с остатком в кольце целых чисел, имеем n = sq + r , 0  r < s . С учетом этого
r < s . С учетом этого  . Если 0< r < s , то получаем противоречие с условием ord g = s ; поэтому r = 0, и значит,
. Если 0< r < s , то получаем противоречие с условием ord g = s ; поэтому r = 0, и значит, 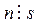 .
.
2) Это утверждение легко доказывается использованием утверждения (1).
3) Введем обозначения: ( k , s )= d . Будем иметь  ,
,  , где
, где  и
и  – взаимно простые целые числа. В новых обозначениях следует доказать, что ord
– взаимно простые целые числа. В новых обозначениях следует доказать, что ord  =
=  . Ясно, что
. Ясно, что 
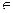 N . Далее,
N . Далее,  . Пусть теперь t
. Пусть теперь t  N и
N и  . Будем иметь:
. Будем иметь:






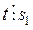

 .
.
По определению порядка элемента, ord  =
=  .
.
Теорема 3.4. Конечная группа порядка п является циклической в том и только в том случае, если в ней найдется элемент порядка п.
Дата добавления: 2019-02-12; просмотров: 564; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
