Задачи для самостоятельной работы
1. Какому полю изоморфно простое поле характеристики ноль? Какое условие выполняется в поле характеристики 0?
2. Какому полю изоморфно простое поле характеристики р? Какое условие выполняется в поле характеристики p?
3. Пусть Fq – конечное поле характеристики р. Как связаны числа q и p?
4. Докажите, что характеристика конечного поля является простым числом.
5. Найдите примитивный элемент поля F11. Постройте таблицу индексов этого поля. Найдите все примитивные элементы поля F11.
6. Дайте определение минимального многочлена алгебраического элемента aÎР. Докажите свойства минимального многочлена.
7. Докажите, что порядок любого элемента мультипликативной группы конечного поля взаимно прост с характеристикой этого поля.
8. Является ли полем фактор-кольцо F2[x]/<x5+x+1>?
9. Постройте таблицу индексов поля F8, используя неприводимый над F2 многочлен f(x) = x3+x2+1.
ГЛАВА 3
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Системы линейных уравнений часто возникают при решении многих математических задач. Существуют различные методы их решения. При этом неважно, из какого именно множества берутся коэффициенты и свободные члены систем линейных уравнений, главное, что они принадлежат некоторому полю P. Это означает, что можно пользоваться всеми аксиомами и свойствами полей: так, к примеру, точно известно, что любой ненулевой элемент из поля имеет обратный, что очень важно при применении элементарных преобразований в системе линейных уравнений.
При решении систем линейных уравнений удобно пользоваться матрицами, любую систему линейных уравнений можно задать в матричном виде. Матрицы с введенными операциями образуют векторное пространство (если рассматривать сложение матриц и умножение матриц на скаляр), множество квадратных матриц относительно операций сложения и умножения является кольцом с единицей. В этом кольце некоторые матрицы имеют обратные, множество таких матриц с операцией умножения является группой. Если матрица коэффициентов системы линейных уравнений является обратимой, то система имеет единственное решение. Критерий совместности системы линейных уравнений также формулируется с помощью понятий теории матриц. Именно поэтому глава начинается с изучения матриц.
Матрицы
Матрицей размерности m на n (m  n ) над полем P называется прямоугольная таблица элементов поля P , имеющая m строк и n столбцов, при этом пишут: A =
n ) над полем P называется прямоугольная таблица элементов поля P , имеющая m строк и n столбцов, при этом пишут: A = 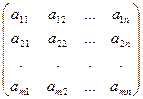 .
.
Множество таких матриц обозначают M 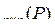 .
.
Элемент a  матрицы A расположен в i-той строке и в j-том столбце матрицы A. Любые строки и столбцы матрицы, в свою очередь, являются матрицами.
матрицы A расположен в i-той строке и в j-том столбце матрицы A. Любые строки и столбцы матрицы, в свою очередь, являются матрицами.
Две матрицы A и B одинакового размера называются равными, если они совпадают поэлементно.
Пусть A 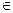 M
M 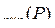 , B
, B 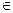 M
M 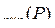 , то есть матрицы A и B имеют одинаковую размерность. Кратко их будем записывать так:
, то есть матрицы A и B имеют одинаковую размерность. Кратко их будем записывать так: 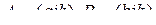 , где
, где 
Суммой матрицA и B называется матрица C 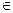 M
M 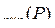 , элементы которой находятся по следующему правилу:
, элементы которой находятся по следующему правилу: 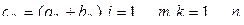 Теорема 1.1. Алгебра M
Теорема 1.1. Алгебра M 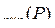 с операцией сложения является абелевой группой.
с операцией сложения является абелевой группой.
Произведением матрицы A на скаляр k называется матрица 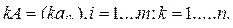
Произведение матриц на скаляр обладает свойствами:
1) 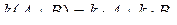
2) 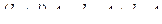 ,
,
3) 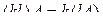 ,
,
4) 1 A = A,
для любых матриц A , B из множества M 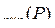 и элементов k , l поля P.
и элементов k , l поля P.
Из теоремы 1.1. и свойств произведения матриц на скаляр следует справедливость следующей теоремы.
Теорема 1.2. Множество матриц M  с операциями сложения матриц и умножения матриц на скаляр является векторным пространством над полем P.
с операциями сложения матриц и умножения матриц на скаляр является векторным пространством над полем P.
На множестве матриц также можно задать и операцию умножения матриц. При этом две матрицы можно умножить только в случае, если число столбцов первой матрицы равно числу строк второй.
Произведением матриц A размерности m  nиB размерности n
nиB размерности n  k называется матрица
k называется матрица 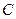 размерности m
размерности m  k, элементы которой находятся по формуле:
k, элементы которой находятся по формуле: 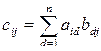 .
.
Говорят также: для того, чтобы найти элемент 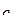 , нужно элементы i-ой строки матрицы A умножить на соответствующие элементы j-го столбца матрицы B и сложить полученные произведения.
, нужно элементы i-ой строки матрицы A умножить на соответствующие элементы j-го столбца матрицы B и сложить полученные произведения.
Свойства умножения матриц:
1) умножение матриц не коммутативно;
2) умножение матриц ассоциативно, то есть 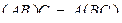 ;
;
3) умножение матриц дистрибутивно относительно сложения матриц, то есть 
Замечание. В свойствах 2) и 3), разумеется, матрицы 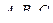 такой размерности, что все произведения существуют.
такой размерности, что все произведения существуют.
Пример 1. Вычислить произведения матриц:
а)  ; б)
; б) 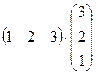 ; в)
; в) 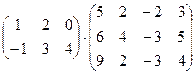 .
.
Решение:
а)  =
= 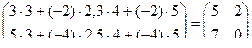 ;
;
б) 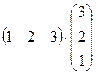 =(1
=(1  ;
;
в) 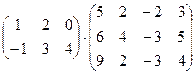 =
=  .
.
Можно рассмотреть множества матриц, в которых одновременно заданы операции сложения и умножения.
Квадратными называются матрицы, у которых число строк и столбцов одинаковое.
Если у квадратной матрицы n строк, то говорят, что матрица имеет размерность n . Множество таких матриц обозначают символом M  ( P ). В этом множестве важную роль играет единичная матрица.
( P ). В этом множестве важную роль играет единичная матрица.
Матрица Е = 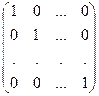 называется единичной матрицей.
называется единичной матрицей.
Заметим, что если A , E – матрицы одной размерности, то 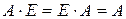 , то есть E является нейтральным элементом относительно операции умножения в алгебре квадратных матриц.
, то есть E является нейтральным элементом относительно операции умножения в алгебре квадратных матриц.
Теорема 1.3. Множество M  ( P ) с операциями сложения и умножения является кольцом c единицей.
( P ) с операциями сложения и умножения является кольцом c единицей.
Пример 2. Найти значение многочлена 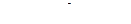 от матрицы
от матрицы 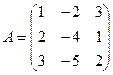 .
.
Решение. В запись многочлена 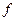 вместо переменной
вместо переменной 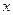 подставляем матрицу A и находим значение 3 A
подставляем матрицу A и находим значение 3 A  -2 A +5Е, где Е – единичная матрица 3-го порядка:
-2 A +5Е, где Е – единичная матрица 3-го порядка:
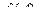
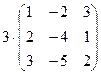
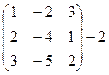
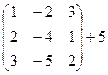
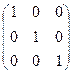 =
=
= 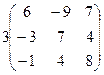
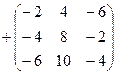

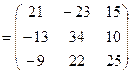 .
.
Возникает также вопрос: у любой ли квадратной A матрицы существует обратная ей матрица, то есть такая матрица A 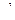 , что справедливо равенство:
, что справедливо равенство:  . Оказывается, нет. В параграфе 5 этой главы будет показано, какие матрицы имеют обратные, и как их находить.
. Оказывается, нет. В параграфе 5 этой главы будет показано, какие матрицы имеют обратные, и как их находить.
Дата добавления: 2019-02-12; просмотров: 196; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
