Задачи для самостоятельной работы
1. Выяснить, можно ли представить вектор c в виде линейной комбинации векторов a и b:
а) с=(1,2,3,4), a=(2,3,4,5), b=(3,4,5,6);
б) с=(2,2,-3,1), a=(2,3,5,1), b=(3,2,5,2);
в) с=(1,0,0,0), a=(2,-3,4,-5), b=(3,4,5,6);
г) с=(2,3,4), a=(3,4,5), b=(4,5,6).
2.Выяснить, является ли линейно зависимой система векторов:
а)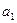 
=(1,1,2,1), 
= (-3,2,3,0), 
=(2,4,-2,3), =(4,1,2,1);
б) 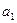=(5,3,2,1), = (4,2,1,0), =(3,1,0,1), =(2,0,-1,-2);
в) 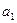=(2,1,2,1), = (4,2,4,0), =(1,4,-2,3), =(3,2,1,0);
г) 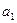=(6,4,2,0), = (3,2,1,2), =(1,4,-2,3), =(1,1,2,1).
3. Найти ранг и базис системы векторов:
а) 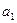=(4,3,2,1), = (3,2,1,0), =(2,1,0,-1), =(1,0,-1,-2);
б) 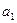=(2,1,2,1), = (4,2,4,1), =(1,4,-2,3), =(3,2,1,0);
в) 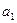=(1,1,2,1), = (-3,2,3,0), =(2,4,-2,3), =(4,1,2,1);
г) 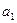=(1,2,3,4), = (3,4,5,6), =(5,6,7,8), =(7,8,9,10).
Все векторы системы выразить через базис.
Ранг матрицы
Рассмотримматрицу A размерности m на n над полем P:
A = 
.
Строки этой матрицы можно рассматривать как n-мерные векторы, столбцы – как m-мерные векторы. У этих систем векторов можно найти базис и ранг.
Строчечным рангом матрицы называется ранг системы векторов-строк этой матрицы; столбцовым рангом матрицы называется ранг системы векторов-столбцов этой матрицы.
Со строками (столбцами) матрицы A можно производить те же преобразования, что и в системе линейных уравнений.
Теорема 4.1. Строчечные (столбцовые) ранги матрицы A и матрицы, полученной из A с помощью элементарных преобразований над строками (столбцами) матрицы A, совпадают.
Для того, чтобы найти строчечный (столбцовой) ранг матрицы нужно матрицу путем элементарных преобразований над строками (столбцами) привести к ступенчатому виду. Ранг матрицы равен числу оставшихся строк (столбцов).
|
|
|
Пример 1. Найти строчечный и столбцовый ранги матрицы
A = 
.
Найдем сначала строчечный ранг матрицы:
A = ~ 
~ 
~ 
Значит, строчечный ранг матрицы равен двум.
Для нахождения столбцового ранга матрицы найдем строчечный ранг у транспонированной матрицы A 
–матрицы, полученной из матрицы A заменой строк на столбцы.
A ~ 
~ 
~ 
~ 
.
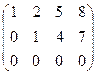Столбцовый ранг матрицы также равен двум.
То, что в примере строчечный и столбцовый ранги матрицы совпали, не случайно. Справедлива следующая теорема.
Теорема 4.2. Строчечный и столбцовый ранги матрицы равны.
Вследствие справедливости этой теоремы можно говорить о ранге матрицы, подразумевая под этим понятием один из рангов матрицы – строчечный или столбцовый.
С понятием ранга матрицы связан и критерий совместности системы линейных уравнений.
Теорема 4.3. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы коэффициентов системы равен рангу расширенной матрицы этой системы.
Задачи для самостоятельной работы
1. Найти ранг матрицы:
а) 
; б) 
; в) 
.
2. Найдя ранг матрицы коэффициентов системы и расширенной матрицы, выясните, совместна ли система линейных уравнений:
|
|
|
а) 
; б) 
;
в) 
; г) 
.
Обратимые матрицы
С помощью понятия ранга можно дать определение очень важного типа матриц.
Квадратная матрица 
размерности n называется невырожденной, если её ранг равен n, в противном случае она называется вырожденной.
Другими словами, матрица является невырожденной, если ее строки линейно независимы и вырожденной, если её строки линейно зависимы. При рассмотрении матриц в параграфе 1 этой главы возник вопрос: любая ли квадратная матрица A является обратимой, то есть существует ли такая матрица A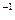 
, что справедливо равенство: 
. На этот вопрос отвечает следующая теорема.
Теорема 5.1. Квадратная матрица обратима тогда и только тогда, когда она является невырожденной.
Опишем алгоритм нахождения обратной матрицы для невырожденной матрицы. Приписываем к матрице справа единичную матрицу. Далее с помощью элементарных преобразований над строками полученной матрицы приводим матрицу к единичной матрице 
. Тогда на месте матрицы оказывается матрица A .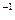
Пример 1. Найти 
, если 
.
Решение. Составим матрицу (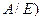 
: ( = 
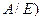и далее с помошью элементарных преобразований над строками полученной матрицы приводим к единичной матрице .
|
|
|
После первого шага получаем матрицу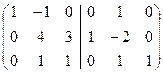 
(меняем местами первую и вторую строки, затем, как это делали в методе Гаусса, получаем нули в первом столбце во второй и третьей строке).
Второй шаг: с помощью второй строки получим нули во втором столбце (первую строку умножаем на 4 и прибавляем к ней вторую, третью строку умножим на (-4) и прибавляем к ней вторую):
.
Третий шаг: получаем нули в третьем столбце с помощью третьей строки (умножаем её на 3 и прибавляем ко второй и первой строке): 
.
В заключение первую и вторую строку умножаем на ¼, получаем :
.
Справа от единичной матрицы стоит обратная матрица :
.
Пример 2. Решить матричные уравнения:
а) 
; б) 
;
с) 
Решение.
а) Матрица А невырожденная, для неё существует обратная матрица , поэтому:
или 
.
Заметим, что умножить обе части уравнения AX = C на матрицу в данном примере нужно обязательно слева, так как умножение матриц некоммутативно.
Находим :
~ 
~ 
~ 
.
= 
= 
.
б) Матрица В вырожденная, обратная не существует. Попробуем решить уравнение методом неопределенных элементов. Пусть 
, тогда 
= 
, умножим матрицы в левой части равенства и приравняем элементы на одинаковых местах, получим систему равенств: 
Решив эту систему, получаем, что любая матрица вида 
является решением матричного уравнения.
|
|
|
В том случае, когда в системе линейных уравнений число уравнений совпадает с числом переменных и матрица коэффициентов невырожденная, систему можно решать с помощью нахождения обратной матрицы для матрицы коэффициентов.
Рассмотрим систему: 
.
Эту систему можно записать в матричном виде:
= 
или AX = B.
Если матрица коэффициентов А невырожденная, то для неё существует обратная матрица , поэтому X = A 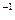B .
Пример 3. Решить систему линейных уравнений 
матричным методом. Сделать проверку.
Имеем: 
Тогда данная система запишется в виде матричного уравнения AX = B .
, 
.
Дата добавления: 2019-02-12; просмотров: 181; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!