Задачи для самостоятельной работы
1. Составить таблицу зашифрования для аффинного шифра с ключом a, b и зашифровать слово ключ:
а) a =3, b =7; б) a =5, b =10; в) a =11, b =7; г) a =17, b =7.
2. Расшифровать сообщение T, зашифрованное с помощью аффинного шифра (соответствие между буквами русского языка и элементами кольца классов-вычетов Z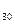 
такие же, как в примере 1) если:
а) T = дгштгцтгш, буква а при шифровании перешла в г, ф в в;
б) T = лгфеукикфдцлвфкюкк, буква а при шифровании перешла в д, ф в т;
в) T =жгунненукезткунпоенук; буква а при шифровании перешла в з, ф в х;
г) T =ьтбрызьшюрюыьбр, буква а при шифровании перешла в г, ф в х.
3.Зашифровать слово Архангельск шифром Хилла с ключом A, B = 
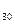, соответствие между буквами русского языка и элементами кольца классов-вычетов Z такие же, как в примере 1. Найти ключ для расшифрования этого шифра, если:
а) A =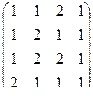 
; б) A = 
; в) A =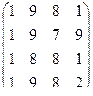 
; г) A = 
.
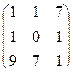4.3. Проблема дискретного логарифмирования
Для создания современных шифров, стойких к различным криптоатакам, создатели шифров используют серьезный математический аппарат. В частности, во многих шифрах используется теорема о том, что мультипликативная группа конечного поля является циклической. Если поле имеет большой порядок, то возникает проблема дискретного логарифмирования.
Пусть G – мультипликативная группа, b и y – некоторые элементы группы G, связанные равенством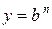 
при некотором целом n. Любое целое x, удовлетворяющее уравнению 
, называется дискретным логарифмом элемента y по основанию b. Задача дискретного логарифмирования в группе G состоит в отыскании по данным y и b некоторого дискретного логарифма х.
|
|
|
Задача определения дискретного логарифма элемента конечной группы может быть легко решена, если порядок группы не слишком велик и для этой группы составлена таблица индексов (см. пример построения таблицы индексов в разделе 2.8). При отыскании дискретного логарифма положительного действительного числа, если нет таблицы индексов, можно воспользоваться методом последовательного приближения. Но в конечном поле нельзя построить метод вычисления дискретного логарифма, подобный данному методу.
Если b имеет бесконечный порядок, то дискретный логарифм любого элемента по основанию b определен однозначно. В противном случае все дискретные логарифмы y по основанию b можно получить из некоторого такого дискретного логарифма 
по формуле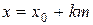 
, где m - порядок элемента b, а параметр k пробегает Z.
Для криптографических приложений наиболее важна задача дискретного логарифмирования в мультипликативных группах конечных полей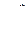 
. Как известно, группа 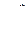циклическая и имеет порядок q -1, поэтому если в качестве b берется некоторый порождающий элемент этой группы, то дискретный логарифм любого элемента 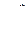по основанию b существует и определен однозначно по модулю q -1.
|
|
|
Дискретный логарифм составляет основу целого ряда алгоритмов криптографии. Дискретный логарифм применяется:
– в криптосистеме с открытым ключом по Диффи - Хеллману;
– DSA – алгоритме цифровой подписи;
– криптосистеме Эль - Гамаля.
Вычислить степень целого числа, то есть произвести умножение его самого на себя любое число раз, можно довольно просто. Однако трудно найти показатель степени, в которую нужно возвести заданное число, чтобы получить другое, тоже заданное. Поэтому задача дискретного логарифмирования имеет высокую вычислительную сложность, чем и объясняется криптостойкость данных алгоритмов.
Дата добавления: 2019-02-12; просмотров: 292; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!