Проверочная матрица линейного кода

 

Будем считать, что символы, из которых состоят исходное и кодовое сообщения, являются элементами некоторого конечного поля F_q, где q – мощность поля. Также будем считать, что шум заключается в замене некоторых символов на другие элементы поля F_q, что эквивалентно добавлению к кодовому вектору x = (x ₁ , x ₂ , …, x_n), поступающему в канал, вектора ошибок e = (e ₁ , e ₂ , …, e_n). Для исправления ошибок такого рода используются линейные коды. Исходное сообщение разбивается на блоки по k символов, и каждый блок (a ₁ , a ₂ , …, a_k) заменяется на соответствующий ему кодовый вектор (x ₁ , x ₂ , …, x_n) длины n > k, в котором k позиций – информационные, то есть 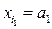, , 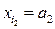…, , 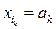а остальные n–k позиций – проверочные, и определяются из системы уравнений:

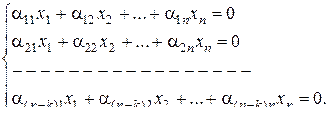                       (1)

Матрица H=(a_ij) коэффициентов системы (1) называется проверочной матрицей линейного (n, k) кода и однозначно определяет множество кодовых векторов, являющееся правым нуль-пространством матрицы H. Код называется систематическим, если первые k символов являются информационными: 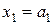, , 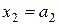…, , 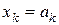а последние n-k символов – проверочными. 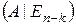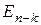Проверочная матрица систематического кода элементарными преобразованиями строк приводится к виду H = , где – единичная матрица размерности n-k.

Систему (1) можно переписать в матричном виде:

 

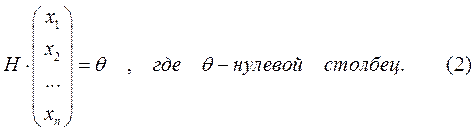
Пусть Н – матрица размерности (n - k)´n и ранга n - k с элементами из поля F_q. Множество С всех n– мерных векторов над F_q, удовлетворяющих равенству (2), называется линейным (блоковым) кодом над F_q блоковой длины n, а также линейным ( n , k ) – кодом. Матрица Н является проверочной матрицей кода С. Если q=2, то С называют бинарным (или двоичным) кодом. Число k / n называют скоростью передачи (или информационной скоростью).

Пример 1. Пусть q = 2, n = 6, k = 3, H = .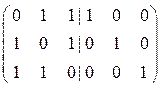

Сообщение (а₁ а ₂ а₃) кодируется вектором х = (а₁ а₂ а₃ х₄ х₅ х₆), то есть 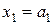, , 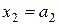, 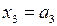а проверочные символы х₄, х₅, х₆ находятся из системы линейных уравнений, заданной проверочной матрицей H.

Имеем систему уравнений: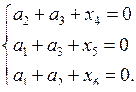

Поэтому х₄ = а₂+а₃, х₅ = а₁+а₃ , х₆ = а₁+а₂.

Если передано сообщение а = 011, то соответствующим кодовым вектором будет х = 011011. Всего имеется 2³ кодовых векторов:

000000, 011011, 110110, 001110,

100011, 111000, 010101, 101101.

 

Порождающая матрица линейного кода

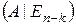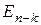Пусть проверочная матрица имеет вид H = , где – единичная матрица размерности n - k. В этом случае из соответствующей СЛУ получим:

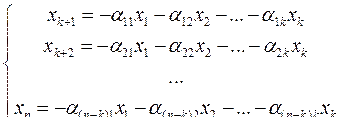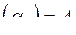, где     (3)

Учитывая, что x₁=a₁, x₂=a₂, …, x_k=a_k, из системы уравнений (3) получим:

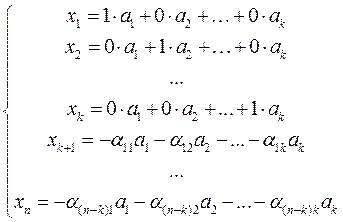
Перепишем в матричном виде:

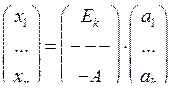. Транспонируя, получим:

Матрица 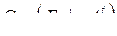 называется порождающей матрицей систематического линейного (n , k)-кода с проверочной матрицей H = .

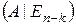Свойства порождающей матрицы:

1. Все кодовые слова можно получить, умножая информационный вектор на матрицу G.

(a₁, a₂, …, a_k) ∙ G = (x₁, x₂, …, x_n) 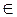 C.

2. Строки матрицы G являются кодовыми словами.

Пусть .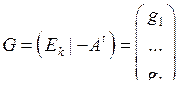

Рассмотрим информационный вектор (a₁, a₂, …, a_k) = (1, 0, …, 0)

(1, 0, …, 0) ∙ G = g₁ , и по свойству 1 g₁Î C.

Аналогично (0, 1, …, 0) ∙ G = g₂ Î C,…, (0, 0, …, 1) ∙ G = g _k Î C .

3. Любая линейная комбинация строк матрицы G является кодовым словом, и наоборот.

 (a₁, a₂, …, a_k) ∙ G = a₁ ∙ g₁ + a₂ ∙ g₂ + … + a_k ∙ g_k Î C по свойству 1.

Таким образом, С = L(g₁, g₂, …, g_n) – линейная оболочка векторов g₁, …, g_k.

4. Строки матрицы G линейно независимы.

Так как в начале матрицы G стоит единичная матрица, то её строки образуют ступенчатую систему, а значит, g₁, g₂,…, g_k  линейно независимы. Из свойств 3 и 4 следует свойство 5.

5. Строки матрицы G g₁, g₂,…, g_k образуют базис линейного пространства кода С.

6. В общем случае, порождающей матрицей линейного ( n , k )-кода С называется любая k× n матрица G , строки которой образуют базис пространства C кодовых слов.

Пример 2. Дана проверочная матрица 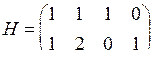 линейного (4,2)-кода над полем F₃ = {0,1,2}.

Напомним, что поле F₃ изоморфно полю классов вычетов по модулю 3, и поэтому 1+2=0 и -1=2, -2=1.

Скорость передачи данного кода  k/n = 2/4 = ½

Матрица H имеет вид:  H = . Найдём порождающую матрицу G по формуле .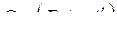

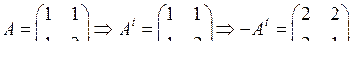, откуда .

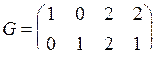Составим таблицу кодирования. Всего может быть 9 различных информационных сообщений (a₁,a₂): 00, 01, 02, 10, 11, 12, 20, 21, 22. Они записаны в первых двух столбцах таблицы. Соответствующие им кодовые векторы находим, умножая информационное сообщение на матрицу G:

(a₁ a₂) ∙ 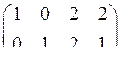 = (x₁ x₂ x₃ x₄)

Информ.сообщ.		Код С
a1	a2	x1	x2	x3	x4
0	0	0	0	0	0
0	1	0	1	2	1
0	2	0	2	1	2
1	0	1	0	2	2
1	1	1	1	1	0
1	2	1	2	0	1
2	0	2	0	1	1
2	1	2	1	0	2
2	2	2	2	2	0

Аналогичные результаты можно получить, записав систему проверочных уравнений, определяемую матрицей Н, и учитывая, что 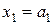,  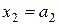– информационные символы:

.

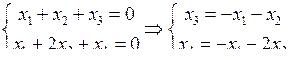В качестве порождающей матрицы этого же кода можно взять матрицу G= 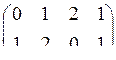, строки которой – линейно независимые векторы из С. При этом изменится соответствие между информационными сообщениями и кодовыми векторами, а множество кодовых векторов С будет таким же (проверьте самостоятельно).

 

---

Дата добавления: 2019-02-12; просмотров: 2105; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!