Общие свойства линейных кодов. Коды Хэмминга
Теорема 4. Пусть Н – проверочная матрица (n , k) – кода С. Если любые d-1 столбцов матрицы H линейно независимы, но существуют d линейно зависимых столбцов, то dmin(C) = d. □
Чтобы проверить существование линейных (n,k) – кодов над Fq с минимальным расстоянием ≥ d , достаточно показать, что существует (n-k)´n - матрица Н, удовлетворяющая условию из теоремы 4 при s = d -1.
Теорема 5. (Граница Гилберта - Варшамова).
Если qn-k >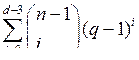 
, то над Fq можно построить линейный (n , k) – код с минимальным расстоянием ≥ d.
Доказательство.
Построим для такого кода проверочную ( n - k ) ´ n - матрицу Н. В качестве первых n - k столбцов выберем n - k линейно независимых векторов из F n-kq . Это дает равенство rank H = n-k и , так как d – 1 ≤ n-k в силу теоремы 6 3), обеспечивает условия для следующего индуктивного шага. Пусть уже выбраны g-1 столбцов так, что любые d-1 из них линейно независимы. Имеется самое большее
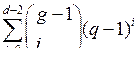
векторов в Fqn-k, являющихся линейными комбинациями не более чем d-2 столбцов из g-1 выбранных. Если неравенство в условии теоремы выполнено, то можно выбрать g–й столбец, который линейно независим с любыми d-2 столбцами из ранее выбранных. Тот факт, что для полученного кода dmin ≥ d, следует из теоремы 4 с учетом того, что любые d-1 столбцов в Н линейно независимы. □
Пусть С – линейный (n,k) – код над Fq, содержащий кодовое слово с ненулевой i-й координатой. Пусть D - подпространство в С, состоящее из всех кодовых слов с i–й координатой, равной 0. Размерность D на единицу меньше размерности С, т.е.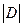 
= qk-1. Очевидно, каждый из q смежных классов фактопространства С/D содержит кодовые слова с одним и тем же значением i–й координаты, и эти значения различны для различных классов. Таким образом, для каждого α 
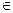Fq имеется qk-1 кодовых слов х с хi = α. Если составить матрицу с кодовыми словами в качестве строк, то любой ненулевой столбец этой матрицы содержит (q-1)×qk-1 ненулевых элементов. Поэтому сумма весов кодовых слов из С ограничена числом nqk-1(q-1). Общее число кодовых слов ненулевого веса равно qk-1 . Так как минимальное расстояние кода равно минимальному ненулевому весу, оно не превосходит среднего веса ненулевых кодовых слов. Тем самым доказана следующая теорема.
|
|
|
Теорема 5 (граница Плоткина). Если имеется линейный код над Fq длины n с М кодовыми словами и минимальным расстоянием d, то
d ≤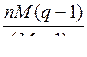 
.
Пусть С – код над Fq длины n с М кодовыми словами. Предположим, что С может исправлять t ошибок. Имеется (q-1)m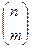 
векторов длины n и веса m над Fq. Шары радиуса t с центрами в кодовых словах не пересекаются, и каждый из М шаров содержит
1+(q-1)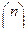 
+…..+(q-1)t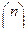 
векторов. Общее число векторов в Fqn равно qn. Отсюда вытекает следующий факт.
|
|
|
Теорема 6 (граница Хэмминга). Параметры q, n, t, M кода над Fq длины n с М кодовыми словами, исправляющего t ошибок, удовлетворяют неравенству:
M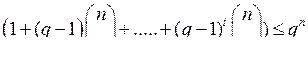 
.
В случае, когда все векторы из Fqn лежат в шарах радиуса t с центральными в кодовых словах линейного (n,k) – кода, мы получаем специальный класс кодов.
Код над Fq, исправляющий t ошибок, называется совершенным, если в теореме 6 достигается равенство.
Бинарный код С m длины n = 2m – 1, m ≥ 2, с проверочной матрицей Н, столбцами которой служат все ненулевые бинарные векторы длины m , называется бинарным кодом Хэмминга.
Из теоремы 4 следует, что Сm имеет минимальное расстояние 3, а значит, может исправлять ошибки с весом w(e) = 1 и обнаруживать ошибки с весом w(e) = 2.
Декодирование кодов Хэмминга особенно просто. Выберем лексикографический порядок для столбцов в Н; тогда i-й столбец будет бинарной записью числа i. Если ошибка возникает в i–й координате, то синдром принятого вектора y S( y ) = HyT = HeT будет бинарной записью номера позиции ошибки i.
Пример: Рассмотрим (7,4,3) – код Хэмминга С3 с проверочной матрицей
Н =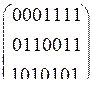 
.
Первый столбец есть бинарная запись числа 1 = (001)Т, второй столбец есть 2 = (010)Т и т.д.
Пусть получен у=(1100010), тогда S ( y ) = (101)T, и мы знаем, что ошибка возникла в пятой координате, так как (101) - бинарная запись числа 5.
|
|
|
у=(1100010) декодируем в вектор х=(1100110).
Если получен y=(1011011), тогда S ( y )=(111)T, ошибка возникла в седьмой координате, поэтому х=(1011010).
Дата добавления: 2019-02-12; просмотров: 465; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!