АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ В АЛГЕБРАИЧЕСКОЙ ГЕОМЕТРИИ
1.3. Алгебраические структуры в алгебраической геометрии
Алгебраическая геометрия является одним из самых трудных и, одновременно, одним из самых динамично развивающихся направлений фундаментальной математики. Это – область математики, объединяющая геометрию и алгебру. В широком смысле слова основным предметом изучения как в классической, так и в современной алгебраической геометрии являются множества решений систем уравнений, задаваемых многочленами. В узком смысле алгебраическая геометрия изучает геометрические объекты, связанные с алгебраическими структурами (главным образом – коммутативными кольцами).
Основным объектом изучения классической алгебраической геометрии являются алгебраические многообразии, по сути –геометрические объекты, которые задаются множествами решений системы многочленных уравнений. Наиболее хорошо к настоящему времени изучены алгебраические кривые – прямые, а также квадрики, кубики (например, эллиптическая кривая), квартики (например, овалы Кассини).
Для современной алгебраической геометрии характерно множество взаимосвязей с различными областями математики – комплексным анализом, топологией, теорией чисел и др. Зарождаясь как поиски способов для решения вполне конкретных уравнений, алгебраическая геометрия в дальнейшем обратилась к изучению свойств, являющихся внутренними для множества решений достаточно произвольной системы полиномиальных уравнений, что в итоге приводит к разнообразным задачам из ряда других разделов математики. Таким образом, в XX столетии алгебраическая геометрия естественным образом разделилась на несколько подразделов:
· основным направлением для алгебраической геометрии является изучение свойств различных алгебраических многообразий над алгебраически замкнутым полем (например, над полем комплексных чисел C).
· Арифметическая (или диофантова) геометрия – раздел алгебраической теории чисел, изучающий «алгебраические многообразия» над полем, являющимся алгебраическим числовым полем (или даже над кольцом).
· Действительная геометрия, занимающаяся изучением действительных точек комплексных многообразий.
· Изучение особенностей различных алгебраических многообразий – наиболее весомая часть теории особенностей.
· На стыке информатики с алгебраической геометрией располагается вычислительная алгебраическая геометрия. Основная задача вычислительной алгебраической геометрии – создание различных алгоритмов, помогающих изучать свойства алгебраических многообразий, заданных явным образом.
Рассмотрим историю развития алгебраической геометрии.
Первые признаки появления алгебраической геометрии можно обнаружить в работах древних греков (V век до н. э.). К примеру, проблема об удвоении куба редуцируется к построению куба, у которого объем является равным объёму «ящика» a´a´b при заданных a и b. Менехм переформулировал эту задачу геометрическим образом как задачу о построении пересечения двух коник, задаваемых уравнениями ay = x2 и xy = ab. В появившихся позднее трудах таких ученых, как Архимед и Аполлоний, конические сечения подвергаются более систематическому изучению, в том числе и с использованием координатных рассуждений. Арабским математикам были известны способы решения для определённых кубических уравнений и они могли переформулировать получаемые результаты на геометрическом языке. Персидский математик и поэт Омар Хайям (XI век) обнаружил способ решения для общего кубического уравнения с помощью пересечения окружности с параболой. Французские ученые Франсуа Виет, Рене Декарт и Пьер Ферма кардинальным образом изменили способы геометрических построений, основав аналитическую геометрию. Их главной целью являлось изучение так называемых алгебраических кривых, таких как кривые, задаваемые диофантовыми уравнениями, а также коники и кубики. Приблизительно в тот же самый период Дезарг и Паскаль, развив проективную геометрию, подобрались к этой проблеме с иной стороны. Они также изучали свойства кривых, правда с точки зрения геометрии, благодаря использованию построений циркулем и линейкой. В итоге, аналитическая геометрия оказалась предпочтительнее этого подхода, поскольку снабжала математиков в XVIII веке вполне конкретным вычислительным инструментарием, позволяющим решать задачи физического характера с использованием нового анализа. Тем самым, к периоду конца XVIII столетия использование в геометрии алгебраических методов сводилось главным образом к задействованию исчисления бесконечно малых (в том числе активно использовавшегося Эйлером и Лагранжем). В XIX веке развитие таких направлений, как неевклидова геометрия и теория абелевых интегралов содействовало возвращению в геометрию алгебраических идей. Кэли первым изучал однородные многочлены на проективном пространстве, в частности, он исследовал квадратичные формы. В дальнейшем Феликс Клейн изучал проективную геометрию (а также ряд других разделов геометрии) с той позиции, что группа преобразований определяет геометрию пространства. В конце XIX столетия геометры исследовали не только линейные проективные преобразования, но также и так называемые «бирациональные преобразования более высокой степени».
Бернхард Риман создал теорию римановых многообразий в процессе развития теории абелевых интегралов. Задействовав интегралы первого рода, К. Шварц показал: кривая, допускающая непрерывную группу бирациональных преобразований в себя, бирационально эквивалентна эллиптической кривой или прямой. Во второй половине XIX столетия алгебраическая геометрия была представлена, в основном, итальянскими математиками от Кремоны и до Энриквеса. В тот период стартовала алгебраизация геометрии путем использования коммутативной алгебры: в том числе, Д. Гильберт доказал свои знаменитые теоремы – теорему о базисе и «Nullstellensatz».
Мысли о построении алгебраической геометрии на фундаменте коммутативной алгебры, развивавшейся интенсивно в 30-х–40-х годах XX столетия, впервые появились у О. Зарисского и А. Вейля. Одной из целей этих ученых было доказательство различных результатов итальянской школы алгебраической геометрии: итальянские геометры в то время использовали в рассуждениях понятие «общей точки», причем, не давая строгого определения такой точки. В 1950-х–60-х годах Ж.-П. Серр, а также А. Гротендик переработали полностью основания всей алгебраической геометрии при помощи конструкций теории пучков, гомологической алгебры и теории схем. В 1970-х годах развитие в определенной степени стабилизировалось, и были найдены приложения алгебраической геометрии к теории чисел, а также к классическим проблемам алгебраической геометрии: изучению модулей и особенностей.
Абелевы многообразия являются важным классом алгебраических многообразий, которые довольно трудно описать только при помощи одних определяющих уравнений. Основной пример таких многообразий – эллиптические кривые, имеющие весьма обширную теорию. Они явились инструментом доказательства Большой теоремы Ферма и широко используются для нужд эллиптической криптографии. Алгебраическая геометрия имеет приложения в теории управления, статистике, теории кодирования, моделировании и робототехнике. Также известны приложения в теории игр, струн, теории паросочетаний и солитонов.
Аффинные многообразия.
Зафиксируем основное поле k. В классической алгебраической геометрии, используется, как правило, поле комплексных чисел, тем не менее, многие результатов остаются верны для всякого алгебраически замкнутого поля (в дальнейшем будем подразумевать алгебраическую замкнутость). Рассмотрим далее n-мерное аффинное пространство An (причина, в силу которой рассматривается не векторное пространство над полем k, состоит в том, чтобы отметить независимость различных свойств многообразия от самой структуры этого векторного пространства. Элементы из основного пространства рассматриваются не как вектора, а как точки). Зафиксируем теперь в аффинном пространстве какой-то базис (в том числе, выберем точку О – начало координат). Тогда для каждого семейства S многочленов кольца k[x1,…,xn] мы можем сопоставить некоторое множество V(S) таких точек, чьи координаты удовлетворяют всем без исключения многочленам из данного множества: V(S) = {(t 1 ,…, tn) |"pÎS, p(t 1 ,…, tn)=0}.
Поскольку, полиномиальность функции – свойство, не зависящее от выбора базиса, то можно говорить и о полиномиальных функциях на An и о множестве общих нулей для семейства данных функций. Множества, которые представимы в виде V(S), называются обычно алгебраическими множествами.
Для всякого подмножества аффинного пространства U мы можем сопоставить множество таких многочленов, которые равны нулю во всех точках этого множества. Несложно проверить, что такое множество является идеалом в нашем кольце многочленов (Идеалом кольца R называется такое подкольцо, которое замкнуто относительно умножения на элементы из R, идеал обычно обозначается символом I). Возникают два вполне естественных вопроса:
· Какие множества U удовлетворяют равенству U = V(I(U))?
· Какие множества многочленов S удовлетворяют равенству S = I(V(S))?
Нетрудно видеть, что необходимым условием выполнимости первого равенства является алгебраичность множества U; также нетрудно проверить, что это условие и достаточно. Нахождение ответа на второй вопрос представляет собой серьезные трудности, согласно упомянутой выше теореме Nullstellensatz.
I(V(S)) в точности совпадает с радикалом идеала в нашем кольце многочленов, порождённого элементами S; это означает, что имеет место биективное соответствие между радикальными идеалами кольца и алгебраическими множествами (Радикалом идеала I называется идеал, образованный всеми такими элементами x, что некоторая степень таких x принадлежит самому I. Радикальным идеалом называется идеал, который совпадает со своим собственным радикалом.) В теореме Гильберта о базисе утверждается, что все идеалы кольца многочленов –конечнопорождённые, по-другому говоря, всякое алгебраическое множество мы можем задать при помощи конечного числа уравнений.
Алгебраическое множество называют неприводимым, если его невозможно представить как объединение двух меньших алгебраических множеств.
Аффинным алгебраическим многообразием называютнеприводимое алгебраическое множество; на языке алгебры аффинным многообразиям соответствуют простые идеалы в кольце многочленов. (Идеал I в коммутативном кольце A называют простым, если факторкольцо по I есть область целостности.) Спектром коммутативного кольца R называется множество всех простых идеалов этого кольца. Обычно спектр снабжают топологией Зарисского (определение будет дано ниже) а также пучком коммутативных колец, что превращает его в локально окольцованное пространство. Спектр кольца R обозначают Spec R. Всякое алгебраическое множество мы можем представить в виде объединения некоторого конечного числа алгебраических многообразий (ни одно из которых не может быть подмножеством другого), и притом только единственным образом. Некоторые специалисты не проводят чётких различий между алгебраическими множествами и алгебраическими многообразиями и называют алгебраические множества неприводимыми алгебраическими множествами (или неприводимыми многообразиями).
Регулярные функции.
Регулярной функцией на алгебраическом множестве VÌAn называется функция, которая является ограничением некоторой полиномиальной функции на V . Функции, регулярные на V,образуют структуру − кольцо k[V], которое называется координатным кольцом данного множества. Такое кольцо изоморфно факторкольцу кольца многочленов по I(V) (в действительности, если f и g одинаковое ограничение на V, то f − g принадлежит I(V).)
Естественным путем определяются и регулярные отображения между различными алгебраическими множествами: регулярное отображение f : X® An представимо в виде (f 1 , f 2 ,… fn), где все fi есть регулярные функции. Регулярное отображение в алгебраическое множество YÎAn есть регулярная функция f : X® An, такая что f ( X ) Í Y . Если у нас задано регулярное отображение f : X® Y, то всякой регулярной функции j: Y® A 1 мы можем сопоставить определенную регулярную функцию на f * j : X® A 1 по закону f * j = j◦f . Морфизм j®j◦f есть гомоморфизмом колец f * : k[Y] ® k[X], так же в точности и всякий гомоморфизм между координатными кольцами задает регулярное отображение алгебраических множеств (но в обратном направлении).
Рациональные функции.
Пусть A является коммутативной областью целостности и пусть A * = A\{0}. Рассмотрим тогда множество всех упорядоченных пар A´A * ={(n , m)| n Î A , m Î A *}. Две упорядоченные пары (n , m) и (s,t) мы будем считать эквивалентными, если выполняется равенство nt = ms . Множество всех классов эквивалентности на A´A * мы обозначим через Q ( A ) . Определим на множестве Q ( A ) операции сложения и умножения, согласно следующим правилам:
1. 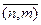 ×
× 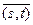 =
= 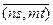 ,
,
2. 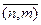 +
+ 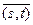 =
= 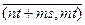 , где под
, где под 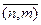 понимается класс эквивалентности для элемента (n , m). Множество Q ( A ) с данными операциями называется полем отношений (полем частных) кольца A . Построенное множество Q ( A ) есть поле, нулевым элементом которого является
понимается класс эквивалентности для элемента (n , m). Множество Q ( A ) с данными операциями называется полем отношений (полем частных) кольца A . Построенное множество Q ( A ) есть поле, нулевым элементом которого является 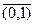 , а единичным −
, а единичным − 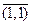 .
.
Пример. Поле рациональных чисел Q − есть ни что иное, как поле частных Q ( Z ) для кольца целых чисел Z.
Если V является аффинным многообразием, то его координатное кольцо является целостным (областью целостности), и тем самым, имеет и поле частных. Данное поле обозначается k(V) и называется полем рациональных функций на V. Область определения у рациональной функции совсем не обязательно равна всему V, она равна дополнению множества, на котором знаменатель этой функции обращается в ноль. Как и в случае регулярных функций, мы определяем рациональное отображение между многообразиями, при этом рациональные отображения соответствуют взаимно-однозначно гомоморфизмам полей рациональных функций.
Два аффинных многообразия мы называем бирационально эквивалентными, если имеются два рациональных отображения между данными многообразиями, взаимно обратные на областях определения (эквивалентная формулировка: поля рациональных функций для этих многообразий являются изоморфными). Аффинное многообразие мы называем рациональным многообразием , если данное многообразие бирационально эквивалентно аффинному пространству. Другими словами, такое многообразие мы можем рационально параметризовать.
К примеру, единичная окружность представляет собой рациональную кривую, поскольку существуют функции
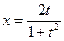 ,
, 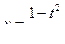 , которые задают рациональное отображение прямой в окружность, при этом можно проверить, что обратное отображение также рационально.
, которые задают рациональное отображение прямой в окружность, при этом можно проверить, что обратное отображение также рационально.
Пучки и схемы.
Центральным понятием алгебраической геометрии является понятие пучка. Выдающийся французский математик Жан Лере придумал пучки, находясь в застенках фашистского концлагеря времен Второй мировой войны. В научный оборот понятие пучка было введено Жаном-Пьером Серром в работе [23]. Пучки, разновидности пучков – расслоения и их инварианты составляют в наше время основу геометрической науки. Свойства пучков автоматизируют свойства тензорных полей на многообразиях. Пучкам отвечают коммутативные группы, называемые группами когомологий со значениями в пучке, и специальные элементы групп когомологий многообразия со значениями в постоянном пучке, называемые классами Черна. Группы когомологий и классы Черна определяют важнейшие фундаментальные свойства многообразия (о группах когомологий и классах Черна см., например, в [21], [26]).
Эти понятия являются основным языком всех разделов современной геометрии. Понятие пучка дает систематический способ согласования локальных алгебраических данных на топологическом пространстве. Например, регулярные функции на открытых подмножествах многообразия образуют пучок. Пучки являются основным инструментом при изучении схем. В действительности даже само понятие схемы нельзя определить без использования пучков.
Пусть X – топологическое пространство.
Предпучок абелевых групп F на X состоит из следующих объектов: абелевой группы F ( U ) для каждого открытого подмножества U Ì X и гомоморфизма абелевых групп r uv : F ( U ) ® F ( V ) для каждого вложения открытых подмножеств V Ì U в X, удовлетворяющих условиям:
0) F(Æ)=0, где Æ – пустое множество;
(1) r uv : F ( U ) ® F ( V ) – тождественное отображение;
(2) если W Ì V Ì U , то ruw=rvw  ruv.
ruv.
Элементы F ( U ) называются сечениямипучка F над открытым множеством U; для F ( U ) иногда также используется обозначение Г( U , F ).
Отображения r uv называются отображениями ограничения; иногда вместо r uv ( s ) можно писать s  v , если s Î F ( U ).
v , если s Î F ( U ).
Пучок – это, грубо говоря, предпучок, сечения которого определяются локально. Точнее, введем следующее определение.
Предпучок F на топологическом пространстве X называется пучком, если он удовлетворяет следующим дополнительным условиям:
(3) пусть U – открытое множество, {Vi} – его открытое покрытие и s Î F ( U ) – такой элемент, что s  vi=0 для всех i; тогда s =0;
vi=0 для всех i; тогда s =0;
(4) пусть U – открытое множество, {Vi} – его открытое покрытие, и пусть для каждого i задан элемент si Î F ( Vi ), такой, что si  vi
vi 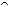 vj = sj
vj = sj  vi
vi 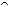 vj для любых i , j; тогда существует элемент s Î F ( U ), такой, что s
vj для любых i , j; тогда существует элемент s Î F ( U ), такой, что s  vi = si для каждого i . (Отметим, что из условия (3) следует единственность элемента s)
vi = si для каждого i . (Отметим, что из условия (3) следует единственность элемента s)
Замечание. Согласно нашему определению, пучок – это предпучок, удовлетворяющий дополнительным условиям. В некоторых книгах дается эквивалентное определение пучка как топологического пространства над X с некоторыми свойствами.
Приведем несколько примеров.
Пусть X – многообразие над полем k . Для каждого открытого множества U Ì X пусть O ( U ) – кольцо регулярных функций на U со значениями в k, и для каждого V Ì U пусть r uv : O ( U ) ® O ( V ) – отображение ограничения. Тогда O является пучком колец на X. Действительно, очевидно, что он является предпучком колец. Для того, чтобы проверить условия (3) и (4), заметим, что функция, которая является нулевой и локально регулярная функция является всюду регулярной. Пучок O будем называть пучком регулярных функцийна X.
Точно таким же образом можно определить пучок непрерывных вещественных функций на любом топологическом пространстве, пучок дифференцируемых функций на дифференцируемом многообразии или пучок голоморфных функций на комплексном многообразии.
Пусть X – топологическое пространство и A – абелева группа. Тогда на X посредством A можно определить постоянный пучок А следующим образом. Наделим А дискретной топологией и для каждого открытого множества UÌX обозначим через А( U ) группу всех непрерывных отображений из U в А. Тогда вместе с обычными отображениями ограничения набор групп А( U ) задает пучок А. Отметим, что для каждого связного открытого множества U имеет место изоморфизм А(U) 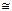 А, что объясняет термин «постоянный пучок». Если U – открытое множество, компоненты связности которого открыты (что всегда выполнено для локально связного топологического пространства), тоА( U ) является прямым произведением экземпляров группы А в числе, равном числу связных компонент множества U .
А, что объясняет термин «постоянный пучок». Если U – открытое множество, компоненты связности которого открыты (что всегда выполнено для локально связного топологического пространства), тоА( U ) является прямым произведением экземпляров группы А в числе, равном числу связных компонент множества U .
Слой Fp предпучка F на U в точке P 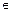 X определим как прямой предел групп F(U) по всем открытым множествам U, содержащим P, относительно отображений ограничения
X определим как прямой предел групп F(U) по всем открытым множествам U, содержащим P, относительно отображений ограничения 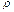 .
.
Таким образом, элемент слоя Fp представляется парой 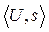 , где U – открытая окрестность точки P и s – элемент группы F(U) . Две такие пары
, где U – открытая окрестность точки P и s – элемент группы F(U) . Две такие пары 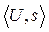 ,
, 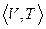 определяют один и тот же элемент слоя Fp , если и только если существует такая открытая окрестность W точки P, W
определяют один и тот же элемент слоя Fp , если и только если существует такая открытая окрестность W точки P, W  U
U  V, что s
V, что s  w= t
w= t  w. Значит, можно сказать, что элементы слоя Fp – это ростки сечений пучка F в точке P. Слой пучка регулярных функций O на многообразии X – это не что иное, как локальное кольцо Op в точке P на X.
w. Значит, можно сказать, что элементы слоя Fp – это ростки сечений пучка F в точке P. Слой пучка регулярных функций O на многообразии X – это не что иное, как локальное кольцо Op в точке P на X.
Морфизмом  : F
: F  G предпучков F и G на X называется набор гомоморфизмов абелевых групп
G предпучков F и G на X называется набор гомоморфизмов абелевых групп  (U): F(U)
(U): F(U)  G(U) по одному для каждого открытого множества U, таких, что для всякого вложения открытых множеств V
G(U) по одному для каждого открытого множества U, таких, что для всякого вложения открытых множеств V  U следующая диаграмма:
U следующая диаграмма:
F(U) 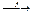 G(U)
G(U)
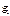
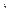
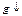
F(V) 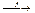 G(V)
G(V)
коммутативна ( 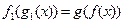 ), где вертикальные морфизмы — отображения ограничения для F и G соответственно. В случае, когда F и G - пучки на X,
), где вертикальные морфизмы — отображения ограничения для F и G соответственно. В случае, когда F и G - пучки на X,  называется морфизмом пучков. Морфизм
называется морфизмом пучков. Морфизм  называется изоморфизмом, если для него существует левый и правый обратные морфизмы.
называется изоморфизмом, если для него существует левый и правый обратные морфизмы.
Отметим, что морфизм предпучков  : F
: F  G индуцирует морфизм слоев
G индуцирует морфизм слоев  p: F p
p: F p  Gp для любой точки P
Gp для любой точки P 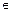 X. Следующее предложение (которое не имеет места для предпучков) иллюстрирует локальную природу пучков.
X. Следующее предложение (которое не имеет места для предпучков) иллюстрирует локальную природу пучков.
Предложение. Морфизм пучков  : F
: F  G на топологическом пространстве X тогда и только тогда является изоморфизмом, когда индуцированный им морфизм слоев
G на топологическом пространстве X тогда и только тогда является изоморфизмом, когда индуцированный им морфизм слоев  p: F p
p: F p  Gp является изоморфизмом для каждой точки P
Gp является изоморфизмом для каждой точки P 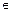 X.
X.
Доказательство. Если  изоморфизм, то ясно, что
изоморфизм, то ясно, что  p является изоморфизмом для любой точки P
p является изоморфизмом для любой точки P 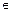 X. Обратно, предположим, что
X. Обратно, предположим, что  p является изоморфизмом для всех точек P
p является изоморфизмом для всех точек P 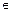 X. Для того, чтобы доказать, что
X. Для того, чтобы доказать, что  - изоморфизм, достаточно показать, что
- изоморфизм, достаточно показать, что  (U): F(U)
(U): F(U)  G(U) является изоморфизмом для всякого открытого множества U, поскольку тогда можно определить обратный морфизм
G(U) является изоморфизмом для всякого открытого множества U, поскольку тогда можно определить обратный морфизм 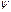 , полагая, что
, полагая, что 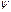 (U)=
(U)=  (U)-1 для каждого U. Докажем сначала инъективность
(U)-1 для каждого U. Докажем сначала инъективность  (U). Пусть s
(U). Пусть s 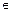 F(U), и предположим, что
F(U), и предположим, что  (s)
(s) 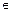 G(U) равен 0. Тогда для каждой точки P
G(U) равен 0. Тогда для каждой точки P 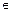 U образ
U образ  (s)p элемента
(s)p элемента  (s) в слое Gp равен 0.Так как отображение
(s) в слое Gp равен 0.Так как отображение  p инъективно для любой точки P, то отсюда следует, что sp =0 в F p для каждой точки P
p инъективно для любой точки P, то отсюда следует, что sp =0 в F p для каждой точки P 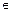 U. Утверждение sp =0 означает, что s и 0 имеют один и тот же образ в Fp , а это означает в свою очередь, что существует открытая окрестность Wp точки P, Wp
U. Утверждение sp =0 означает, что s и 0 имеют один и тот же образ в Fp , а это означает в свою очередь, что существует открытая окрестность Wp точки P, Wp  U, такая, что s
U, такая, что s  Wp =0. Множество U покрывается такими окрестностями Wp всех его точек P, так что по свойству пучков (3) элемент s равен 0 на U. Это доказывает инъективность
Wp =0. Множество U покрывается такими окрестностями Wp всех его точек P, так что по свойству пучков (3) элемент s равен 0 на U. Это доказывает инъективность  (U).
(U).
Покажем теперь, что  (U) сюръективно. Пусть t
(U) сюръективно. Пусть t 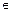 G(U) и tp – его росток в точке P
G(U) и tp – его росток в точке P 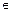 U. Так как отображение
U. Так как отображение  p сюръективно, то существует элемент sp
p сюръективно, то существует элемент sp 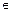 Fp , такой, что
Fp , такой, что  p(sp)= tp. Пусть sp представлен сечением s(P) в некоторой окрестности Vp точки P. Тогда ростки элементов
p(sp)= tp. Пусть sp представлен сечением s(P) в некоторой окрестности Vp точки P. Тогда ростки элементов  (s(P)) и t
(s(P)) и t  Vp совпадают в точке P и, следовательно, заменяя Vp на меньшую окрестность, если в этом есть необходимость, можно считать, что
Vp совпадают в точке P и, следовательно, заменяя Vp на меньшую окрестность, если в этом есть необходимость, можно считать, что  (s(P))= t
(s(P))= t  Vp в G(Vp). Стало быть, U покрывается открытыми множествами Vp и на каждом Vp задано сечение s ( P ) Î F ( Vp ), причем для различных точек P и Q сечения s ( P )
Vp в G(Vp). Стало быть, U покрывается открытыми множествами Vp и на каждом Vp задано сечение s ( P ) Î F ( Vp ), причем для различных точек P и Q сечения s ( P )  Vp
Vp 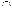 VQ и s ( Q )
VQ и s ( Q )  Vp
Vp 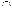 VQ в F ( Vp Ç VQ ) отображаются при j в сечение t
VQ в F ( Vp Ç VQ ) отображаются при j в сечение t  Vp
Vp  VQ . Следовательно, в силу доказанной выше инъективности j эти сечения совпадают на Vp Ç VQ.
VQ . Следовательно, в силу доказанной выше инъективности j эти сечения совпадают на Vp Ç VQ.
По свойству пучков (4) существует сечение s Î F ( U ), такое, что s  Vp = s ( P ) для каждой точки P Î U . Осталось проверить, что j ( s )= t . Для этого заметим, что j(s), t
Vp = s ( P ) для каждой точки P Î U . Осталось проверить, что j ( s )= t . Для этого заметим, что j(s), t  G(U), и для каждой точки P
G(U), и для каждой точки P  U имеем j (s)
U имеем j (s)  Vp = t
Vp = t  Vp. Следовательно, по свойству пучков (3), примененному к сечению j (s) – t, получаем, что j (s)=t.
Vp. Следовательно, по свойству пучков (3), примененному к сечению j (s) – t, получаем, что j (s)=t.
Определим теперь ядра, коядра и образы морфизмов пучков.
Определение 1.1.6. Пусть j: F  G - морфизм предпучков. Определим ядро, коядро и образ j как предпучки, заданные соответственно формулами U
G - морфизм предпучков. Определим ядро, коядро и образ j как предпучки, заданные соответственно формулами U  ker(j (U)), U
ker(j (U)), U  coker(j (U)),
coker(j (U)),
U  im(j (U)).
im(j (U)).
Отметим, что если j: F  G - морфизм пучков, то его ядро тоже является пучком, но коядро и образ пучками, вообще говоря, не являются. Это приводит к необходимости ввести понятие пучка, ассоциированного с предпучком.
G - морфизм пучков, то его ядро тоже является пучком, но коядро и образ пучками, вообще говоря, не являются. Это приводит к необходимости ввести понятие пучка, ассоциированного с предпучком.
Предложение-определение. Для каждого предпучка F существует пучок F+ и морфизм 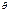 : F
: F  F+ , обладающие следующим свойством: для любого пучка G и любого морфизма
F+ , обладающие следующим свойством: для любого пучка G и любого морфизма  : F
: F  G существует единственный морфизм
G существует единственный морфизм 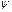 : F+
: F+  G, такой, что
G, такой, что  =
= 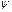

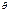 . Кроме того, пара (F+,
. Кроме того, пара (F+, 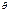 ), единственна с точностью до однозначно определенного изоморфизма. Пучок F+ называется пучком, ассоциированным с предпучком F .
), единственна с точностью до однозначно определенного изоморфизма. Пучок F+ называется пучком, ассоциированным с предпучком F .
Доказательство. Пучок F+ строится следующим образом. Для любого открытого множества U обозначим через F+(U) множество функций s из U в объединение 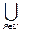 Fp слоев F над точками множества U, таких, что
Fp слоев F над точками множества U, таких, что
(1) s(P) 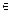 F p для каждой точки P
F p для каждой точки P 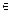 U и
U и
(2) для каждой точки P 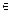 U существует окрестность V, P
U существует окрестность V, P 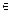 V, содержащаяся в U, и элемент t
V, содержащаяся в U, и элемент t 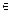 F(V), такие, что для всех Q
F(V), такие, что для всех Q 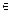 V росток tQ равен s(Q).
V росток tQ равен s(Q).
Непосредственно проверяется, что F+ с естественными отображениями ограничения является пучком, что существует естественный морфизм 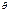 : F
: F  F+ и что выполняется требуемое свойство универсальности. Единственность F+ - это формальное следствие свойства универсальности. Отметим также, что если F - пучок, то F+ изоморфен F, причем изоморфизм осуществляется морфизмом
F+ и что выполняется требуемое свойство универсальности. Единственность F+ - это формальное следствие свойства универсальности. Отметим также, что если F - пучок, то F+ изоморфен F, причем изоморфизм осуществляется морфизмом 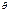 .
.
Подпучком пучка F называется пучок Fˊ , такой, что Fˊ(U) для каждого открытого множества U 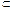 X и отображения ограничения для пучка Fˊ индуцированы отображениями ограничения для пучка F . Отсюда следует, что слой Fˊp является подгруппой в слое Fp для любой точки P.
X и отображения ограничения для пучка Fˊ индуцированы отображениями ограничения для пучка F . Отсюда следует, что слой Fˊp является подгруппой в слое Fp для любой точки P.
Пусть  : F
: F  G - морфизм пучков, тогда ядро
G - морфизм пучков, тогда ядро  , обозначаемое ker
, обозначаемое ker  , определенное выше для морфизма предпучков, является на самом деле пучком и, следовательно, подпучком пучка F.
, определенное выше для морфизма предпучков, является на самом деле пучком и, следовательно, подпучком пучка F.
Будем называть морфизм пучков  : F
: F  G инъективным, если
G инъективным, если
ker  =0, так что
=0, так что  инъективен тогда и только тогда, когда индуцированное отображение
инъективен тогда и только тогда, когда индуцированное отображение  (U): F(U)
(U): F(U)  G(U) инъективно для каждого открытого множества U в X.
G(U) инъективно для каждого открытого множества U в X.
Образом морфизма пучков  : F
: F  G, обозначаемым через im
G, обозначаемым через im  , называется пучок, ассоциированный с предпучком – образом морфизма
, называется пучок, ассоциированный с предпучком – образом морфизма  в категории предпучков. По свойству универсальности пучка, ассоциированного с предпучком, существует естественное отображение im
в категории предпучков. По свойству универсальности пучка, ассоциированного с предпучком, существует естественное отображение im 
 G. В действительности это отображение инъективно, и, следовательно, im
G. В действительности это отображение инъективно, и, следовательно, im  можно отождествить с подпучком пучка G.
можно отождествить с подпучком пучка G.
Будем называть морфизм  : F
: F  G сюръективным, если im
G сюръективным, если im  =G.
=G.
Последовательность пучков и морфизмов
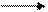
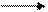
 … F i-1 F i F i+1 …
… F i-1 F i F i+1 …
будем называть точной, если ker  i = im
i = im  i-1 для каждого i.
i-1 для каждого i.
Таким образом, последовательность 0  F
F  G точна тогда и только тогда, когда морфизм
G точна тогда и только тогда, когда морфизм  инъективен, и последовательность F
инъективен, и последовательность F  G
G  0 точна тогда и только тогда, когда
0 точна тогда и только тогда, когда  сюръективен.
сюръективен.
Пусть Fˊ - подпучок пучка F . Определим факторпучок F/ Fˊ как пучок, ассоциированный с предпучком U  F(U)/ Fˊ(U). Из определения следует, что для любой точки P слой (F/ Fˊ)p совпадает с Fp/ Fˊp .
F(U)/ Fˊ(U). Из определения следует, что для любой точки P слой (F/ Fˊ)p совпадает с Fp/ Fˊp .
Определим коядро морфизма пучков  : F
: F  G, обозначаемое через coker
G, обозначаемое через coker  , как пучок, ассоциированный с предпучком – коядром морфизма
, как пучок, ассоциированный с предпучком – коядром морфизма  в категории предпучков.
в категории предпучков.
Выше было отмечено, что морфизм пучков  : F
: F  G инъективен тогда и только тогда, когда отображение сечений
G инъективен тогда и только тогда, когда отображение сечений  (U): F(U)
(U): F(U)  G(U) инъективно для каждого открытого множества U. Соответствующее утверждение для сюръективных морфизмов неверно: если морфизм
G(U) инъективно для каждого открытого множества U. Соответствующее утверждение для сюръективных морфизмов неверно: если морфизм  : F
: F  G сюръективен, то отображения сечений
G сюръективен, то отображения сечений  (U): F(U)
(U): F(U)  G(U) могут не быть сюръективными. Однако можно утверждать что морфизм
G(U) могут не быть сюръективными. Однако можно утверждать что морфизм  сюръективен тогда и только тогда, когда отображения слоев
сюръективен тогда и только тогда, когда отображения слоев  p: Fp
p: Fp  Gp сюръективны для всех точек P. Более общим образом последовательность пучков и морфизмов точна тогда и только тогда, когда она точна послойно. Это указывает на локальную природу пучков.
Gp сюръективны для всех точек P. Более общим образом последовательность пучков и морфизмов точна тогда и только тогда, когда она точна послойно. Это указывает на локальную природу пучков.
Современная алгебраическая геометрия во многом опирается на теорию пучков. Одним из главных понятий этой теории является понятие схемы. В конце 1950-х годов Александр Гротендик дал определение схемы, обобщающее понятие алгебраического многообразия. Чтобы сформулировать понятие схемы, необходимо привести несклолько предварительных определений.
Локальное кольцо — это кольцо, которое относительно просто и позволяет описывать «локальное поведение» функций на алгебраическом многообразии или обычном многообразии.
Окольцованное пространство 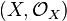 — это топологическое пространство
— это топологическое пространство 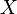 вместе с пучком коммутативных колец
вместе с пучком коммутативных колец 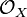 на нём. Этот пучок называется структурным пучком пространства
на нём. Этот пучок называется структурным пучком пространства 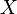 .
.
Локально окольцованное пространство — это окольцованное пространство, такое что слой пучка 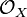 в любой точке — локальное кольцо.
в любой точке — локальное кольцо.
В топологии Зарисского замкнутыми множествами спектра кольца считаются множества всех простых идеалов, содержащих некоторое множество 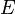 или, что то же самое, порождённый им идеал
или, что то же самое, порождённый им идеал 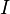 .
.
Если X — алгебраическое многообразие с топологией Зарисского (например, спектр некоторого кольца), то структуру локально окольцованного пространства на нём вводят следующим образом: 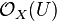 — множество рациональных функций, определённых на всём U. Такое окольцованное пространство называют аффинной схемой.
— множество рациональных функций, определённых на всём U. Такое окольцованное пространство называют аффинной схемой.
Общие схемы определяют как результат «склейки» нескольких аффинных схем.
Более подробно о пучках, их разновидностях, схемах и их использовании, а также связанных с ними понятиях можно прочитать в книгах [21] и [26].
Дата добавления: 2019-02-12; просмотров: 488; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
