Задачи для самостоятельной работы

⇐ ПредыдущаяСтр 25 из 26Следующая ⇒

1. Пусть Y 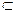Aⁿ – аффинное алгебраическое множество в аффинном пространстве Aⁿ и I(Y) – cоответствующий ему идеал. Факторкольцо A(Y)=A/I(Y) будем называть аффинным координатным кольцом множества Y. Пусть теперь Y – плоская кривая y=x² (т.е. Y есть множество нулей многочлена f=y-x²). Показать, что кольцо A(Y) изоморфно кольцу многочленов от одной переменной над основным полем k.

2. Рассмотрим морфизм φ: A¹ 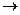A², заданный формулой t 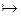(t², t³). Показать, что φ определяет отображение A¹ на кривую y²=x³, но не является изоморфизмом.

3. Для абелевой группы A и топологического пространства X определим постоянный предпучок на X, ассоциированный с A, как предпучок U 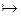A для всех открытых подмножеств U 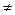Ø с тождественными отображениями ограничения. Показать, что постоянный пучок А, определенный выше, является пучком, ассоциированным с этим предпучком.

4. (a) Пусть F^¢ – подпучок пучка F. Показать, что естественное отображение пучка F в факторпучок F/ F^¢ сюръективно и его ядром является пучок F^¢. Таким образом, имеет место следующая точная последовательность 0®F^¢ ®F®F/F^¢ ®0.

(b) Обратно, если 0 ® F^¢® F ® F^¢¢® 0 – точная последовательность пучков, то показать, что F^¢ изоморфен подпучку пучка F, F^¢¢– факторпучку пучка F по этому подпучку.

5. Пусть φ: F 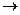G – морфизм пучков.

(а) Показать, что Im φ 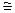F / Ker φ.

(b) Показать, что Coker φ 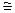G / Im φ.

Индивидуальные задания по вариантам (десять вариант, номер определяется по последней цифре зачетной книжки)

Задание 1.

0. Докажите, что относительно бинарной операции множество R не содержит нейтрального элемента. Является ли данная операция обратимой на множестве R.

1. Обладает ли множество N правым нейтральным элементом; левым нейтральным элементом; нейтральным элементом относительно бинарной операции, выполняемой по правилу а ◦ b = а^b ? Обратима ли данная операция на множестве N?

2. Докажите, что относительно бинарной операции, выполняемой по правилу 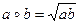, множество R⁺ не обладает нейтральным элементом. Обратима ли эта операция на множестве R⁺?

3. Покажите, что действие, выполняемое по правилу а◦b=а² + b², является коммутативной, но не ассоциативной бинарной операцией на множестве R.

4. Почему множество R не является полугруппой относительно действия, выполняемого по правилу а◦b = а² + b² для любых а, b Î R?

5. Докажите, что на множестве Q действие, выполняемое по правилу , является бинарной операцией, которая коммутативна, ассоциативна, но не обратима. Каким нейтральным элементом обладает алгебраическая система (Q, ◦)?

6. Докажите, что на множестве Z действие, выполняемое по правилу 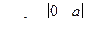, является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система (Z,◦) нейтральным элементом?

7. Докажите, что на множестве М матриц вида 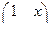, где х – любое действительное число, бинарная операция матричного умножения обратима.

8. Покажите, что множество {1, 0, -1} образует полугруппу относительно обычной операции умножения.

9. Докажите, что во множестве К, содержащем не менее двух элементов, на котором формулой а ◦ b = b задана бинарная операция, не существует нейтрального элемента.

Задание 2. Является ди данное отображение изоморфным отображением указанных алгебр.

0. а) ƒ: (Z, +) → (Z, +), ƒ(а) = а + 1

б) ƒ: (Q[ 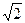], +) → (Q[ ], +), ƒ(а +b 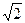) = а + b

1. а) ƒ: (Z, +) → (Z, +), ƒ(а) = 2а

б) ƒ: (Q[ 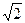], +) → (Q, +), ƒ(а +b 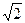) = а

2. а) ƒ: (Z, +) → (Z, +), ƒ(а) = -а

б) ƒ: (Q[ 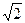], +) → (Q[ 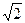], +), ƒ(а + b 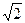) = а - b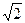

3. а) ƒ: (N, +) → (N, ∙), ƒ(а) = 2^а

б) ƒ: ( 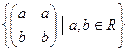, +) → (R, +), ƒ 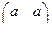= а + b

4. а) ƒ: (R⁺, ∙) → (R⁺, ∙), ƒ(а) = 1/а

б) ƒ: ( 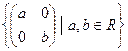, +) → (R, +), ƒ 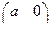= а

5. а) ƒ: (R⁺, ∙) → (R, ∙), ƒ(а) = 1/а

б) ƒ: ( 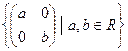, +) → (R, +), ƒ 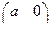= b

6. а) ƒ: (R⁺, ∙) → (R, +), ƒ(а) = ln а

б) ƒ: ( 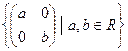, +) → (R, +), ƒ 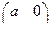= а + b

7. а) ƒ: (N, +) → (R, ∙ ), ƒ(а) = 1/2а

б) ƒ: ( 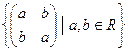, +) → (R, +), ƒ 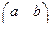= а - b

8. а) ƒ: (R, +) → (R⁺, ∙), ƒ(а) = 3^x

б) ƒ: ( 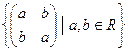, +) → (R, +), ƒ 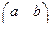= а + b

9. а) ƒ: (Z, +) → (2Z, ∙ ), ƒ(x) = x

б) ƒ: ( 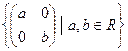, +) → (R, +), ƒ 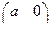= b

Задание 3.

0. Является ли группой множество чисел вида а + b 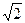относительно сложения, если а и в любые рациональные числа.

1. Является ли множество квадратных трехчленов вида А = {ах²+bх+с ‌ а, b, с Î R} группой относительно сложения?

2. Является ли множество (Z, ◦) группой, если а ◦ b = 2а + 3b?

3. Образуют ли группу положительные числа, если операция определна так а ◦ b = а² b²?

4. Является ли множество М целых чисел , кратных трем подгруппой аддитивной группы Z?

5. Докажите, что в аддитивной группе R² множество пар вида (а, 0) образует подгруппу.

6. Образует ли группу множество, состоящее из степеней данного действительного числа а, а ¹ 0, ± 1, с целыми показателями относительно умножения?

7. На множестве Q\{0} определено действие 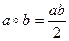. Докажите, что относительно указанного действия данное множество является группой.

8. Пусть а × а = е для любого элемента а мультипликативной группы G. Докажите, что группа G является абелевой.

9. Докажите, что если в группе <G₁, · > для любого а Î G а^-1 = а, то группа G – абелева.

Задание 4. Выясните, образует ли поле следующее множество относительно указанной операции.

0. Множество всех матриц вида 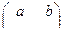, а, b Î Q относительно сложения и умножения матриц.

1. Множество всех матриц вида 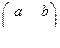, а, b Î Q относительно сложения и умножения матриц.

2. Множество всех матриц вида 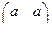, а Î R относительно сложения и умножения матриц.

3. Множество чисел вида а + b 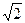с целыми а и b относительно сложения и умножения чисел.

4. Множество чисел вида а + b с целыми а и b относительно сложения и умножения чисел.

5. Множество пар (а, b) рациональных чисел относительно бинарных операций, заданных по следующим правилам:

(а, b) + (с,d) = (а+с, b+d)

(а, b) · (с,d) = (ас+2bd; аd+bс)

6. Множество упорядоченных пар (а, b) в котором сложение и умножение определены по следующим правилам:

(а,b) + (с,d) = (а+с, b+d)

(а,b) · (с,d) = (ас+5bd; аd+bс), где а и b - любые рациональные числа.

7. Множество упорядоченных пар (а, b) в котором сложение и умножение определены следующим образом:

(а,b) + (с,d) = (а+с, b+d)

(а,b) · (с,d) = (ас-bd; аd+bс), где а и b любые рациональные числа.

8. Множество L чисел вида а + b + с 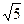, а, b Î Z относительно обычных операций сложения и умножения чисел.

9. Множество комплексных чисел вида а +bi с рациональными а и b относительно сложения и умножения.

Задание 5.

ЗАКЛЮЧЕНИЕ

Перед педагогическими университетами стоит проблема подготовки выпускников с качествами, адаптированными к потребностям общества.

Их подготовка осуществляется через обновленный образовательный процесс. В связи с этим возникает необходимость обеспечения студентов материалами, позволяющими не только организовать собственную учебную деятельность, но и отражающие развивающий потенциал математики.

Важность теории алгебраических структур определяется многочисленными ее приложениями не только внутри самой алгебры, но и в ряде разделов других математических дисциплин, информатики, физики, химии.

В связи с этим данное учебное пособие ориентируется на студентов педагогических вузов, изучающих теорию алгебраических структур, и представляет собой важнейший элемент совершенствования методического обеспечения математических дисциплин.

Не менее важна значимость учебного пособия в плане организации самостоятельной работы студентов, поскольку оно содержит весьма значительную по объему и по существу подборку заданий для самостоятельного решения.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Федеральный государственный образовательный стандарт высшего профессионального образования по направлению подготовки 050100 Педагогическое образование (квалификация (степень) «бакалавр») http://www.edu.ru/db-mon/mo/Data/d_09/prm788-1.pdf

2. Алгебра и теория чисел /Под ред. Н.Я.Виленкина. – М.: Просвещение, 1984. – 192с.

3. Александров П.С. Введение в теорию групп. – М.: Наука, 1980. – 143с.

4. Алфёров А.П., Зубов А.Ю., Кузьмин А.С., Черёмушкин А.В. Основы криптографии: Учебное пособие. – 3–е изд., испр. и доп. − М.: Гелиос АРВ, 2005.

5. Афанасьев В.В. Теория вероятностей – М.: Владос, 2007. − 350 с.

6. Варпаховский Ф.Л. и др. Алгебра: Группы, кольца, поля. Векторные и евклидовы пространства. Линейные отображения. М.: Просвещение, 1978. 144 с.

7. Варпаховский Ф.Л., Солодовников А.С. Алгебра. М.: Просвещение, 1981. 166 с.

8. Варпаховский Ф.Л., Солодовников А.С. Задачник-практикум по алгебре. Часть 1. М.: Просвещение, 1982. 79 с.

9. Вербiцький О.В. Вступ до криптологiï. – Львiв: ВНТЛ, 1998.

10. Вечтомов Е.М. Введение в полукольца. – Киров: ВятГПУ, 2000. – 44 с.

11. Вечтомов Е.М. Основные структуры классической математики. – Киров: ВятГПУ, 2007. – 252 с.

12. Винберг Э.Б. Курс алгебры. – М.:Факториал, 2002. – 544с.

13. Каргополов М.И., Мерзляков Ю.И. Основы теории групп. – Спб.: Издательство «Лань». 2009. – 288 с.

14. Кострикин А.И. Введение в алгебру. Основы алгебры. – М.: Физматлит, 1994. – 320 с.

15. Кузнецова И.В., Костиков А.Н., Самсонова С.А. Математика и информатика: учебное пособие с грифом УМО по направлениям пед. образования – Санкт-Петербург: Издательство РГПУ им. А.И. Герцена, 2006. – 154 с.

16. Куликов Л.Я. Алгебра и теория чисел. – М.: Высш. школа, 1979. – 559с.

17. Куликов Л.Я., Москаленко, Фомин А.А. Сборник задач по алгебре и теории чисел. – М.: Просвещение,1993. – 288 с.

18. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1971. – 432с.

19. Ленг С. Алгебра. – М.: Мир, 1968. – 564с.

20. Монахов В.С. Алгебра и теория чисел: учеб.пособие. В 2 ч. Ч.1/ В.С. Монахов, А.В. Бузланов. – Минск: Изд.центр БГУ.2007. – 264 с.

21. Оконек К., Шнейдер М., Шпиндлер Х. Векторные расслоения на комплексных проективных пространствах [Текст]. – М.: Мир, 1984. – 308 с.

22. Сборник задач по алгебре /Под ред. А.И. Кострикина. – М.: Физматлит, 2001. – 464с.

23. Серр Ж.П. Когерентные алгебраические пучки [Текст] // Расслоенные пространства и их приложения – М.: ИЛ, 1958. – С. 372-458.

24. Фаддеев Д.К. Лекции по алгебре. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 416 с.

25. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб: Издательство «Лань», 2001.

26. Хартсхорн Р. Алгебраическая геометрия [Текст]. – М.: Мир, 1981. – 597 с.

Дата добавления: 2019-02-12; просмотров: 469; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 17 18 19 20 21 22 23 242526 Следующая ⇒

Мы поможем в написании ваших работ!