Шнеперман Л.Б. Сборник задач по алгебре и теории чисел. – Мн.: Издательство «Дизайн ПРО», 2000. – 240с.
ПРИЛОЖЕНИЕ
ЗАДАНИЯ ЭЛЕКТИВНОГО КУРСА ПО ТЕМЕ «ОСНОВНЫЕ АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ»
(для учащихся средних школ)
1. Установить, какие арифметические действия определены:
а) во множестве нечетных чисел; б) во множестве четных чисел; в) во множестве чисел кратных 6.
2. Являются ли алгебраическими операции:
а) сложение на множестве {-1; 0; 1};
б) умножение на множестве всех целых чисел не делящихся на 5; не делящихся на 15?
3. Является ли алгебраической операцией на множестве М ={1; 2; 3} отображение, заданное на рисунках 1, 2, 3 при помощи стрелок?

Рис. 1. Рис. 2. Рис. 3.

4. Найдите все конечные подмножества Z, на которых:
а) умножение является алгебраической операцией;
б) сложение является алгебраической операцией.
5. Найдите наименьшее подмножество Z, содержащее число 2 на котором вычитание было бы алгебраической операцией.
6. Найдите два подмножества Z, на которых деление является алгебраической операцией.
7.  Пример часовой арифметики – арифметики вычетов по данному натуральному модулю. Учащимся предлагается начертить циферблат с пятью делениями, которые являются элементами множества {0; 1; 2; 3; 4}. Примем соглашение, что 1+2 означает следующее: стрелка устанавливается на 0, затем она перемещается на одно деление, а потом ещё на два деления. Составить таблицу операции «сложение» в созданной математической системе.
Пример часовой арифметики – арифметики вычетов по данному натуральному модулю. Учащимся предлагается начертить циферблат с пятью делениями, которые являются элементами множества {0; 1; 2; 3; 4}. Примем соглашение, что 1+2 означает следующее: стрелка устанавливается на 0, затем она перемещается на одно деление, а потом ещё на два деления. Составить таблицу операции «сложение» в созданной математической системе.
8. Сейчас 8 часов утра. Какой время покажут стрелки через 60 часов?
9. Восьмое марта в этом году пришелся на понедельник. В какой день недели этот праздник будет в следующем году?
10. Покажите, что во множестве поворотов квадрата вокруг центра, совмещающих его с самим собой, сумма двух поворотов есть алгебраическая операция. Составьте таблицу сложения.
11. Какие из приведённых ниже операций будут коммутативными, ассоциативными на множестве N: а) a◦b=c, где c=(a; b); б) a◦b=c, где c=[a; b]; в) a◦b=ab; г) a◦b=a+3b.
12.  На множестве действительных чисел определены две алгебраические операции * и ◦ следующим образом: a*b=(a+b)/2; a◦b= , a, b³0.
На множестве действительных чисел определены две алгебраические операции * и ◦ следующим образом: a*b=(a+b)/2; a◦b= , a, b³0.
Являются ли эти операции ассоциативными, коммутативными?
13. Привести примеры операций на множестве R, которые:
а) ассоциативные, но не коммутативные;
б) коммутативные, но не ассоциативные.
14. Доказать, что алгебраическая операция *, определённая во множестве целых чисел при помощи формулы a*b=a+b-2; a, bÎZ является коммутативной и ассоциативной.
15. Как по таблице Кэли, определить, является ли операция коммутативной? Является ли операция из упражнения 7 коммутативной?
16. Выясните, какие из множеств упражнение 11,12 обладают нейтральными элементами.
17. Найдите нейтральный элемент алгебраической операции, определённой в упражнении 7. Как с помощью таблицы Кэли решить вопрос о наличии нейтрального элемента?
18. Пусть А – множество всех подмножеств {1; 2; 3; 4; 5}. Существует ли и каков именно нейтральный элемент в (A,*), если:
а) а*b= a I b; б) a*b=a U b?
19. Найти нейтральный элемент алгебраической операции *, определённой в упражнении 14.
20. Доказать, что во множестве R, с алгебраической операцией *, определённой формулой a*b=(a+b)/2 нет нейтрального элемента.
21. Доказать следующую теорему:
«Если алгебраическая система (G,*) обладает нейтральным элементом n, то он единственный».
22. Доказать, что если n/ – левый нейтральный элемент, n// – правый нейтральный элемент в G, то n/=n//.
23. Рассмотрим алгебраическую систему (Z,*), где операция * определена следующим образом: 0*0=0 и для a, b¹ 0

Покажите, что данная операция не является ассоциативной. Найти нейтральный и симметричные элементы.
24. Докажите, что если некоторый элемент алгебраической системы имеет более одного симметричного, то эта система не обладает свойством ассоциативности.
25. Есть ли обратимые элементы в алгебраической системе (N, ×); (Q, ×).
26. Все ли элементы обратимы в алгебраической системе (Q,*), где a*b=a+b+ab?
27. Выяснить какими свойствами (коммутативность, ассоциативность, нейтральный элемент, для каждого ли элемента есть симметричный ему элемент) обладает операция:
 а) сложение на множестве чисел вида {a+b ça, bÎZ};
а) сложение на множестве чисел вида {a+b ça, bÎZ};
б) сложение по модулю 5 на множестве чисел вида {0; 1; 2; 3; 4};
в) сложение на множестве четных чисел;
г) x◦y=x2+y2, где x, yÎR;

д) a*b=
28. Образует ли группу множество
а) рациональных чисел; б) четных чисел;
 в) чисел вида a+b , где a, bÎZ; г) {-1; 0; 1} относительно сложения;
в) чисел вида a+b , где a, bÎZ; г) {-1; 0; 1} относительно сложения;
д) положительных рациональных чисел; е) {-1; 1};
ж) чисел вида 2m, где mÎZ относительно умножения.
29. Укажите наименьшее множество чисел, содержащее число 2 и являющееся:
а) группой относительно сложения;
б) группой относительно умножения.
30. Покажите, что множество всех рациональных чисел, кроме 1, является группой относительно операции *: a*b=2(a-1)(b-1)+1.
31. Является ли группой множество {-1; 0; 1} относительно умножения.
32. Доказать, что множество М={10x çxÎZ} относительно операции умножения является группой.
33. Доказать, что уравнение a+x=b разрешимо во множестве Z.
34. В группе (Z7,+) решить уравнение 5+x=3
35. Доказать, что в группе имеют место равенства:
а) a - m =( am )-1; б) ap * aq = ap + q = aq * ap ; в) ( ap ) q = apq ; г) Если группа абелева, то ( ab ) n = anbn .
36. Элемент G группоида называется идемпотентным элементом, если g*g=g. Докажите, что единственным идемпотентным элементом группы является единица.
37. Сформулируйте свойства групп на аддитивном языке.
38. Определить тип структуры следующих алгебраических систем:
а) (N,+); (N, ×); (N,*), где a*b=2a+b; (N, ◦), где a◦b=a, a, bÎN;
б) (Z,+); (Z,-); в) (Q,+); (R,+); (R*, ×);
г) ({1},×); ({0},+); ({0; 1},×),({-1;1},×);
д) (R2,+), где R2={(a; b) /a, bÎZ} (a; b)+(c; d)=(a+c; b+d).
39. (Q+ ,×) является подгруппой группы (Q0, ×), группа (Q0,×) – подгруппа (R0, ×).
40. Показать, что {е} есть подгруппа группы (G, ×).
41. Будут ли подгруппой группы (Q,+) множества 3Z, 4Z, 5Z?
42. В группе Z5 ={0; 1; 2; 3; 4} относительно операции сложения по модулю 5 указать какую–нибудь подгруппу второго порядка и подгруппу третьего порядка.
43. Доказать, что пересечение двух подгрупп есть подгруппа.
44. Рассмотрим множество векторов на плоскости, исходящие из точки O, которые являются группой относительно сложения. Являются ли подгруппами этой группы следующие множества:
а) нулевой вектор;
б) множество векторов, концы которых находятся во второй четверти;
в) множество векторов, лежащих на прямой, исходящей из начала координат.
45. Пусть D3 - множество всех самосовмещений равностороннего треугольника. Показать, что это множество состоит только из шести элементов: D3={E, R0120°, R0240°, Sl1 , Sl2 , Sl3 }.
46. Верно ли утверждение: композиция любых двух перемещений из D3 есть снова перемещение из D3?
47. Какой элемент в этом множестве является нейтральным? Для каждого перемещения из D3 найдите обратное ему перемещение.
48. Выполняется ли ассоциативный закон для композиции самосовмещений равностороннего треугольника?
49. Вычислите группы симметрий следующих фигур:
а) двух взаимно перпендикулярных прямых; б) прямоугольника;
в) равнобедренной трапеции; г) параболы; д) гиперболы.
50. Относятся ли следующие фигуры к одному классу симметрии:

51. Какие из следующих отображений группы (Z, +) в группу (2Z, +) являются изоморфизмами: а) f(Z)=2Z+2; б) f(Z)=-2Z; в) f(Z)=4Z?
52. Установить изоморфизм между группами (R+,×) и (R,+). Следующий пример даёт учащимся понятие об автоморфизмах групп.
53. Покажите, что отображение f(x)= 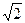 и g(x)=1/x задаёт изоморфизм группы (R+, ×) с самой собой.
и g(x)=1/x задаёт изоморфизм группы (R+, ×) с самой собой.
54. Является ли отображение f(a+b 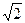 )=a-b
)=a-b 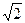
 автоморфизмом группы (M, +), где M={a+b
автоморфизмом группы (M, +), где M={a+b 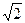 ç a, bÎZ}.
ç a, bÎZ}.
55. Установить, изоморфны ли группы (R*, ×) и {(a; b)ça, bÎZ, a¹0, b¹0),×}, где (a; b) ×(c; d)=(a×c; b×d) для любых пар (a; b), (c; d).
56. Изоморфны ли группы:
а) (M1,+) и (M2,+), где M1={2m ç mÎZ}, M2={7k, kÎZ};
б) (K1,+) и (K2,+), где K1={a+b 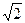 ça, bÎZ} и K2={a+b
ça, bÎZ} и K2={a+b  ça, bÎZ};
ça, bÎZ};
57. Все группы вида ({a+b  ç a, bÎZ},+) изоморфны между собой, но группы ({a+b
ç a, bÎZ},+) изоморфны между собой, но группы ({a+b  ça, bÎZ},×) не изоморфны. Почему?
ça, bÎZ},×) не изоморфны. Почему?
58. Какие из следующих отображений являются изоморфными:
а) f1: (R0, ×)®(R+, ×), где f1(x)=½x½; б) f2: (R0, ×)®(R0,×), где f2(x)=2/x;
в) f4: (2Z,+)®(Z,+), где f4(x)=x.
59. Будет ли кольцом множество:а) четных; б) нечетных целых чисел относительно арифметических действий сложения и умножения.
60. Образует ли кольцо: а) множество натуральных чисел;
б) множество всех целых чисел, кратных числу 3;
61. Установить, что множество всех целых чисел, кратных натуральному числу n, относительно арифметических действий сложения и умножения является кольцом.
 62. Доказать, что множество чисел вида a+b , где a, bÎZ образует относительно арифметических действий сложения и умножения кольцо.
62. Доказать, что множество чисел вида a+b , где a, bÎZ образует относительно арифметических действий сложения и умножения кольцо.
63. Образует ли кольцо множество всевозможных пар {(a; b) êa, bÎZ}, в котором операции сложения и умножения заданы следующим образом:
(a; b)+(c; d)=(a+c; b+d); (a; b)× (c; d)=(ac; bd).
64. Привести примеры колец без делителей нуля.
65. Пусть K={0; 1; 2; 3}. Операции Å и ¤ определим правилом:
aÅb={остаток от деления a+b на 4}, a¤b={остаток от деления a•b на 4}. Докажите, что K является кольцом относительно указанных операций и что в нём есть делители нуля.
66. Привести примеры подколец кольца (R,+, ×).
67. Для каждого из следующих множеств определите, является ли оно полем:
а) множество четных чисел; б) множество вычетов по модулю 3; в) множество чисел вида {aÖ2 êaÎQ}.
68. Доказать, что всякое поле не содержит делителей нуля.
69. Покажите, что кольцо A={a0; a1}, где a0 - любое четное число, a1 - нечетное число, является полем.
70. Будет ли кольцо (Z,+,×) изоморфно кольцу ({2z êzÎZ},+,×).
71. Могут ли быть изоморфными поле рациональных и поле действительных чисел?
72. Можно ли кольцо (Q,+,×) отобразить на кольцо ({0},+,×)?
Дата добавления: 2019-02-12; просмотров: 616; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
