Задачи для самостоятельной работы
1. Доказать, что множество матиц размерности m на n над полем P с операцией сложения является абелевой группой.
2. Пусть A =  Выясните, является ли абелевой группой:
Выясните, является ли абелевой группой:
а) А с операцией сложения, б) А с операцией умножения.
3.Найти произведение матриц А и В, если
а)  б)
б) 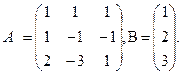
4. Найти f ( A ), если f ( x ) = 2 x  + 3 x + 2 E , A =
+ 3 x + 2 E , A = 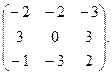
Метод Гаусса решения систем линейных уравнений
Системой из m линейных уравнений с n неизвестными называется система вида:
( S ) 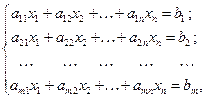
где  – коэффициенты системы,
– коэффициенты системы,  – свободные члены системы,
– свободные члены системы,  – переменные системы; все они принадлежат некоторому полю P.
– переменные системы; все они принадлежат некоторому полю P.
Говорят, что n-ка (  удовлетворяет системе ( S ), если при замене
удовлетворяет системе ( S ), если при замене 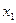 на
на  ,
,  на
на  ,
,  на
на  , система ( S ) превращается в систему верных равенств.
, система ( S ) превращается в систему верных равенств.
Решением системы ( S ) называется любая n-ка 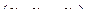 , удовлетворяющая системе ( S ).
, удовлетворяющая системе ( S ).
Если система линейных уравнений имеет хотя бы одно решение, она называется совместной. Система, не имеющая решений, называется несовместной.
Две системы с n переменными называются равносильными над полем P, если их множества решений над этим полем совпадают.
Если b1 = b2 = ... = bm = 0, то система называется однородной, и неоднородной в противном случае.
Система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если решений более одного.
Коэффициенты при неизвестных aij (i = 1, 2, …, m; j = 1, 2, …, n) образуют матрицу 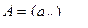 , которая называется матрицей коэффициентов системы.
, которая называется матрицей коэффициентов системы.
При решении систем важными являются два вида уравнений:
1) 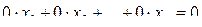 , решением этого уравнения является любая n-ка (
, решением этого уравнения является любая n-ка (  ;
;
2) 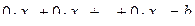 , где b
, где b 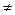 0, такое уравнение и любая система, содержащая такое уравнение, не имеет решений.
0, такое уравнение и любая система, содержащая такое уравнение, не имеет решений.
Существует ряд преобразований над системой ( S ), которые называют элементарными. К ним относятся следующие преобразования:
1) умножение любого уравнения системы ( S ) на любое 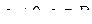 ;
;
2) перемена уравнений местами;
3) прибавление к одному уравнению системы ( S ) любого другого уравнения, умноженного на любое 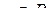 ;
;
4) вычеркивание из системы ( S ) уравнения вида 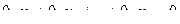 .
.
Важность элементарных преобразований объясняется справедливостью следующей теоремы.
Теорема 2.1. При элементарных преобразованиях в системе линейных уравнений система переходит в равносильную ей систему.
На элементарных преобразованиях основан очень удобный в практическом отношении способ решения системы ( S ) – метод Гаусса.
Система уравнений вида:
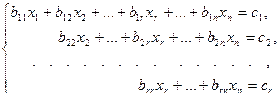
где 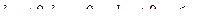 называется ступенчатой (трапециевидной) системой уравнений.
называется ступенчатой (трапециевидной) системой уравнений.
В методе Гаусса систему линейных уравнений приводят элементарными преобразованиями к равносильной ей ступенчатой системе, у которой находят решения. При этом все элементарные преобразования в системе осуществляют с помощью матриц.
Рассмотрим систему линейных уравнений ( S ). К матрице коэффициентов системы 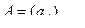 допишем справа столбециз свободных членов системы b1, b2, ...,bm, получим новую матрицу, которая называется расширенной матрицей системы и обозначается:
допишем справа столбециз свободных членов системы b1, b2, ...,bm, получим новую матрицу, которая называется расширенной матрицей системы и обозначается: 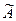 , т.е.
, т.е.
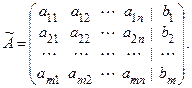
Элементарным преобразованиям в системе уравнений соответствуют аналогичные преобразования со строками расширенной матрицы. Метод Гаусса состоит из двух частей – прямого и обратного хода. Идея прямого хода метода – с помощью элементарных преобразований привести расширенную матрицу к ступенчатому виду.
Прямой ход метода Гаусса
Шаг 1. Если а11 = 0, то с помощью перемены строк местами добиваемся, чтобы на место этого элемента попал ненулевой элемент. Если в системе при первой переменной все коэффициенты нулевые, то можно произвести замену переменных местами, что в дальнейшем нужно учитывать. Если в матрице коэффициентов нет ненулевых элементов, то все зависит от того, есть ли в системе ненулевые свободные члены. Если таковых нет, то решением такой системы является любая n-ка (  ; если же есть, то это означает, что в системе присутствует уравнение
; если же есть, то это означает, что в системе присутствует уравнение 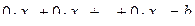 , где b
, где b 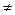 0, поэтому система не имеет решений.
0, поэтому система не имеет решений.
Пусть в матрице 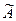 элемент
элемент 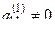 (верхний индекс указывает на номер шага):
(верхний индекс указывает на номер шага):
 .
.
Так как 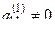 и
и 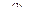 P, то в поле P имеется обратный для этого элемента элемент
P, то в поле P имеется обратный для этого элемента элемент 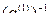 =
= 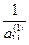 . Умножим элемент первой строки на число
. Умножим элемент первой строки на число 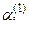 и прибавим к соответствующим элементам i-й строки (i = 2, 3, ...., m). Числа
и прибавим к соответствующим элементам i-й строки (i = 2, 3, ...., m). Числа 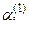 подберем так, чтобы первые элементы в строках обратились в 0, т.е.
подберем так, чтобы первые элементы в строках обратились в 0, т.е. 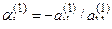 . В результате получим матрицу, в которой в первом столбце под главной диагональю все элементы равны 0. Обозначим полученную матрицу
. В результате получим матрицу, в которой в первом столбце под главной диагональю все элементы равны 0. Обозначим полученную матрицу  :
:
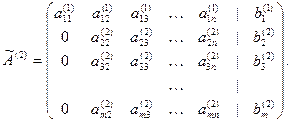
Если после преобразований в системе появилось уравнение 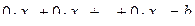 , где b
, где b 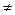 0, то на этомостанавливаем работу алгоритма, делая вывод о несовместности исходной системы.
0, то на этомостанавливаем работу алгоритма, делая вывод о несовместности исходной системы.
Если же ли в результате преобразований появились уравнения вида 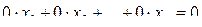 , то вычеркиваем их и переходим к следующему шагу.
, то вычеркиваем их и переходим к следующему шагу.
Шаг 2. Если 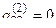 , то, как и в первом шаге, добиваемся того, чтобы на место этого элемента попал ненулевой элемент матрицы. Пусть
, то, как и в первом шаге, добиваемся того, чтобы на место этого элемента попал ненулевой элемент матрицы. Пусть  , умножим элементы второй строки на число
, умножим элементы второй строки на число 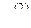 и прибавим к соответствующим элементам i-й строки (i = 3, 4, ..., m). Числа
и прибавим к соответствующим элементам i-й строки (i = 3, 4, ..., m). Числа 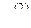 подберем так, чтобы вторые элементы в строках обратились в нули, т.е.
подберем так, чтобы вторые элементы в строках обратились в нули, т.е. 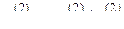 . В результате получим матрицу, в которой во втором столбце под главной диагональю все элементы равны нулю:
. В результате получим матрицу, в которой во втором столбце под главной диагональю все элементы равны нулю:
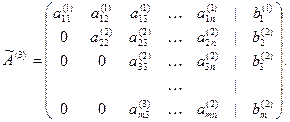
Будем выполнять указанные преобразования до тех пор, пока матрица системы А не примет ступенчатый вид или же в системе не встретится уравнение  , где b
, где b 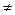 0. Если такого уравнения не встретится, то на некотором шаге с номером r будет получена матрица, которой соответствует система уравнений, равносильная исходной, вида:
0. Если такого уравнения не встретится, то на некотором шаге с номером r будет получена матрица, которой соответствует система уравнений, равносильная исходной, вида:
(S’) 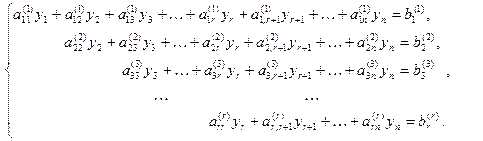
Здесь неизвестные обозначены: y1, …, yn, потому что, возможно, в процессе работы алгоритма пришлось поменять местами столбцы матрицы коэффициентов, в связи с чем естественный порядок переменных х1, х2 …, хn нарушился. Например, если в расширенной матрице поменяли местами столбцы с номерами k и р, то в системе на месте слагаемых с номерами неизвестных k будут слагаемые с номерами неизвестных р и наоборот, т.е. уk = xp и уp = хk. На этом прямой ход метода Гаусса заканчивается.
Обратный ход метода Гаусса
Назовем неизвестные у1, y2, ..., уr базисными, а уr+1, уr+2 ,…, уn свободными.
Шаг 1. Из последнего уравнения системы (S’) выразим переменную уr через свободные переменные:
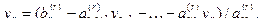
Шаг 2. Подставляем найденный уr в предпоследнее уравнение и находим yr-1:

. . .
Шаг r. Подставляя найденные уr, …, у2 в первое уравнение, находим у1:
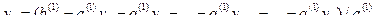
В результате, получаем решение системы ( S ), в котором базисные переменные выражены через свободные переменные.
Теорема 2.2. Любая совместная система ( S ) методом Гаусса приводится к равносильной ей ступенчатой системе. Пусть полученная ступенчатая система содержит r уравнений. Если r = n, то система ( S ) имеет единственное решение; если r <  n, то система ( S ) имеет более одного решения. Если система ( S ) несовместна, то в процессе решения встретится уравнение вида:
n, то система ( S ) имеет более одного решения. Если система ( S ) несовместна, то в процессе решения встретится уравнение вида: 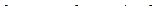 .
.
Замечание. Если в совместной системе линейной уравнений при приведении расширенной матрицы получили r <  n, то система ( S ) имеет бесконечно много решений в случае, если система рассматривается над полем с бесконечным числом элементов.
n, то система ( S ) имеет бесконечно много решений в случае, если система рассматривается над полем с бесконечным числом элементов.
Пример 1. Решим методом Гаусса систему уравнений над полем действительных чисел:
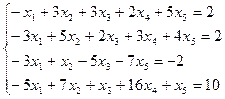 .
.
Решение.
Данной системе соответствует расширенная матрица:
 =
= 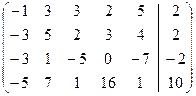 .
.
Приводим матрицу  к ступенчатому виду. Проведем ряд элементарных преобразований, чтобы в первом столбце все элементы, кроме первого, стали равны 0. Получим:
к ступенчатому виду. Проведем ряд элементарных преобразований, чтобы в первом столбце все элементы, кроме первого, стали равны 0. Получим:
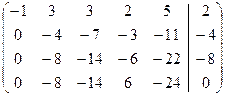
Первую строку оставим без изменений
Ко второй прибавим первую, умноженную на -3
К третьей прибавим первую, умноженную на -3
К четвертой прибавим первую, умноженную на -5
Проведем ряд элементарных преобразований, чтобы во втором столбце все элементы, стоящие под главной диагональю, стали равны 0. Получим:

Первую и вторую строку оставим без изменений
К третьей прибавим вторую, умноженную на -2
К четвертой прибавим вторую, умноженную на -2
Третьей строке матрицы соответствует уравнение вида 0=0, поэтому эту строку можно вычеркнуть, четвертую строку умножим на 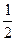 . Получим матрицу:
. Получим матрицу: 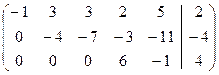 . Матрица еще не имеет ступенчатый вид, так как в третьем столбце полученной матрицы на главной диагонали стоит 0. Поэтому произведем перестановку третьего и пятого столбца (это соответствует перестановке переменных x3 и x5 в системе):
. Матрица еще не имеет ступенчатый вид, так как в третьем столбце полученной матрицы на главной диагонали стоит 0. Поэтому произведем перестановку третьего и пятого столбца (это соответствует перестановке переменных x3 и x5 в системе): 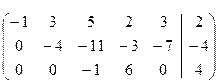 .
.
Система приведена к равносильной системе ступенчатого вида:

 .
.
Решений будет бесконечно много. Перемененные 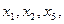 стоящие на главной диагонали, принимаем за главные переменные; переменные, стоящие правее (в нашем случае x4 и x3), считаем свободными переменными. Они могут принимать любые значения из поля R, поэтому система и будет иметь бесконечно много решений. Полагаем:
стоящие на главной диагонали, принимаем за главные переменные; переменные, стоящие правее (в нашем случае x4 и x3), считаем свободными переменными. Они могут принимать любые значения из поля R, поэтому система и будет иметь бесконечно много решений. Полагаем: 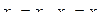 Из нижнего уравнения находим
Из нижнего уравнения находим 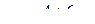 Поднимаясь постепенно в последней системе, получим:
Поднимаясь постепенно в последней системе, получим:

 .
.
На этом процесс решения исходной системы закончен. Получены выражения для неизвестных 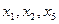 через
через  и
и  ; последние играют роль свободных переменных. Полагая например,
; последние играют роль свободных переменных. Полагая например, 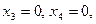 получим частное решение:
получим частное решение: 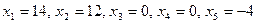 .
.
Пример 2. Решим систему уравнений над полем действительных чисел:
 .
.
Решение. Выпишем матрицу, соответствующую данной системе:
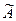 =
= 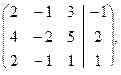 приводим её к ступенчатому виду.
приводим её к ступенчатому виду.
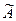 ~
~ 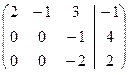 ~
~ 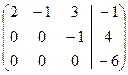 .
.
(Символом ~ обозначают переход от матрицы к матрице, которой соответствует система уравнений, равносильная исходной). 
Последней строке соответствует уравнение  , которому не удовлетворяют никакие значения переменных. Следовательно, данная система несовместна.
, которому не удовлетворяют никакие значения переменных. Следовательно, данная система несовместна.
Пример 3. Решим систему уравнений над полем действительных чисел:
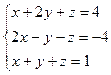 .
.
Решение.
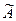 =
=  ~
~  ~
~ 
 .
.
Последней матрице соответствует система: 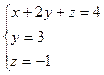 , то есть данная система уравнений имеет единственное решение:
, то есть данная система уравнений имеет единственное решение:  .
.
Пример 4. Исследуйте систему уравнений: 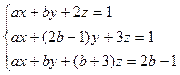
при всевозможных значениях параметров  и
и 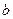 .
.
Решение.
Исследовать систему уравнений значит установить, при каких значениях параметров  и
и 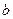 система совместна, и в каких случаях она несовместна, а также найти ее решения в случае совместности.
система совместна, и в каких случаях она несовместна, а также найти ее решения в случае совместности.
Считая параметры  и
и 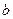 числами, приводим систему к ступенчатому виду:
числами, приводим систему к ступенчатому виду:
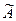 =
= 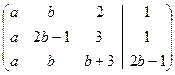 ~
~ 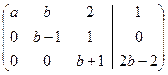 .
.
Исходная система равносильна системе:
 .
.
Сразу установим, когда система совместна.
1) Полученная система будет иметь единственное решение, если все коэффициенты в полученной ступенчатой системе не равны нулю, т.е. если а 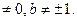 В этом случае решение будет следующим:
В этом случае решение будет следующим:
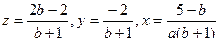
Далее рассмотрим случаи, когда  =0, или
=0, или 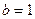 или
или  .
.
2)  , последнее уравнение в системе имеет вид: 0=-4, что означает, что система несовместна.
, последнее уравнение в системе имеет вид: 0=-4, что означает, что система несовместна.
3) 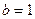 , система примет вид :
, система примет вид :  .
.
Из уравнения 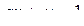 делаем вывод, что одна из переменных, например
делаем вывод, что одна из переменных, например 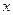 , будет свободной,
, будет свободной,  . Следовательно, при
. Следовательно, при 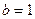 система имеет бесконечно много решений:
система имеет бесконечно много решений:  .
.
4) 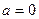 , получаем :
, получаем : 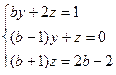 .
.
Так как случаи, когда 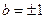 рассмотрены, то будем считать, что
рассмотрены, то будем считать, что 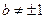 . Из третьего и второго уравнения находим:
. Из третьего и второго уравнения находим: 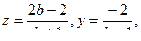 подставим их в первое уравнение, получим:
подставим их в первое уравнение, получим: 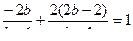 или
или 
Итак, если  , то система совместна только при
, то система совместна только при  , и в этом случае
, и в этом случае 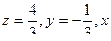 - любое.
- любое.
Ответ:
1) если  то
то  , т.е. система имеет единственное решение;
, т.е. система имеет единственное решение;
2) если 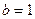 , то система имеет бесконечно много решений:
, то система имеет бесконечно много решений: 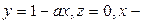 любое.
любое.
3) Если  , то система имеет бесконечно много решений: х-любое,
, то система имеет бесконечно много решений: х-любое,  .
.
В остальных случаях система несовместна.
Дата добавления: 2019-02-12; просмотров: 212; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
