Задачи для самостоятельной работы
1. Найти общее решение и одно частное решение системы линейных уравнений методом Гаусса:
а) 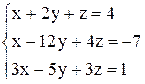 , в)
, в)  ,
,
б) 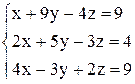 , г)
, г)  .
.
2. Найти решение однородной системы линейных уравнений:
а) 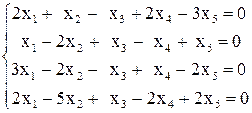 , в)
, в) 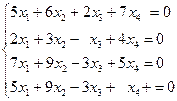 ,
,
б) 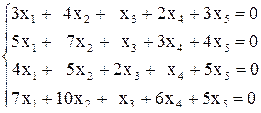 , г)
, г) 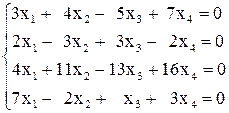 .
.
3. Исследовать и решить систему уравнений. Выполнить проверку общего решения.
а) 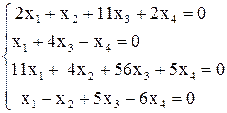 , в)
, в) 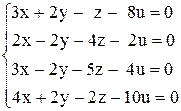 ,
,
б) 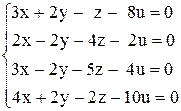 , г)
, г) 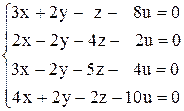 .
.
Применение метода Гаусса в линейной алгебре
Ранее, в параграфе 8 главы 2 были даны определения линейно зависимой, линейно независимой систем векторов, ранга системы векторов, базиса системы векторов и векторного пространства. Определить, линейно зависима система векторов или нет, выразить один вектор через другие можно, решив систему линейных уравнений методом Гаусса.
Пример 1. Выяснить, будет ли линейно зависимой система векторов: 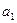 =(1,2,3,0),
=(1,2,3,0),  = (-1,2,3,0),
= (-1,2,3,0),  =(2,5,-2,3),
=(2,5,-2,3),  =(4,12,2,1).
=(4,12,2,1).
Решение. Используем определение. Из векторов составим линейную комбинацию с произвольными коэффициентами  , приравняем её к нулевому вектору, получим уравнение:
, приравняем её к нулевому вектору, получим уравнение: 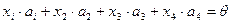 . Далее задача сводится к тому, чтобы выяснить, будет ли составленное уравнение иметь хотя бы одно ненулевое решение.
. Далее задача сводится к тому, чтобы выяснить, будет ли составленное уравнение иметь хотя бы одно ненулевое решение.
Поскольку равенство векторов означает равенство соответствующих координат, то получаем следующие равенства, которые рассматриваем как систему линейных однородных уравнений:
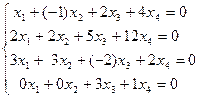 .
.
Решая её методом Гаусса, получаем, что она имеет единственное решение (0,0,0,0). Следовательно, система  линейно независима.
линейно независима.
|
|
|
Пример 2. Выяснить, можно ли вектор 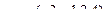 линейно выразить через систему
линейно выразить через систему  ,
, 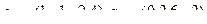 .
.
Решение: Допустим, что вектор  линейно выражается через систему векторов
линейно выражается через систему векторов 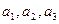 . Это означает, что можно составить следующую линейную комбинацию:
. Это означает, что можно составить следующую линейную комбинацию:  . Проверим, существуют ли действительно такие коэффициенты
. Проверим, существуют ли действительно такие коэффициенты  . Перейдем к равенству одноименных координат, получим следующую систему линейных уравнений:
. Перейдем к равенству одноименных координат, получим следующую систему линейных уравнений: 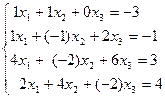 .
.
Задача свелась к тому, чтобы проверить, совместна ли полученная система. Решая её методом Гаусса, получаем, что она несовместна. Значит, вектор a  нельзя выразить через указанную систему векторов.
нельзя выразить через указанную систему векторов.
Пример 3. Для системы векторов 
 найти базис и ранг; через найденный базис выразить все остальные векторы системы.
найти базис и ранг; через найденный базис выразить все остальные векторы системы.
Решение. Для нахождения ранга системы векторов составляем из координат матрицу, подвергаем её элементарным преобразованиям для приведения к ступенчатому виду (ранг системы векторов при этом сохраняется). Справа от каждой строки (вектора) пишем её выражение через  .
.
A= 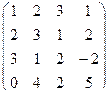
 ~
~ 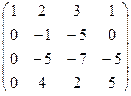
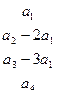 ~
~ 
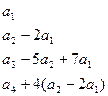 ~
~ 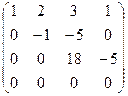
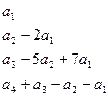 .
.
Выводы:
1) ранг системы векторов равен 3, так как в ступенчатой системе три вектора;
2) базис состоит из трех векторов; в качестве базиса взять удобнее те векторы, которые порождают ступенчатую систему векторов - 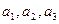
|
|
|
3) из последней строки матрицы найдем вектор  , не входящий в базис:
, не входящий в базис:  , поэтому
, поэтому  .
.
Дата добавления: 2019-02-12; просмотров: 195; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
