Производные и дифференциалы высших порядков.
Производные и дифференциалы высших порядков.
Пусть функция f ( x )- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
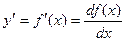
Если найти производную функции f ¢ ( x ), получим вторую производную функции f ( x ).

т.е. y ¢¢ = ( y ¢ ) ¢ или  .
.
Этот процесс можно продолжить и далее, находя производные степени n .
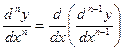 .
.
Общие правила нахождения высших производных.
Если функции u = f ( x ) и v = g ( x ) дифференцируемы, то
1) (С u)(n) = Cu(n);
2) (u ± v)(n) = u(n) ± v(n);
3) 
 .
.
Это выражение называется формулой Лейбница.
Также по формуле dny = f ( n ) ( x ) dxn может быть найден дифференциал n - го порядка.
Основные теоремы дифференциального исчисления: Ролля (с доказательством), Коши (без доказательства), Лагранжа (с доказательством).
Теорема Ролля
Если функция f ( x ) непрерывна на отрезке [ a , b ], дифференцируема на интервале (а, b ) и значения функции на концах отрезка равны f ( a ) = f ( b ), то на интервале (а, b ) существует точка e , a < e < b , в которой производная функция f ( x ) равная нулю,
f ¢ ( e ) = 0.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале ( a , b ) существует точка e такая, что в соответствующей точке кривой y = f ( x ) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
|
|
|
Доказательство. По свойству функций, непрерывных на отрезке функция f ( x ) на отрезке [ a , b ] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m .
Пусть M = m . Тогда функция f ( x ) на отрезке [ a , b ] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.
Пусть М = m . Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [ a , b ]. Обозначим e , a < e < b точку, в которой f ( e ) = M . Так как М- наибольшее значение функции, то для любого D х ( будем считать, что точка e + D х находится внутри рассматриваемого интервала) верно неравенство:
D f ( e ) = f ( e + D x ) – f ( e ) £ 0
При этом 
Но так как по условию производная в точке e существует, то существует и предел  .
.
Т.к.  и
и  , то можно сделать вывод:
, то можно сделать вывод:

Теорема доказана.
Теорема Ролля имеет несколько следствий:
1) Если функция f ( x ) на отрезке [ a , b ] удовлетворяет теореме Ролля, причем
f ( a ) = f ( b ) = 0, то существует по крайней мере одна точка e , a < e < b , такая, что f ¢ ( e ) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
|
|
|
Если на рассматриваемом интервале (а, b ) функция f ( x ) имеет производную ( n -1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная ( n – 1) – го порядка равна нулю.
Теорема Коши.
Если функции f ( x ) и g ( x ) непрерывны на отрезке [ a , b ] и дифференцируемы на интервале ( a , b ) и g ¢ ( x ) ¹ 0 на интервале ( a , b ), то существует по крайней мере одна точка e , a < e < b , такая, что
 .
.
Дата добавления: 2019-02-12; просмотров: 192; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
