При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций непрерывных в точке.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций 
– есть непрерывная функция при условии, что g ( x ) не равна нулю в точке х0.
Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f ( x ), v = g ( x ) – непрерывные функции в точке х = х0, то функция v = g ( f ( x )) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f ( x ) = C , C = const – непрерывная функция на всей области определения.
2) Рациональная функция 
непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
Тригонометрические функции sin и cos непрерывны на своей области определения.
Докажем свойство 3 для функции y = sinx .
Запишем приращение функции D y = sin ( x + D x ) – sinx , или после преобразования:
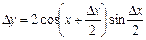
Действительно, имеется предел произведения двух функций 
и 
. При этом функция косинус – ограниченная функция при D х ® 0 
, а т.к.
предел функции синус 
, то она является бесконечно малой при D х ® 0.
Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция D у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
|
|
|
Свойства функций непрерывных на отрезке (теоремы Вейерштрасса, Коши, о промежуточных значениях) и их геометрических смысл.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [ a , b ] выполняется условие – M £ f ( x ) £ M .
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [ a , b ] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [ a , b ], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f ( x 1 ) = m , f ( x 2 ) = M , причем
m £ f ( x ) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f ( x ) = sinx ).
|
|
|
Дата добавления: 2019-02-12; просмотров: 138; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!