Производная функции, ее геометрический и механический смыслы.

Производная функции, ее геометрический и физический смысл.

Определение. Производной функции f ( x ) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

F ( x )

f ( x ₀ + D x ) P

D f

f ( x ₀ ) M

A b D x

x ₀ x ₀ + D x x

Пусть f ( x ) определена на некотором промежутке (a, b ). Тогда тангенс угла наклона секущей МР к графику функции.

где a - угол наклона касательной к графику функции f ( x ) в точке ( x ₀ , f ( x ₀ )).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

Уравнение нормали к кривой: .

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f ( t ), где t - время, а f ( t )- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

Односторонние производные. Производная сложной и обратной функции.

Односторонние производные функции в точке.

Определение. Правой (левой) производной функции f ( x ) в точке х = х₀ называется правое (левое) значение предела отношения при условии, что это отношение существует.

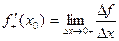
Если функция f ( x ) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во-первых функция может иметь разрыв в точке х₀, а во-вторых, даже если функция непрерывна в точке х₀, она может быть в ней не дифференцируема.

Например: f ( x ) = ï x ï - имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема. (Необходимое условие существования производной) Если функция f ( x ) имеет производную в точке х₀, то она непрерывна в этой точке.

Понятно, что это условие не является достаточным.

Производная сложной функции.

Теорема. Пусть y = f ( u ); u = g ( x ), причем область значений функции u входит в область определения функции f .

Тогда

Доказательство.

( с учетом того, что если D x ® 0, то D u ® 0, т.к. u = g ( x ) – непрерывная функция)

Тогда

Теорема доказана.

Производная обратных функций.

Пусть требуется найти производную функции у = f ( x ) при условии, что обратная ей функция x = g ( y ) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g ( y ) по х:

т.к. g ¢ ( y ) ¹ 0

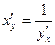
Т.е. производная обратной функции обратна по величине производной данной функции.

Пример. Найти формулу для производной функции arctg .

Функция arctg является функцией, обратной функции tg , т.е. ее производная может быть найдена следующим образом:

Известно, что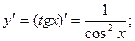

По приведенной выше формуле получаем:

Т.к. то можно записать окончательную формулу для производной арктангенса:

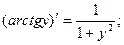
Дата добавления: 2019-02-12; просмотров: 189; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 16 17 18 19 202122 23 24 25 Следующая ⇒

Мы поможем в написании ваших работ!