Предел функции в бесконечности. Геометрическая иллюстрация.
Определение. Число А называется пределом функции f ( x ) при х ® ¥ , если для любого числа e >0 существует такое число М>0, что для всех х, ï х ï > M выполняется неравенство
При этом предполагается, что функция f ( x ) определена в окрестности бесконечности.
Записывают: 
Графически можно представить:
 |
Y y
A A
0 0
X x
y y
 |
A A
0 0
X x
Аналогично можно определить пределы 
для любого х> M и
для любого х< M .
Бесконечно малые функции и их свойства. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими функциями.
Бесконечно малые функции.
Определение. Функция f ( x ) называется бесконечно малой при х ® а, где а может быть числом или одной из величин ¥ , + ¥ или - ¥ , если 
.
|
|
|
Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.
Теорема. Для того, чтобы функция f ( x ) при х ® а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f ( x ) = A + a ( x ),
где a (х) – бесконечно малая при х ® а ( a (х) ® 0 при х ® а).
Свойства бесконечно малых функций:
1) Сумма фиксированного числа бесконечно малых функций при х ® а тоже бесконечно малая функция при х ® а.
2) Произведение фиксированного числа бесконечно малых функций при х ® а тоже бесконечно малая функция при х ® а.
3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х ® а.
Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.
Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.
Доказательство теоремы 2. Представим f ( x ) = A + a ( x ), g ( x ) = B + b ( x ), где
|
|
|
, тогда
f(x) ± g(x) = (A + B) + a (x) + b (x)
A + B = const , a (х) + b (х) – бесконечно малая, значит
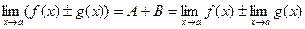
Бесконечно большие функции и их связь с
Бесконечно малыми.
Определение. Предел функции f ( x ) при х ® а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D >0, что неравенство
ï f ( x ) ï > M
Выполняется при всех х, удовлетворяющих условию
0 < ï x - a ï < D
Записывается 
.
Собственно, если в приведенном выше определении заменить условие ï f ( x ) ï > M на f ( x )> M , то получим:
а если заменить на f ( x )< M , то:
Графически приведенные выше случаи можно проиллюстрировать следующим образом:
 |
A x a x a x
Определение. Функция называется бесконечно большой при х ® а, где а – чосли или одна из величин ¥ , + ¥ или - ¥ , если 
, где А – число или одна из величин ¥ , + ¥ или - ¥ .
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f ( x ) ® 0 при х ® а (если х ® ¥ ) и не обращается в ноль, то
30. Основные теоремы о пределах.
|
|
|
Теорема 1. 
, где С = const .
Следующие теоремы справедливы при предположении, что функции f ( x ) и g ( x ) имеют конечные пределы при х ® а.
Теорема 2. 
Дата добавления: 2019-02-12; просмотров: 357; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!