Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [ a , b ], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f ( x ) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f ( x )- непрерывная на отрезке [ a , b ] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f ( x ) = 0.
Т . е . если sign(f(a)) ¹ sign(f(b)), то $ х 0 : f(x0) = 0.
Определение. Функция f ( x ) называется равномерно непрерывной на отрезке [ a , b ], если для любого e >0 существует D >0 такое, что для любых точек х1 Î [ a , b ] и x 2 Î [ a , b ] таких, что
ï х2 – х1 ï < D
верно неравенство ï f ( x 2 ) – f ( x 1 ) ï < e
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D , не зависящее от х, а при “обычной” непрерывности D зависит от e и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример. 
Функция 
непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D >0 такое, что существуют значения х1 и х2 такие, что ï f ( x 1 ) – f ( x 2 ) ï > e , e - любое число при условии, что х1 и х2 близки к нулю.
|
|
|
Свойство 7: Если функция f ( x ) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g ( y ) тоже однозначна, монотонна и непрерывна.
III . Дифференциальное исчисление функции одной переменной.
Задачи, приводящие к определению производной.
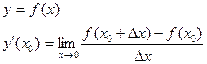
Производной в точке 
называется предел отношения приращения функции к приращению аргумента, когда это приращение аргумента стремиться к 0.
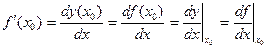
При каждом конкретном числовом значении 
производная представляет собой определенное число.
Возникает некоторая функциональная зависимость, поэтому производная является функцией аргумента 
.
Если производная в точке равна 
, то говорят, что производная в точке бесконечна или конечной производной в точке не существует.
Если в определении производной потребовать дополнительно чтобы 
, то придем к понятию левосторонней производной.
Если в определении потребовать, чтобы 
, то – правосторонняя производная.
Левосторонняя и правосторонняя производные называются односторонними производными.
Операцию нахождения производной называют дифференцированием.
|
|
|
Из свойств пределов следует, что если в точке существует производная от функции 
, то она равна односторонним производным в этой точке.
Пример. Найти производную от 
Дата добавления: 2019-02-12; просмотров: 219; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!