Основные правила дифференцирования.
Основные правила дифференцирования.
Обозначим f ( x ) = u , g ( x ) = v - функции, дифференцируемые в точке х.
1) ( u ± v ) ¢ = u ¢ ± v ¢
А) 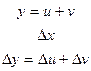
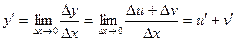
Б) 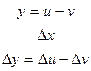
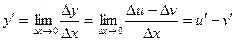
2) ( u × v ) ¢ = u × v ¢ + u ¢ × v
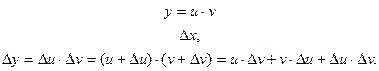
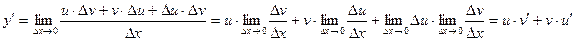
3) 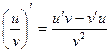 , если v ¹ 0
, если v ¹ 0
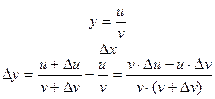
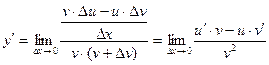
4) 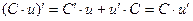
Эти правила могут быть легко доказаны на основе теорем о пределах.
Основные формулы дифференцирования.
Производные основных элементарных функций.
1)С ¢ = 0; 9) 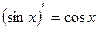
2)( xm ) ¢ = mxm -1 ; 10) 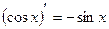
3) 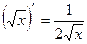 11)
11) 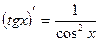
4) 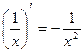 12)
12) 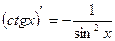
5) 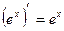 13)
13) 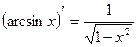
6) 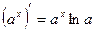 14)
14) 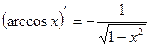
7) 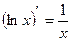 15)
15) 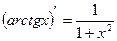
8) 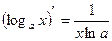 16)
16) 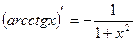
Дифференциал функции и его геометрический смысл.
Дифференциал функции.
Пусть функция y = f ( x ) имеет производную в точке х:
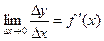
Тогда можно записать: 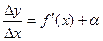 , где a ® 0, при D х ® 0.
, где a ® 0, при D х ® 0.
Следовательно: 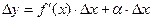 .
.
Величина a D x - бесконечно малая более высокого порядка, чем f ¢ ( x ) D x , т.е. f ¢ ( x ) D x - главная часть приращения D у.
Определение. Дифференциалом функции f ( x ) в точке х называется главня линейная часть приращения функции. (или произведение производной этой функции на приращение независимой переменной).
Обозначается dy или df ( x ).
Из определения следует, что dy = f ¢ ( x ) D x или
dy = f ¢ ( x ) dx .
Можно также записать: 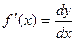
|
|
|
Геометрический смысл дифференциала.
 y
y
F ( x )
K
Dy
M D y
L
A
x x + D x x
Из треугольника D MKL : KL = dy = tg a × D x = y ¢ × D x
Таким образом, дифференциал функции f ( x ) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала и инвариантность его формулы. Применение дифференциала к приближенным вычислениям.
Свойства дифференциала.
Если u = f ( x ) и v = g ( x )- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v) ¢ dx = u ¢ dx ± v ¢ dx = du ± dv
2) d(uv) = (uv) ¢ dx = (u ¢ v + v ¢ u)dx = vdu + udv
3) d(Cu) = Cdu
4) 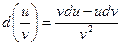
Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f ( x ), x = g ( t ), т.е. у - сложная функция.
Тогда dy = f ¢ ( x ) g ¢ ( t ) dt = f ¢ ( x ) dx .
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
|
|
|
Однако, если х - независимая переменная, то
dx = D x , но
если х зависит от t , то D х ¹ dx .
Таким образом, форма записи dy = f ¢ ( x ) D x не является инвариантной.
Пример. Найти производную функции 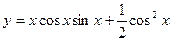 .
.
Сначала преобразуем данную функцию: 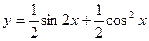
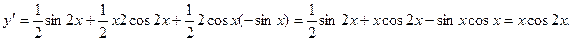
Применение дифференциала к приближенным вычислениям.
Дифференциал функции y = f ( x ) зависит от D х и является главной частью приращения D х.
Также можно воспользоваться формулой
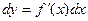
Предел 2х бесконечно малых функций равен 1, значит 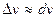 - приращение функции эквивалентно дифференциалу. Это равенство и есть основа для приближенных вычислений.
- приращение функции эквивалентно дифференциалу. Это равенство и есть основа для приближенных вычислений.
Тогда абсолютная погрешность
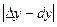
Относительная погрешность
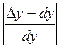
Формально дифференциал от производной отличается только сомножителем 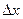 . Поэтому при практическом вычислении дифференциалов пользуются таблицами и правилами производных и формально приписывают сомножитель
. Поэтому при практическом вычислении дифференциалов пользуются таблицами и правилами производных и формально приписывают сомножитель 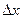 .
.
Дата добавления: 2019-02-12; просмотров: 203; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
