Доказательство этой теоремы будет приведено ниже.
Теорема 3. 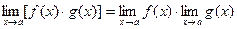
Следствие. 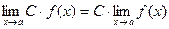
Теорема 4. 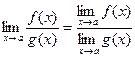 при
при 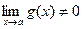
Теорема 5. Если f ( x )>0 вблизи точки х = а и 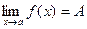 , то А>0.
, то А>0.
Аналогично определяется знак предела при f ( x ) < 0, f( x ) ³ 0, f( x ) £ 0.
Теорема 6. Если g ( x ) £ f ( x ) £ u ( x ) вблизи точки х = а и 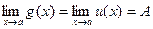 , то и
, то и 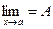 .
.
Определение. Функция f ( x ) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ï f ( x ) ï < M вблизи точки х = а.
Теорема 7. Если функция f ( x ) имеет конечный предел при х ® а, то она ограничена вблизи точки х = а.
Доказательство. Пусть 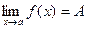 , т.е.
, т.е. 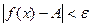 , тогда
, тогда
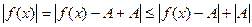 или
или
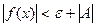 , т.е.
, т.е.
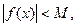 где М = e + ï А ï
где М = e + ï А ï
Теорема доказана.
Свойства эквивалентных бесконечно малых.
1) a ~ a , 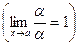
2) Если a ~ b и b ~ g , то a ~ g , 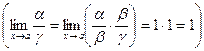
3) Если a ~ b , то b ~ a , 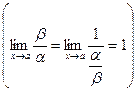
4) Если a ~ a 1 и b ~ b 1 и 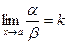 , то и
, то и 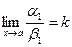 или
или 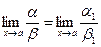 .
.
Следствие: а) если a ~ a 1 и 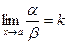 , то и
, то и 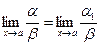
б) если b ~ b 1 и 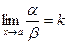 , то
, то 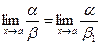
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.
Первый и второй замечательные пределы.
Некоторые замечательные пределы.
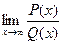 , где P(x) = a0xn + a1xn-1 +…+an,
, где P(x) = a0xn + a1xn-1 +…+an,
Q ( x ) = b 0 xm + b 1 xm -1 +…+ bm - многочлены.
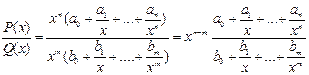
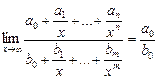
Итого: 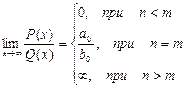
Первый замечательный предел. 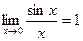
|
|
|
Второй замечательный предел. 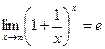
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
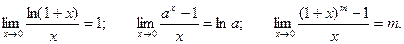
Пример. Найти предел.
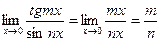
Пример. Найти предел.
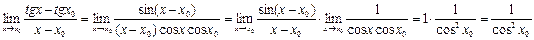
Сравнение бесконечно малых функций.
Пусть a (х), b (х) и g (х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a , b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f ( x ) = x 10 стремится к нулю быстрее, чем функция f ( x ) = x .
Определение. Если 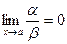 , то функция a называется бесконечно малой более высокого порядка, чем функция b .
, то функция a называется бесконечно малой более высокого порядка, чем функция b .
Определение. Если 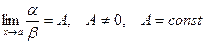 , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если 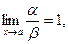 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b .
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b .
Пример. Сравним бесконечно малые при х ® 0 функции f ( x ) = x 10 и f ( x ) = x .
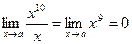
т.е. функция f ( x ) = x 10 – бесконечно малая более высокого порядка, чем f ( x ) = x .
|
|
|
Определение. Бесконечно малая функция a называется бесконечно малой порядка k относительно бесконечно малой функции b , если предел 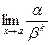 конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 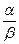 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если 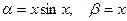 , то при х ® 0
, то при х ® 0 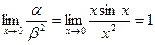 , т.е. функция a - бесконечно малая порядка 2 относительно функции b .
, т.е. функция a - бесконечно малая порядка 2 относительно функции b .
Пример. Если 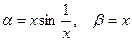 , то при х ® 0
, то при х ® 0 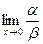 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
33. Непрерывность функций в точке и на отрезке. Точки разрыва функции и их классификация.
Дата добавления: 2019-02-12; просмотров: 162; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
