Функции только убывающие или только возрастающие называются монотонными.
4. Функцию 
, определенную на множестве 
, называют ограниченной на этом множестве, если существует такое число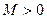 
, что для всех 
выполняется неравенство 
(короткая запись: 
, 
, называется ограниченной на , если 
). Отсюда следует, что график ограниченной функции лежит между прямыми 
и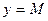 
.
24. Гиперболические функции, их свойства и графики.
К ним относятся:
- гиперболический косинус и
- гиперболический синус.
С помощью этих функций можно определить еще 2 функции:
- гиперболический тангенс и
- гиперболический котангенс.
Функции 
определены, очевидно, для всех значений 
. Функция же 
определена всюду, за исключением точки 
.
Из определения функци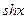й 
и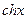 
следуют соотношения, аналогичные соотношениям между соответствующими тригонометрическими функциями:
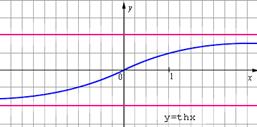
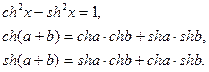
Название "гиперболические функции" объясняется тем, что функции 
и 
играют ту же роль для параметрического представления гиперболы
какую тригонометрические функции 
и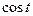 
- для параметрического представления окружности 
Производные гиперболических функций определяются формулами:
Числовые последовательности. Предел числовой последовательности.
Определение. Если каждому натуральному числу n поставлено в соответствие число х n , то говорят, что задана последовательность
x1, х2, …, х n = { xn }
Общий элемент последовательности является функцией от n .
|
|
|
xn = f ( n )
Таким образом, последовательность может рассматриваться как функция порядкового номера элемента.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Пример. { xn } = {(-1) n } или { xn } = -1; 1; -1; 1; …
{ xn } = { sin p n /2} или { xn } = 1; 0; 1; 0; …
Для последовательностей можно определить следующие операции :
1) Умножение последовательности на число m : m { xn } = { mxn }, т.е. mx 1 , mx 2 , …
2) Сложение (вычитание) последовательностей: { xn } ± { yn } = { xn ± yn }.
3) Произведение последовательностей: { xn } × { yn } = { xn × yn }.
4) Частное последовательностей : 
при {yn} ¹ 0.
Ограниченные и неограниченные последовательности.
Определение. Последовательность { xn } называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:
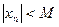
Т.е. все члены последовательности принадлежат промежутку (-М; M ).
Определение. Последовательность { xn }называется ограниченной сверху, если для любого n существует такое число М, что
xn £ M .
Определение. Последовательность { xn }называется ограниченной снизу, если для любого n существует такое число М, что
|
|
|
xn ³ M
Пример. { xn } = n – ограничена снизу {1, 2, 3, … }.
Определение. Число а называется пределом последовательности { xn }, если для любого положительного e >0 существует такой номер N , что для всех n > N выполняется условие:
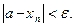
Это записывается: lim xn = a .
В этом случае говорят, что последовательность { xn }сходится к а при n ® ¥ .
Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.
Пример. Доказать, что предел последовательности lim 
.
Пусть при n > N верно 
, т.е.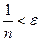 
. Это верно при 
, таким образом, если за N взять целую часть от 
, то утверждение, приведенное выше, выполняется.
Теорема. Последовательность не может иметь более одного предела.
Теорема. Если xn ® a , то 
.
Теорема. Если xn ® a , то последовательность { xn } ограничена.
Дата добавления: 2019-02-12; просмотров: 183; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!