Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например, последовательность 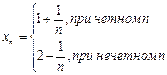 не имеет предела, хотя
не имеет предела, хотя 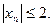
Число е. натуральные логарифмы.
Рассмотрим последовательность { xn } = 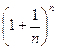 .
.
Если последовательность { xn } монотонная и ограниченная, то она имеет конечный предел.
По формуле бинома Ньютона:
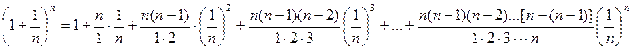 или, что то же самое
или, что то же самое
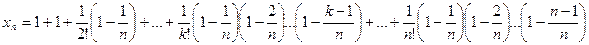
Покажем, что последовательность { xn } – возрастающая. Действительно, запишем выражение xn +1 и сравним его с выражением xn :
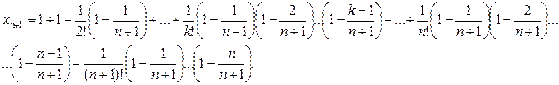 Каждое слагаемое в выражении xn +1 больше соответствующего значения xn , и, кроме того, у xn +1 добавляется еще одно положительное слагаемое. Таким образом, последовательность { xn } возрастающая.
Каждое слагаемое в выражении xn +1 больше соответствующего значения xn , и, кроме того, у xn +1 добавляется еще одно положительное слагаемое. Таким образом, последовательность { xn } возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.
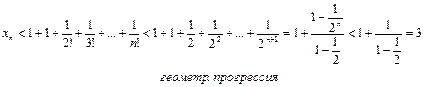
Итак, последовательность 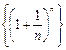 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
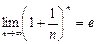
Из неравенства 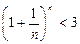 следует, что е £ 3. Отбрасывая в равенстве для { xn } все члены, начиная с четвертого, имеем:
следует, что е £ 3. Отбрасывая в равенстве для { xn } все члены, начиная с четвертого, имеем:
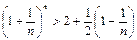
Переходя к пределу, получаем
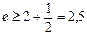
Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.
Можно показать, что число е иррациональное и его значение равно 2,71828…
Аналогично можно показать, что 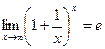 , расширив требования к х до любого действительного числа:
, расширив требования к х до любого действительного числа:
Предположим: 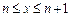
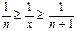

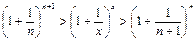
Найдем 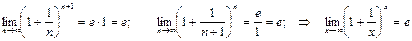
Число е является основанием натурального логарифма.
|
|
|
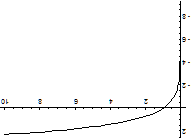

Выше представлен график функции y = lnx .
Связь натурального и десятичного логарифмов.
Пусть х = 10у, тогда lnx = ln 10 y , следовательно lnx = yln 10
у = 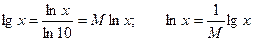 , где М = 1/ ln 10 » 0,43429…- модуль перехода.
, где М = 1/ ln 10 » 0,43429…- модуль перехода.
 27. Предел функции в точке, односторонние пределы. Геометрическая иллюстрация определений.
27. Предел функции в точке, односторонние пределы. Геометрическая иллюстрация определений.
Y f ( x )
A + e
A
A - e
0 a - D a a + D x
Пусть функция f ( x ) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
Определение. Число А называется пределом функции f ( x ) при х ® а, если для любого e >0 существует такое число D >0, что для всех х таких, что
0 < ï x - a ï < D
верно неравенство ï f ( x ) - A ï < e .
То же определение может быть записано в другом виде:
Если а - D < x < a + D , x ¹ a , то верно неравенство А - e < f ( x ) < A + e .
Запись предела функции в точке: 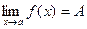
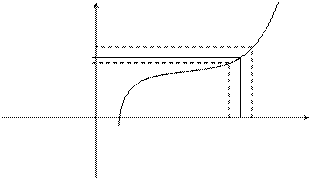
Определение. Если f ( x ) ® A 1 при х ® а только при x < a , то 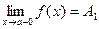 - называется пределом функции f ( x ) в точке х = а слева, а если f ( x ) ® A 2 при х ® а только при x > a , то
- называется пределом функции f ( x ) в точке х = а слева, а если f ( x ) ® A 2 при х ® а только при x > a , то 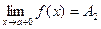 называется пределом функции f ( x ) в точке х = а справа.
называется пределом функции f ( x ) в точке х = а справа.
|
|
|
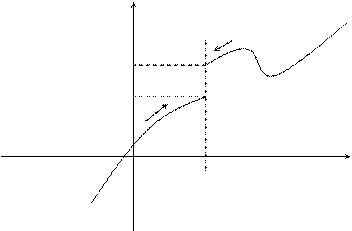 у
у
F ( x )
А2
А1
A x
Приведенное выше определение относится к случаю, когда функция f ( x ) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А1 и А2 называются также односторонними пределами функции f ( x ) в точке х = а. Также говорят, что А – конечный предел функции f ( x ).
Дата добавления: 2019-02-12; просмотров: 210; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
