ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Функция называется периодической, если существует такое число λ ≠0, что при любом α из области определения функции числа α - λ и α + λ. также принадлежат этой области и выполняется равенство
f (α - λ )= f (α)= f (α + λ ).
В этом случае число λ называется периодом функции f; ее периодами являются также числа вида п λ, nЄ Z, п≠О. Наименьший положительный период для синуса и косинуса равен 2π, а для тангенса и котангенса он равен π.
Свойство периодичности тригонометрических функций можно выразить тождествами:
sin α =sin(α - 2πk), k Є Z ; (16)
сos α=cos(α +2 πk), kЄ Z; (17)
tg α =tg(α + πk), kЄ Z; (18)
ctg α =ctg(α + πk), kЄ Z. (19)
1. Вычислить:
l) cos 3660°; 2) 2cos4,5π+sin(19π/3); 3) sin(-300°)-tg(-150°).
На основании свойства периодичности косинуса и синуса получим:
1) cos 3660°=cos (360° • 10+60°)=cos 60° = 1/2;
2) 2 cos 4,5π+sin (19π/3) = 2 cos (2π • 2+0,5π)+sin (2π • 3+π/3) = 2 cos 0,5π +
+sin (π/3) =0+ 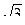 /2 =
/2 = 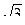 /2
/2
3) Прибавив по одному периоду к каждому из аргументов, получим
|
|
|
sin (- 300°) - tg (-150°)=sin ( - 300° + 360°) - tg ( -150° +180°) = sin60е-tg30°=
= 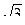 /2 -
/2 - 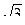 /3 =
/3 = 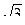 /6.
/6.
1. Найти периоды функций: 1) y=sin3x; 2) y=cos(x/2).
1) Обозначив искомый период через λ, получим
sin 3 (х+ λ) = sin Зх, или sin(3x+3 λ) = sin3x.
Отсюда заключаем, что З λ =2 π, т. е. λ =2 π /3.
2) Аналогично имеем
cos= (  )=cos
)=cos  , или cos(
, или cos(  +
+ 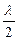 ) = cos
) = cos  ,
,
откуда λ /2=2 π, т. е. λ =4 π.
2. Найти периоды функций:
1) y=sin2x+cos3x; 2) y=sin(3x/2)+sin(2x/3).
1) Найдем период каждого из слагаемых:
sin 2 (х+ λ1)=sin 2х, sm(2x+2 λ1) = sin2x, 2 λ1=2 π, λ1 = π ;
cos3(x+ λ 2)=cos3x, cos(3x+3 λ 2) = cos3x, З λ 2 = 2 π, λ 2 = 2 π /3.
Каждое число, кратное периоду, само является периодом, поэтому общее кратное чисел λ1 и λ 2является периодом функции у. Наименьшее общее кратное чисел π и
2π/3, равное наименьшему общему кратному числителей периодов λ1 и λ 2, есть 2π.
2) Имеем
sin 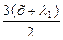 = sin
= sin 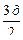 , sin(
, sin( 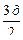 +
+ 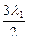 )=sin
)=sin  , 3 λ 1 /2, λ 1 =4π/3
, 3 λ 1 /2, λ 1 =4π/3
sin 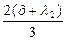 = sin
= sin 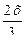 , sin(
, sin(  +
+  )=sin
)=sin  , 2 λ 2 /3, λ 2 =3π.
, 2 λ 2 /3, λ 2 =3π.
Наименьшее общее кратное числителей периодов λ1, и λ2 равно 12 π;
следовательно, период функции равен 12 π.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Функция y=sin x на отрезке - π /2≤х≤ π /2 имеет обратную функцию, которая называется арксинусом и обозначается y = arcsin х:
|
|
|
-1 ≤ D (arcsin х) ≤1, - π /2 ≤ E (arcsin х) ≤ π /2;
sin (arcsin х) = х, где -1 ≤ х ≤ 1: arcsin( - х) = - arcsin х.
Функция y=cos x на отрезке 0≤x≤ π имеет обратную функцию, которая называется арккосинусом и обозначается у = arccos х:
- 1 ≤ D (arccos x) ≤ 1, 0 ≤ E(arccos x) ≤ π;
cos (arccos x) = x, где - 1 ≤ x ≤1 arccos (-x) = π - arccos x.
Функция y=tgx на промежутке - π /2<х< π /2 имеет обратную функцию, которая называется арктангенсом и обозначается у= arctg х:
D (arctg x) = R, - π /2 < E(arctg х) < π /2;
tg(arctg x) = x, где x Є R; arctg(-х)= - arctg х.
Функция y=ctg x на промежутке 0<х< π имеет обратную функцию которая называется арккотангенсом и обозначается y = arcctgx:
D (arcctg x) = R, 0<E(arcctg x)< π;
ctg(arcctg x) = x, где x Є R; arcctg( -х)= π - arcctgx.
1. Проверить, справедливы ли равенства: 1) arcsin(1/2)= π /6;
2) arccos (- 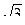 /2) = 5 π /6; 3) arctg
/2) = 5 π /6; 3) arctg 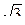 = - π /3.
= - π /3.
1) arcsin (1/2) = π /6, так как sin (π /6) =1/2 и - π /2 < π /6- π/2,
2) arccos (- 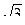 /2) = 5 π /6, так как соs(5 π /6)= -
/2) = 5 π /6, так как соs(5 π /6)= - 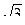 /2 и 0<5π/6< π;
/2 и 0<5π/6< π;
3) arctg 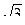 = - π /3, так как tg (-π /3) = -
= - π /3, так как tg (-π /3) = - 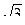 и - π /2 < - π /3 < π /2.
и - π /2 < - π /3 < π /2.
|
|
|
Формулы приведения
Правило:
Для углов (  ±α) или (
±α) или (  ±α) в формулах приведения тригонометрическая функция меняется на ко – функцию, а знак зависит от того какой знак имела первоначальная функция в данной четверти.
±α) в формулах приведения тригонометрическая функция меняется на ко – функцию, а знак зависит от того какой знак имела первоначальная функция в данной четверти.
Для углов (  ±α) или (2
±α) или (2  ±α) в формулах приведения тригонометрическая функция не меняется, а знак зависит от того какой знак имела эта функция в данной четверти.
±α) в формулах приведения тригонометрическая функция не меняется, а знак зависит от того какой знак имела эта функция в данной четверти.
1. 1) sin225°; 2)'cos 150°; 3) tg210°; 4) sin330°; 5)tg315°; 6) cos 240°; 7) sin 200°;
8) ctg 140°.
1) sin225o = sin(180°+45o)=-sin45°=- 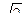 /2;
/2;
2) cosl50o=cos(180o-30°)=-cos30°= - 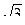 /2;
/2;
3) tg 210° = tg (180° + 30°) = tg 30° = 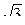 /3;
/3;
4) sin 330° = sin (360° - 30°) = - sin 30° = -1 /2;
5) tg315o=tg(360o-45°)=-tg45°= - l;
6) ros240o=cos(180° + 60o)=-cos60°= - l/2;
7) sin 200° = sin (180° + 20°) = - sin 20° = - 0,3420;
8) ctg 140°=ctg(180°-40°)=-ctg40° = -1,1918. •
2. 1) sin 2,15; 2) tg4,85.
1) sin2,15=sin(3,14-0,99) = sin0,99 = sin57°=0,84;
2) tg4,85 = tg(4,85 - 3,14) = tg l,71=tg(l,57+0,14)=-ctg0,14 =-ctg8°=-7,l.
Дата добавления: 2019-01-14; просмотров: 359; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
