ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА
Формулы для тригонометрических функций половинного аргумента позволяют выразить функции аргумента  /2 через функции аргумента
/2 через функции аргумента  :
:
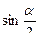 =
=  ; (32)
; (32)
 =
=  ; (33)
; (33)
 =
= 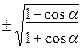 ;
; 
 ; (34)
; (34)
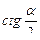 =
=  ,
,  ; (35)
; (35)
 =
=  ,
, 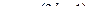 (36)
(36)
 =
=  , в левой части
, в левой части 
 , (37)
, (37)
в правой части 
 ;
;
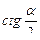 =
=  , , в левой части
, , в левой части 
 , (38)
, (38)
в правой части 
 ;
;
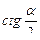 =
=  ,
, 
 . (39)
. (39)
В формулах знак перед корнем определяется по знаку четверти, которой принадлежит дуга  /2, или чтобы он совпадал со знаком tg(
/2, или чтобы он совпадал со знаком tg(  /2), т. е. ставится плюс, если
/2), т. е. ставится плюс, если  /2—дуга I или III четверти, и минус, если
/2—дуга I или III четверти, и минус, если  /2—дуга II или IV четверти.
/2—дуга II или IV четверти.
Все тригонометрические функции любого аргумента можно выразить через тангенс половины этого аргумента по формулам

 ,
, 
 ; (40)
; (40)
cos  =
=  ;
; 
 ; (41)
; (41)
tg  =
= 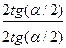 ,
, 
 ,
, 
 (42)
(42)
ctg  =
=  ;
; 
 . (43)
. (43)
1. Дано: cos  =1/2 и
=1/2 и  /2<
/2<  <
<  . Вычислить sin (
. Вычислить sin (  /2), cos (
/2), cos (  /2) и tg(
/2) и tg(  /2).
/2).
1) По формулам находим
sin  =
= 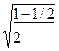 =
= 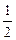 ; cos
; cos  =
= 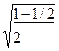 =
= 
(перед корнем в обоих случаях ставим плюс, так как из условия следует, что  /4<
/4<  /2<
/2<  /2). Далее, имеем tg(
/2). Далее, имеем tg(  /2)=(l/2);(
/2)=(l/2);( 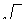 3/2)= 1/
3/2)= 1/  3=
3=  3/3. •
3/3. •
2. Вычислить tg(  /2), если: 1) sin
/2), если: 1) sin  =4/5 и
=4/5 и  /2<
/2<  <
<  ; 2) cos
; 2) cos  = -4/5 и
= -4/5 и  <
<  <3
<3  /2;
/2;
3) tg  =2
=2  2 и
2 и  <
<  <3
<3  /2.
/2.
1) Находим cos  = -
= -  = -3/5. По формуле получим
= -3/5. По формуле получим
tg  =
=  :(1-
:(1-  ) = 2.
) = 2.
2). Находим sin  = -
= - 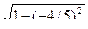 = -3/5 По формуле получим
= -3/5 По формуле получим
tg  =
=  :(1-
:(1-  ) = -3
) = -3
3) Вычисляем sin  и cos
и cos  :
:
sin  = -
= -  = -
= - 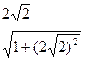 = -
= -  .
.
cos  =-
=-  = -
= - 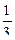 .
.
По формуле получим 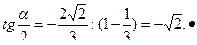
3. Вычислить: 1) sin  , если tg(
, если tg(  /2) = 2; 2) cos
/2) = 2; 2) cos  , если tg(
, если tg(  /2)=3; 3) tg
/2)=3; 3) tg  , если tg(
, если tg(  /2)=
/2)= 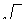 3; 4) ctg
3; 4) ctg  , если tg(
, если tg(  /2)= -
/2)= - 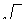 2; 5)
2; 5) 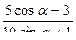 ,
,
Используя формулы, получим:
1). sin  =
=  ;
;
2).cos  =
=  ;
;
3). tg  =
=  ;
;
4). ctg  =
=  ;
;
5). сos  =
= 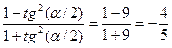 ; sin
; sin  =
=  ;
;
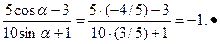
4 Решить уравнения: 1) sin( 
2). sinx+cosx=1; 3).3sinx+4cosx=4
1) 

 Ответ:
Ответ:  ;
; 

2). 
ó 
 Ответ:
Ответ: 
3).Выразим sinx и cosx через z=tg(x/2); имеем 

 тогда
тогда

Данное уравнение равносильно совокупности уравнений tg(x/2)=0 и tg(x/2)=3/4, откуда х/2 =  k и х/2 = arctg (3/4)+
k и х/2 = arctg (3/4)+  k. Ответ: 2
k. Ответ: 2  k; 2 arctg (3/4) + 2
k; 2 arctg (3/4) + 2  k.
k.
Преобразование произведения тригонометрических функций в сумму
Для преобразования произведения тригонометрических функций в сумму применяются формулы
sin  cos
cos  =
=  [sin (
[sin (  +
+  ) + sin (
) + sin (  -
-  )]; (44)
)]; (44)
cos  cos
cos  =
=  [cos (
[cos (  +
+  )+ cos (
)+ cos (  -
-  )]; (45)
)]; (45)
sin  sin
sin  =
=  [cos (
[cos (  -
-  ) - cos (
) - cos (  +
+  )]. (46)
)]. (46)
1. Преобразовать в алгебраическую сумму:
1) sin5x sin3x; 2) cos 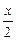 cos
cos  cos
cos 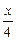 .
.
1) По формуле (9.60) получим
sin 5х sin Зх =  (cos (5х - Зх) - cos (5х+Зх)) =
(cos (5х - Зх) - cos (5х+Зх)) =  cos 2х -
cos 2х -  cos 8х.
cos 8х.
2) Используя дважды формулу (9.59), получим
cos 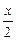 cos
cos  cos
cos 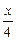 =(cos
=(cos 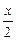 cos
cos 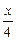 )cos
)cos  =
=  (cos
(cos  +cos
+cos 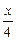 )cos
)cos  =
=  (cos
(cos  cos
cos  + cos
+ cos 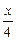 cos
cos  )=
)=  (
(  (cos
(cos  +cos
+cos  )+
)+  (cos
(cos  +cos
+cos  ))=
))= 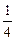 cos
cos  +
+ 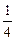 cos
cos  +
+ 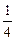 cos
cos  +
+ 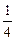 cos
cos 

2. Представить в виде сумм первых степеней следующие тригонометрические функции: 1) sin2x; 2) cos2x; 3) sin3x.
1) sin2x=sinx sinx=  (cos 0—cos2x)=
(cos 0—cos2x)=  -
-  cos2x;
cos2x;
2) cos2x = cosx cosx=  (cos0+cos2x) =
(cos0+cos2x) =  +
+  cos2x;
cos2x;
3) sin3x = sin2x sinx=(  -
-  cos2x) sinx =
cos2x) sinx =  sinx -
sinx -  sinxcos2x=
sinxcos2x=  sinx-
sinx- 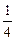 (sin3x-sinx)=
(sin3x-sinx)=  sinx-
sinx- 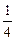 sin3x+
sin3x+ 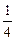 sinx =
sinx =  sinx -
sinx - 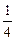 sin3x.
sin3x.
Отсюда получаем формулу для синуса утроенного аргумента: sin3x = = 3sinx—4sin3x. •
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКОЙ СУММЫ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В ПРОИЗВЕДЕНИЕ
1. Основные формулы. Для преобразования алгебраических сумм тригонометрических функций в произведение (приведения к виду, удобному для логарифмирования) используются формулы
 (47)
(47)
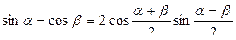 (48)
(48)
 (49)
(49)
 (50)
(50)


 (51)
(51)
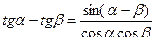

 (52)
(52)
Часто используются также следующие формулы:
 (53)
(53)
 (54)
(54)
 (55)
(55)
 (56)
(56)
2. Условия равенства одноименных тригонометрических функций. Для
того чтобы синусы двух аргументов были равны, необходимо и достаточно выполнение следующих условий:
(sin x = sin у) 
Для того чтобы косинусы двух аргументов были равны, необходимо и достаточно выполнение следующих условий:
(cos x =cos y) 
Для того чтобы тангенсы двух аргументов были равны, необходимо и достаточно выполнение следующих условий:
(tg x= tg y) 
Преобразовать в произведение:
1. 1) sin 40° + sin 20'; 2) cos (π/5)-cos (7 π /10); 3) ctg(2 π /7)-ctg(π /7);
4) cos2 α-sin2 β; 5) sin 2 α cos 3 α -2 sin2 α sin 3 α.
1) По формуле (9.61) получим
sin 40° + sin 20° = 2 sin  cos
cos  =
=
= 2 sin 30° cos 10° =  cos 10° = cos 10°.
cos 10° = cos 10°.
2) По формуле (9.64) получим
cos (π /5) - cos (7 π /10) = 2 sin (9 π /20) sin (π /4)=  sin (9 π /20).
sin (9 π /20).
3) Выразив котангенсы через тангенсы, используем формулу (9.66):
ctg (2 π /7) - ctg (π /7) = tg (π /2 - 2 π /7) - tg (π /2 - π /7) =
=tg (3 π/14)-tg(5 π/14)= - 
4) Используя формулы (9.67), (9.68) и (9.63), получим
cos2 α-sin2 β =(  )-(
)-(  )=
)=  (cos2 α-cos 2β)=
(cos2 α-cos 2β)=
=  2cos
2cos 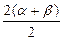 cos
cos  =cos (α+β)cos (α-β)
=cos (α+β)cos (α-β)
5) sin 2 α cos 3 α - 2 sin2 α sin 3 α = 2 sin α cos α cos 3 α - 2 sin2 α sin 3 α =
= 2 sin α (cos α cos 3 α —sin α sin 3α) = 2 sin α cos 4 α.
2. 1) 1+sin α +cos α; 2) sinx+sin2x + sin3x,
3) sin 20° +sin 34° +sin 24° +sin 30°.
1) Преобразуя выражение 1+cos α в произведение по формуле и используя формулу удвоенного аргумента для sin α, получим
l+cosα+sinα=2cos2  +2sin
+2sin  cos
cos  =2cos
=2cos  ( cos
( cos  + sin
+ sin  )= 2cos
)= 2cos  ( cos
( cos  +cos(
+cos(  -
-  )) = =4cos
)) = =4cos  cos
cos  cos(
cos(  -
-  ) =2
) =2  cos
cos  cos(
cos(  -
-  ).
).
2) Преобразуем в произведение сумму двух первых слагаемых (можно любых двух слагаемых), а третье слагаемое преобразуем по формуле удвоенного аргумента:
sin х + sin 2х + sin Зх=2 sin  cos
cos  + 2sin
+ 2sin  cos
cos  = 2 sin
= 2 sin  ( cos
( cos  +cos
+cos  ) =
) =
=2 sin  2 cos x cos
2 cos x cos  = 4 sin
= 4 sin  cos x cos
cos x cos  .
.
3) Заметив, что 20° + 34° = 24° + 30o, выполним последовательно преобразования по формулам (9.61) и (9.63):
sin 20° + sin 34°+sin 24° + sin 30° = 2 sin 27° cos 7° +
+ 2 sin 27° cos 3° = 2 sin 27° (cos 7°+cos 3°) = 4 sin 27° cos 5° cos 2°.
3. Решить уравнения: 1) sin4x = sin3x; 2) cos5x=cos(x-  );
);
3) cosx = sin3x; 4) tg5x = tgx.
Воспользуемся условиями равенства одноименных тригонометрических функций:
1) (sin4x=sin3x) 


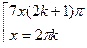 Ответ :(2k+1)
Ответ :(2k+1)  ;
; 
2) ( cos5x=cos( х-  ))
)) 


Ответ :  (8k+1);
(8k+1);  (8k-1).
(8k-1).
3) (cos x=sin3x)  (cos x=cos(
(cos x=cos(  -3x)
-3x) 


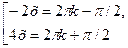
Ответ:  (4k+1);
(4k+1);  (4k+1).
(4k+1).
4) (5х-х = πk)  (4х = πk)
(4х = πk)  (х=πk/4).
(х=πk/4).
Из множества решений надо исключить те значения аргумента х, при которых левая и правая части уравнения не существуют, т. е. значения вида π/2(2k+1). В множестве х= π k/4=( π /2)-(к/2) такие значения получаются, если к/2—нечетное число:k/2 = 2n+ l, т.е. k = 4 π + 2. Следовательно, уравнению удовлетворяет множество корней вида π к/4 при к≠4n+2.
Контрольные задания
Вариант 1
1. Вычислите значения остальных трех тригонометрических функций, если
sinα= -5/13 и 3π/2<α<2 π; 2) cos α= - 8/17 и π /2<α< π; 3) tgα = 8/15 и π <α<Зл/2;
4) ctgα= - 7/24 и З π /2<α<2 π.
Упростите выражения:
sin2α + tg2α+cos2α; 2) sin4α — cos4α + cos2α;
3)  +
+  ; 4)
; 4)  +
+ 
5) tg2α cos2 α +ctg2α sin2 α; 6) cos4х + sin2х cos2x+sin2х; 7)  ;
;
8) sin α cos α (tg α +ctg α).
2.Докажите тождества:
1)  +
+  = sin x + cos x ;
= sin x + cos x ;
2) tg2α - sin2α = sin2α tg2α;
3) sin3α( l+ctg α)+cos α (l +tg α) = sin α +cos α;
4) 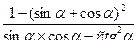 = 2tg2 α; 5)
= 2tg2 α; 5)  = sin2 α;
= sin2 α;
6) 1-sin6z-cos6 z =3sin2z cos2z;
7) cos2α (1 – tg α) (1 + tg α)=cos4 α - sin4 α.
3.Вычислите:
y =  , если tg х = 3;
, если tg х = 3;
у= 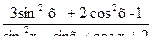 если tg х = 1;
если tg х = 1;
4.Упростите выражения:
1) (sin α+cos α)2+(sin α - cos α)2; 2) sin2 α + cos4 α - sin4 α;
3) sin4 α + sin2α cos2α + cos2 α; 4) ctg2 α - cos2 α ctg2 α - cos2 α;
5) 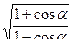 -
-  ; 6) ( l+sin α)(tg α + ctg α)( l- sin α);
; 6) ( l+sin α)(tg α + ctg α)( l- sin α);
7) ( l+tg α)2 + ( l - tg α)2; 8) tg α -  .
.
5. Докажите тождества:
(ctg α +l)2 + (ctg α -l)2 = 2 / sin2 α;
cos α +sin α tg α –l / cos α = 0;
tg2 α (1 + tg2 α) (1 + ctg2 α) - (1 - tg2 α)2= 4 tg2 α;
cos α (sin α +cos α) (1 - tg α) = cos4 α - sin4 α;
5)  =
=  ;
;
6) sin2 α sin2 β + sin2 α cos2 β +cos2 α = 1.
6. Вычислите значения выражений, если tgz = 2:
sin4z+cos4z; 2) sin6z+cos6z;
3)  ; 4)
; 4) 
7.Дано: tg α +ctg α =3. Найдите: 1) tg α -ctg α; 2) tg2 α -ctg2 α; 3) tg2 α +ctg2 α;
4) tg3 α +ctg3 α.
Вариант 2
1. Вычислите: 1) cos 7230°; 2) sin 900°; 3) tg585°; 4) ctg 750°;
5) sin 1843°.
2. Вычислите: 1) sin6,2 π +cos4,l π; 2) tg(13 π /4)+ctg(2l π /4);
3) sin(19 π /3)-сов(19 π /3); 4) sin(82 π -0,192)+cos(22 π +1,501);
5) sin 7,854-tg 3,927.
3. Найдите периоды функций: 1) y=cos3x; 2) y=cos(x/4);
3) y=tg2x; 4) y=ctg(x/5).
4. Найдите периоды функций: 1) у = sin 5x - cos4x +1; 2) у =2sin(x/4) - 3sin(x/3); 3) y=tg(2x/3) - 4ctg(3x/2) - 2; 4) у = sin (3х/4) - 3 cos (5х/8) + cos 5x.
5. Вычислите: 1) 2sin750° -3cos900° + tg405°; 2) tg2600° + ctg2585° + 3;
3) sin(-330°) +sin(-690 °); 4) tg(-135°) - tg225° ; 5) cos (-3π) - sin (-7 π);
6) 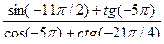
6. Упростите выражения:
1) sin2(6 π -α) + sin2(10 π + α); 2) sin2 (  - 4 π )+cos2 (8 π -
- 4 π )+cos2 (8 π -  ) + 2:
) + 2:
3) cos(α -6 π)+cos(12π + α); 4) sin2(2π+ α) + cos2 (6π - α) + 1.
7. Докажите тождества:
1)  ; 2)
; 2) 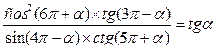 ; 3)
; 3) 
4) sin(6π -х) соs (8π –х) tg (9π -x) ctg (10π -х) = - sin x cos x.
Вариант 3
1. Проверьте, справедливы ли равенства: 1) arcsin (  /2) = π /4;
/2) = π /4;
2) arcsin (-1/2)= - π /6; 3) arccos (  /2)= π /6; 4) arccos (
/2)= π /6; 4) arccos (  /2)=З π /4;
/2)=З π /4;
5) arctg 1= π /4; 6) arctg  = π /3; 7) arctg (-
= π /3; 7) arctg (-  /3) = π /6; 8) arcctg
/3) = π /6; 8) arcctg  = - 2 π/3.
= - 2 π/3.
2. Вычислите: 1) arcsin 0,4067; 2) arcsin 0,9962; 3) arccos 0,9848;
4) arccos 0,1736; 5) arctg 0,2679; 6) arctg 2,747; 7) arcctg 2,145; 8) arcctg 0,1944.
3. Вычислите: 1) arcsin (-  /2); 2) arccos (- 1 /2); 3) arctg (-
/2); 2) arccos (- 1 /2); 3) arctg (-  /3); 4) arcctg(- 1);
/3); 4) arcctg(- 1);
5) arcctg(-  ); 6) arcsin ( 0,9033); 7) arccos(- 0,8965); 8) arctg (- 1,4659);
); 6) arcsin ( 0,9033); 7) arccos(- 0,8965); 8) arctg (- 1,4659);
9) arcctg (-1,3663); 10) arcctg (-0,3096).
4. Докажите справедливость неравенств: 1) arcsin(1/2)< arccos(l/2):
2) arccos 0> arcsin 0; 3) arcsin (1/4) > arcsin (1/6);
4) arctg  > arcctg
> arcctg  .
.
5. Вычислите: 1) arcsin (  /2) + arccos(
/2) + arccos(  /2); 2) arcsin (-1/2) + arccos (-1/2);
/2); 2) arcsin (-1/2) + arccos (-1/2);
3) arctg (-1) + arcctg (-1); 4) arcsin 1 + arccos 1 + + arctg 1 + arcctg 1;
5) arcsin (- 1) + arccos (-1); 6) arcsin 0 + arccos 0; 7) arcsin 0 + arcsin 1+arcsin ( - 1); 8) arccos 0 +arccos 1 + arccos (- 1).
Вычислите:
6. 1) cos 150°; 2) tg135°; 3) sin 120°; 4) ctg 130°; 5) cos 210°; 6) sin 260°; 7) tg 220°;
8) ctg 200°; 9) sin 210°; 10) sin 350°; 11) cos 280° ; 12) tg 340°; 13) ctg 325°; 14) sin 345°;
15) cos 295°; 16) tg 335°.
7. 1) cos 225°; 2) sin 150°; 3) ctg210°; 4) tg 225°; 5) cos 315°; 6) tg l20°; 7) ctg 150°;
8) sin 220°; 9) cos 230°; 10) tg 250°; 11) sin 315° ; 12) cos 340°.
8. 1) sin 3,52; 2) cos 3,68; 3) ctg 5,11.
9. Вычислите:
1) sin 9135°+cos(- 585°)+tg 1395°+ctg(- 630°);
2) sin(-810) +cos(-900°)+tg(-395°)ctg575°;
3) sin(-2383o)-sin(-2023°)+cos(- 485o)-cos(-125°);
4) 3 tg 930°+sin l200°-cos l410°;
5) cos 510°- sin 480°+cos 840° +sin 1230°;
6) sin (- 1Зπ/6)+cos (17π/3)+tg (22π/3) - ctg (37π/4);
7) sin (- 47π/3) - tg (21 π/4)+tg( - 23π/4) - ctg (19π/6).
10. Упростите:
1) sin (α - Зπ/2) cos (2π - α) - sin (π - α) sin (π+ α);
2) 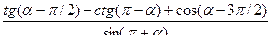
11. Докажите тождества:
1)  +
+ 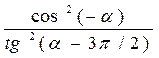 =1;
=1;
2)  =sin α
=sin α
3)  = - 1
= - 1
Вариант 4
Решите уравнения:
1) cos2(π - x) + 8cos(π + x) + 7 = 0;
2) 2cos2(x - π)+3sin(π + x)=0;
3) 2 sin2 х+5 sin (3 π /2 - х)- 2=0;
4) 5 cos2(х - 3π/2)- 2cos(х- π/2) = 0;
5) 3sin 2(х-3π/2) - cos (х+4π) = 0;
6) 5tg2(х - π)+12tg(π -x)=0;
7) 2tg2(3π /2+x) + 3tg(π /2 + х)=0.
Вариант 5
1. Вычислите, не применяя таблиц, значения синуса и косинуса дуг
 ,
, 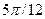 и
и  ;
;  ,
,  .
.
Вычислите:
2. 1) sin  и sin
и sin  если cos
если cos  =4/5, sin
=4/5, sin  =-3/5, З
=-3/5, З  /2<
/2<  <2
<2  ,
,  ; 2) cos
; 2) cos  и cos
и cos  ,если sin
,если sin  =8/17 и cos
=8/17 и cos  =3/5,
=3/5,  /2<
/2<  <
<  и З
и З  /2<
/2<  <2
<2  . 3) sin (
. 3) sin (  /4+
/4+  ) и cos(
) и cos(  /4+
/4+  ), если tg
), если tg  =-3/4,
=-3/4,  /2<
/2<  <
<  .
.
3. cos (arccos (1/7)-arccos (11/14)); 2) sin (arcsin (5/13)+arcsin (12/13)); 3) tg (arctg (2/3)-arctg (1/3)); 4) ctg(arcctg5-arcctg(l/5)).
4.  ;2).
;2).  3).
3).  ;4).
;4).  ;
;
5) ctg(  ;если sin
;если sin  := -1/2 и
:= -1/2 и  <
<  <3
<3  /2
/2
5. Упростите:
1) cos (  /4) cos (
/4) cos (  /6) -sin (
/6) -sin (  /4) sin (
/4) sin (  /6); 2) sin (
/6); 2) sin (  /3) cos (
/3) cos (  /4)-cos (
/4)-cos (  /3) sin (
/3) sin (  /4);
/4);
3) sin(  +
+  )-sin(
)-sin(  -
-  ); 4) cos (
); 4) cos (  /3 +
/3 +  ) cos (
) cos (  /3-
/3-  ) - cos2
) - cos2  ; 5) 2 sin (
; 5) 2 sin (  /4+
/4+  ) sin (
) sin (  /4-
/4-  )+sin2
)+sin2  ; 6) sin 2
; 6) sin 2  - cos 2
- cos 2  tg
tg  ; 7).
; 7). 
6. Докажите тождества:
1) sin (  +
+  ) sin (
) sin (  -
-  )=sin2
)=sin2  - sin2
- sin2  ;
;
2) cos (  +
+  ) cos (
) cos (  -
-  )=cos2
)=cos2  -sin2
-sin2  ;
;
3). 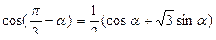 ;
;
4). 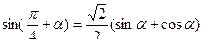
7. Решите уравнения: 1) sin2xcosx=cos2хsinx; 2) 8 sin x(  /6-х) - 3cosx=0; 3) 5sin(
/6-х) - 3cosx=0; 3) 5sin(  /3+х) + 7sin(
/3+х) + 7sin(  /3-x)=0.
/3-x)=0.
Вычислите:
8. 1) cos(  +
+ 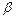 ) и cos(
) и cos(  -
- 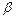 ), если cos
), если cos  =3/5 и cos
=3/5 и cos 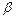 =7/25, 0<
=7/25, 0<  <
<  /2 и 0<
/2 и 0< 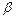 <
<  /2; 2) sin(
/2; 2) sin(  -
- 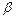 ) и cos (
) и cos (  -
- 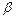 ), если sin
), если sin  = -4/5 и cos
= -4/5 и cos 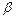 = -24/25,
= -24/25,  <
<  <3
<3  /2,
/2,  <
< 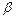 <3
<3  /2.
/2.
9. 1) tg(  -45°), если ctg
-45°), если ctg  = 2/3; 2) ctg(
= 2/3; 2) ctg(  -45°), если tg
-45°), если tg  =3/2.
=3/2.
10. Упростите: 1) sin (  /12)+cos (
/12)+cos (  /12); 2) sin2(
/12); 2) sin2(  -
- 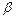 )+sin2
)+sin2 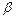 + 2 sin (
+ 2 sin (  -
- 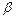 )cos
)cos  sin
sin 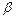 .
.
Докажите тождества:
11. 1) sin (  /6 +
/6 +  )+sin (
)+sin (  /6 -
/6 -  ) = cos
) = cos  ;
;
2) cos2  +cos2 (
+cos2 (  /3+
/3+  )+cos2 (
)+cos2 (  /3 -
/3 -  ) = 3/2;
) = 3/2;
3).  =tg(
=tg(  /4+
/4+  );
);
4). 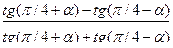 =2sin
=2sin  cos
cos  ;
;
12. 1).  =
=  ;
;
2).  -1=
-1= 
3). 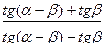 =
=  ;
;
4) (tg  + tg
+ tg 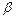 ) ctg (
) ctg (  +
+ 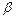 )+(tg
)+(tg  - tg
- tg 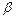 ) ctg (
) ctg (  -
- 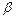 ) = 2;
) = 2;
5).  +
+ 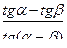 =2.
=2.
13 1) sin(  +
+  +
+  )=sin(
)=sin(  +
+  )cos
)cos  +cos(
+cos(  +
+  )sin
)sin 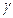 ;
;
2) cos (  +
+  +
+  )=cos (
)=cos (  +
+  )cos
)cos  - sin(
- sin(  +
+  ) sin
) sin 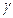 ;
;
3).  +
+  +
+  =0.
=0.
14. 1) cos 15° +  sin 15° =
sin 15° =  .
.
2) cos 59° cos 79°+cos 31° cos 11° +cos 20° = 2 cos 20°;
3).  =tg25°;
=tg25°;
4).  =
=  .
.
15. Решите уравнения:
1)cos 2x cos x = sin 2x sin x;
2) 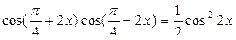 ;
;
3) 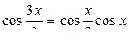 .
.
Вариант 6
Вычислите:
1. sin2  , cos2
, cos2  и tg2
и tg2  , если: 1) sin
, если: 1) sin  = -3/5 и
= -3/5 и  <
<  <3
<3  /2;
/2;
2) cos  =5/13 и 3
=5/13 и 3  /2<
/2<  <2
<2  ; 3) tg
; 3) tg  = -3/4 и
= -3/4 и  /2<
/2<  <
<  .
.
2. 1) ctgz, если tg(z/2)=5/3; 2) sin 3  , cos 3
, cos 3  и tg3
и tg3  , если sin (3
, если sin (3  /2) = -5/13 и
/2) = -5/13 и  <3
<3  /2; 3) cos4x и tg4x, если tg x = 1/5 и
/2; 3) cos4x и tg4x, если tg x = 1/5 и  <х<3
<х<3  /2.
/2.
3. Найдите числовые значения выражений: 1) sin2  /(2cos
/(2cos  ), если cos
), если cos  = -4/5 и
= -4/5 и  <
<  <3
<3  /2; 2) cos2
/2; 2) cos2  /sin
/sin  , если sin
, если sin  = -3/5 и 3
= -3/5 и 3  /2<
/2<  <2
<2  .
.
4. Выразите: 1) sin4  через sin
через sin  и cos
и cos  ; 2) cos4
; 2) cos4  через sin
через sin  и cos
и cos  ; 3) tg3
; 3) tg3  через tg
через tg  ; 4) cos4
; 4) cos4  через cos
через cos  ; 5) sin5
; 5) sin5  через sin
через sin  .
.
5. Упростите: 1).  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
6. Докажите тождества:
1) 2sin2  +cos2
+cos2  =l; 2) 1 + cos2
=l; 2) 1 + cos2  =2cos2
=2cos2  ;
;
3).  =ctg2
=ctg2  ; 4).
; 4).  =tg
=tg 
5) cos4  +sin4
+sin4  = 1-0,5 sin2 2
= 1-0,5 sin2 2  ;
;
6) cos6  +sin6
+sin6  = 1 - 0,75 sin2 2
= 1 - 0,75 sin2 2  ;
;
7).  =
=  ; 8).
; 8).  =сtg
=сtg  ;
;
9).  =tg
=tg  ; 10).
; 10).  =tg2
=tg2  ;
;
11).  -
-  =2; 12).
=2; 12).  .
.  =сtg
=сtg  ;
;
13) cos 4  +4cos2
+4cos2  +3 = 8cos4
+3 = 8cos4  .
.
7. Решите уравнения:
1) sin2x—sinx=0; 2) sinxcosx: = 1/2; 3) cos2x—sin2x = l.
Вариант 7
1. Упростить: 1)  ; 2)
; 2) 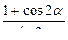 .
.
2). 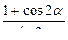 =
=  =
=  =ctg
=ctg 

Вычислите: sin (  /2), cos (
/2), cos (  /2) и tg(
/2) и tg(  /2), если: 1) cos
/2), если: 1) cos  = -7/25 и
= -7/25 и  /2<
/2<  <
<  ; 2) sin
; 2) sin  = -15/17 и 3
= -15/17 и 3  /2<
/2<  <2
<2  ; 3) tg
; 3) tg  =4/3 и 0<
=4/3 и 0<  <
<  /2.
/2.
2. 1) cos (  /2), если tg
/2), если tg  = - 12/5 и 5
= - 12/5 и 5  /2<
/2<  <3
<3  ; 2) sin (
; 2) sin (  /2), если ctg
/2), если ctg  = 5/12 и 3
= 5/12 и 3  <
<  <7
<7  /2.
/2.
3. 1) sin  , если ctg (
, если ctg (  /2) = 1/3; 2) cos
/2) = 1/3; 2) cos  , если ctg (
, если ctg (  /2) = 1/2; 3) tg
/2) = 1/2; 3) tg  ,
,
если ctg(  /2)=
/2)=  3/3; 4)
3/3; 4) 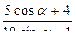 , если tg(
, если tg(  /2)=2.
/2)=2.
4. Решите уравнения: 1) 1—cosх = sin(x/2); 2) l+cosx: = = cos(x/2); 3) 1+cosx=sinx.
Вычислите:
5. 1) sin2a  , cos2
, cos2  и tg2
и tg2  , если sin
, если sin  =4/5 и 0<
=4/5 и 0<  <
<  /2; 2) sin (
/2; 2) sin (  /2), cos (
/2), cos (  /2) и tg(
/2) и tg(  /2), если cos
/2), если cos  = 1/2 и 0<
= 1/2 и 0<  <
<  /2; 3) sin (
/2; 3) sin (  /4), cos (
/4), cos (  /4) и tg(
/4) и tg(  /4), если sin
/4), если sin  = -24/25 и 3
= -24/25 и 3  /2<
/2<  <2
<2  .
.
6. 1).  2).
2). 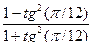 3).
3). 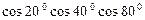
7. 1) sin (2 arcsin (40/41)); 2) cos (2 arccos (2/3)); 3) tg(2 arctg(7/25)).
Упростите:
8 1) l-cos40°; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5) tg  (l+cos2
(l+cos2  ); 6)
); 6) 
9. 1).  2).
2).  3).
3). 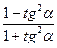
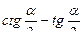
Преобразуйте в алгебраическую сумму:
10
1)cos7x cos5x; 2) sin 11x sinx; 3) sin5x cos2x;
4) sin(  -
-  )cos(
)cos(  +
+  ); 5) cos(
); 5) cos(  +
+  )cos(2
)cos(2  +
+  );
);
cos 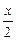 cos
cos 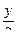 cos
cos 
11. 1)sin(  +x) sin(
+x) sin(  -x )2) 4cos(
-x )2) 4cos(  -x) cos(
-x) cos(  +x);
+x);
3)4cos(  -x) cos(
-x) cos(  -x) 4). 4cos(
-x) 4). 4cos(  +x) sin(
+x) sin(  -x)
-x)
12. Представьте в виде сумм первых степеней: 1) cos3x; 2) sin4x; 3) cos4x; 4) sin5x; 5) cos5x.
Вариант 8
Преобразуйте в произведение:
1. 1) cos(π /3)-cos(2 π /3); 2) cos β- sin α; 3) 2 cos2 α -sin 2 α;
4) cos20° +sin50°; 5) tg25°-ctg75°; 6) sin2 5 α -sin2З α.
2. 1) sin α cos β +2sin2(α /2)sin β; 2) sin 10°+ 2 sin 5° cos 15° + +cos 50°.
3. 1) sin 16°+sin26° -sin42°; 2) sinA + sin B+sin(A+ B)/2;
3) sin(α /2)-sin(3 α /2)+cos α; 4) sin A+cos B+cos C, где A + B+C= π
5) sin 25° + sin 37°+sin 27° + sin 35°.
4. Покажите, что для углов А, В и С всякого треугольника имеют место соотношения:
1) sin A + sin B-sin C=4sin  sin
sin 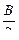 cos
cos  ;
;
2) 1- cos A+cos B+cos C=4sin  cos
cos 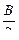 cos
cos  ;
;
3)  ctg
ctg  ctg
ctg 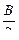 ;
;
4) tg A + tg B+tg C=tg A tg B tg C.
5Докажите тождества:
1) 1 +sin α +cos α =4cos  sin
sin  cos(
cos(  -
-  )
)
2) sin α +cos α-1=2  sin
sin  cos(
cos(  +
+  )
)
3) 2 cos2 α +cos α -1 = 2 cos (3 α /2) cos (α /2).
6. Решите уравнения:
1) sin5x=cos(  -7x); 2) ctg(
-7x); 2) ctg(  -x)= - tg(
-x)= - tg(  -2x);
-2x);
3) cos(  -x)- cos(
-x)- cos(  +x)=0; 4) cos(x-70°)-sin(x+70°)=0
+x)=0; 4) cos(x-70°)-sin(x+70°)=0
7. Преобразуйте в суммы тригонометрических функций первой степени следующие произведения:
1) 4 cos  cos α sin
cos α sin  ; 2) 4 cos
; 2) 4 cos  cos α sin
cos α sin  ;
;
3) 4 cos  cos α cos
cos α cos  .
.
8 Упростите путем преобразования в суммы следующие произведения:
1) sin 20° sin 40° sin 60° sin 80°; 2) tg20otg40°tg60otg80°.
9. Преобразуйте в произведение:
1) sin α +sin 2 α +sin 4 α +sin 5 α; 2) sin З α + sin 2 α + 2 sin  cos
cos  .
.
10. Решите уравнения:
1) sin (х+  )cos(х-
)cos(х-  )= 1; 2) sin (х+
)= 1; 2) sin (х+  )cos(х-
)cos(х-  )= -
)= - 
Докажите тождества:
11. 1) sin2α cos α=(1/4)(cosα –соs3α)
2) sm3α cosα = (1 /8)(2 sinα 2 – sin4α)
3) sin2α cos3α =(1/6)(2 сos α –cos3α-cos5α),
4) sin3αcos3α =(1/32)(3sin2α-sin6α)
12. l) 4 sin α sin 2α sin 3α=sin 2α + sin4α-sin46α.
2) 4sinα sinβ cos(α-β)=cos2α+cos2β-cos2(α+β)-1
3) sin(  +α)sin(
+α)sin(  -α)cos2α=
-α)cos2α=  +
+  cos4α
cos4α
13. 1) 
2) 
3) 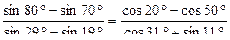
4) 
5) 
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить не менее семи заданий каждого из восьми предложенных вариантов, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 5
«Дифференциальное исчисление»
Цели:
– формирование навыков нахождения производной функции по формулам;
– формирование навыков вычисления производной функции в точке;
– формирование навыков решения физических задач с помощью производной;
– формирование навыков построения графиков функций, используя геометрический смысл производной
Дата добавления: 2019-01-14; просмотров: 985; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
