Примеры решения показательных и логарифмических уравнений и неравенств
1. Решить уравнение:
а) 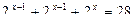 б)
б) 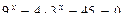
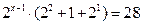
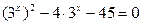
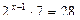
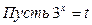
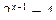
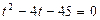
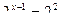

Функция y = 2t монотонна, значит 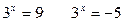
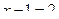
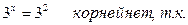
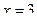

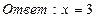
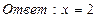
в) 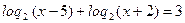
Область допустимых значений:
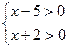
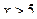
По свойству логарифма:
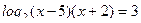
По определению логарифма:
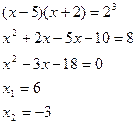
x 2 = -3 не удовлетворяет ОДЗ
Ответ. 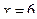
г) 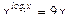
Область допустимых значений
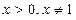
Прологарифмируем обе части уравнения по основанию 3:
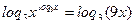
Применим свойства логарифма
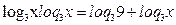
Пусть 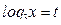
t2 = 2 + t
t2 – t – 2 = 0
t1 = 2 t2 = -1
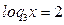
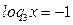
x1 = 32 x2 = 3-1
x1 = 9 x2 = 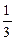
Ответ: x1 = 9, x2 = 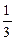 .
.
2.Решить неравенства:
а) 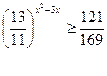
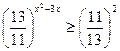
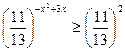
Т.к. 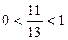 , то функция
, то функция 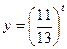 убывает:
убывает:
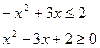

Решим неравенство методом интервалов:
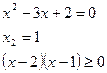

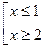
Ответ. 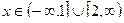

б)
|
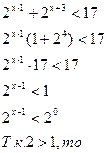

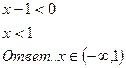
в) 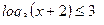

Область допустимых значений:
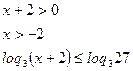
Т.к. 3>1, то функция y=loq3t возрастает:
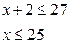
Таким образом, исходное неравенство равносильно системе неравенств:
|
|
|
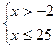
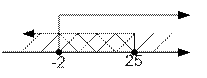
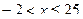
Ответ. 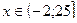
г) 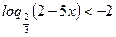
Область допустимых значений:
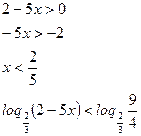
Т.к. 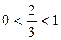 , то функция
, то функция 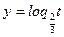 убывает:
убывает:
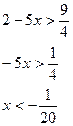
Таким образом, исходное неравенство равносильно системе неравенств:
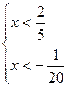
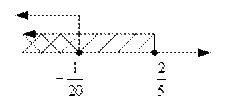
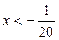
Ответ. 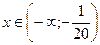
Контрольные задания
Вариант1
Найдите области определения функций:
7. 1) 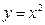 2)
2) 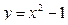 3)
3) 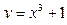
8 1) 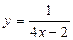 2)
2) 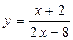 3)
3) 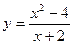
9 1) 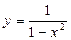 2)
2) 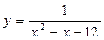 3)
3) 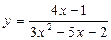 4)
4) 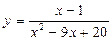
10 1) 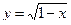 2)
2) 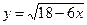 3)
3) 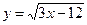
11 1) 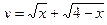 2)
2) 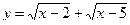
12 1) 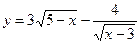 2)
2) 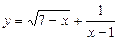
13 1) 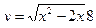 2)
2) 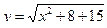 3)
3) 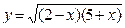
14 1) 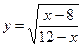 2)
2) 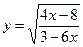
Вариант 2
1.Вычислите х:
1) 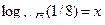 2)
2) 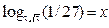
3) 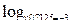 4)
4) 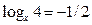
5) 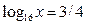 6)
6) 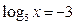
2. Найдите области определения функций:
1 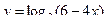 2)
2) 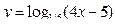
3) 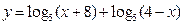
3. Постройте графики функций:
1) 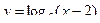 2)
2) 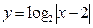 ; 3)
; 3) 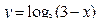
Вариант 3
1.Решить уравнения:
а) 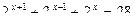
б) 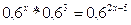
в) 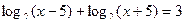
г) 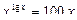
2.Решить неравенство:
а) 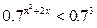
б) 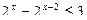
в) 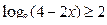
г) 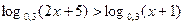
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить по три упражнения из каждого задагния во всех, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 4
«Тригонометрические функции»
Цели:
- формирование навыков выполнения тригонометрических преобразований;
|
|
|
- формирование навыков доказательства тригонометрических тождеств;
- формирование навыков решения тригонометрических уравнений и простейших тригонометрических неравенств
Тригонометрия
ЕДИНИЧНАЯ ЧИСЛОВАЯ ОКРУЖНОСТЬ
Окружность с центром в начале координат и радиусом, равным 1, называется единичной окружностью. Уравнение единичной окружности имеет вид
х2 + у2 = 1.  Точку А(1; 0) единичной окружности примем за начало отсчета дуг, а положительную полуось ОХ—за начальную
Точку А(1; 0) единичной окружности примем за начало отсчета дуг, а положительную полуось ОХ—за начальную
сторону центрального угла, образуемого
радиусом-вектором ОМ с осью ОХ
(точка М лежит на единичной окружности).
Вращение радиуса-вектора ОМ от
положительной полуоси ОХ против движения
часовой стрелки назовем положительным, а
дугу AM и центральный угол
/_ АОМ положительными; при противоположном
вращении (по часовой стрелке) = отрицательными.
Дуги I четверти заключены в промежутке 0< α <π/2, II четверти—в промежутке
π/2< α < π, III четверти — в промежутке π < α <З π /2 и IV четверти — в промежутке З π /2< α <2 π.
Существует бесконечное множество дуг, имеющих данное начало А иданный конец М(данные начальную и конечную стороны угла). Множество этихдуг (углов), как положительных, так и отрицательных, выражается формулой
|
|
|
α = 2πκ+ α1, или α =360°κ+α1, (1)
где 0≤ α,<2π (0≤ α <360 ) и kЄ Z.
Если каждому действительному числу α на единичной окружности соответствует точка Мαконец дуги AM, для которой дуга AM имеет величину α, то такая единичная окружность называется числовой единичной окружностью.
Длина всей числовой единичной окружности равна 2π. Если два числа отличаются друг от друга на целое кратное 2π, то на числовой единичной окружности им соответствует одна и та же точка. Если два числа соответствуют одной и той же точке числовой единичной окружности, то их разность кратна 2π.
1. Указать на единичной окружности: 1) точку М дуги АМ=17π; 2) точку М дуги АМ= 1950°; 3) точку М дуги АМ = -1380°.
1) Но формуле (9.11) получим 17 π = 16 π + π = 2 π -8 + π. k = 8. Конец дуги AM оканчивается в точке М (-1:0).
2) Находим АМ= 1950°=360° ∙ 5+ 150°, k = 5. Конец дуги AM оканчивается во II
четверти.
3) Имеем AM = - 1380° =360° ∙ (-4) +60°, k = - 4. Конец дуги AM
оканчивается в I четверти. Здесь дуга α1, представлена наименьшим по абсолютной величине числом (α1, =60°). Чтобы α1, было наименьшим по абсолютной величине числом, его надо брать в промежутке 0 ≤α1 < 180° или -180°< α1≤0.
|
|
|
2. Записать в общем виде концы дуг единичной окружности: 1) абсциссы которых равны нулю; 2) ординаты которых равны нулю.
1) Концы дуг π /2 и З π /2 ( — π /2) имеют абсциссы, равные нулю; следовательно, множество концов дут с абсциссой, равной нулю, записывается в виде π /2+ πk, kЄ Z.
2) Концы дуг 0 (2π) и π имеют ординаты, равные нулю; следовательно, множество концов дуг с ординатой, равной нулю, записывается в виде πk , kЄ Z.
3. Укажите, в какой четверти единичной окружности оканчиваются дуги: 1) 120°;
2) 315° ; 3) -220° : 4) 850°; 5) 500°; 6) -120; 7) π /4; 8) 7 π /6; 9) -5 π /3: 10) 4 π /15;
11) 8 π /3; 12) -5 π /4; 13) 0,76; 14) 5,8; 15) -7,2; 16) -3,7: 17) 15; 18) 3,3.
4. Представьте угол α по формуле (1), взяв наименьший из абсолютной величине угол α1, если: 1) α = 2200°; 2) α 550; 3) α = -740°; 4) α = 1170° ;5) α = -1450°;
6) α=520°,
5. Запишите в общем виде дуги, оканчивающиеся в точках:
1) А(1; 0); 2) В (0; 1): 3) С(-1;0); 4) D(0; -1).
6. Единичная окружность разделена на 12 равных частей, начиная от точки
А (1; 0). Запишите множества концов дуг, оканчивающихся в точках деления.
7. Найдите значения дуг: 1) πк; 2) π/4+2πk; 3) π/3 + 2πk; 4) (-1)к п/6 + пк при
k = - 2; -1; 0; 1; 2.
8. На единичной окружности отметьте дуги α, удовлетворяющие условиям:
1) 0< α <π/4; 2) π/4< α <π/3; 3) -π/6< α <π/6; 4) -2π/3< α <0; 5) | α |≤ π /3; 6) | α |≤ π/2.
9. На единичной окружности: 1) постройте точки, соответствующие числам π/6; π/4; π/3; 2π/3; - 2π/3; - Зπ/4;
2) постройте приближенно точки, соответствующие числам 1,5; 3,5; 5; 6; -2; -4.
10. Точка единичной окружности, лежащая в конце дуги π/6, начала равномерное движение по окружности в положительном направлении со скоростью
ω = 4π/3 рад/с. В какой четверти окажется точка через: 1) 2 с; 2) 3 с; 3) 4 с; 4) 10 с?
11. Напишите общий вид дуг α, если: 1) 2 α = π /4 + 2 π k;
2) З α - π /6 = 5 π /6 + 2 π k; 3) 4 α + π /3 = 2 π /3 + π k; 4) 10°+ α =50°+180°k.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЧИСЛОВОГО АРГУМЕНТА
Абсцисса X точки М, числовой единичной окружности (рис. 38) Y
 называется косинусом числа α:
называется косинусом числа α:
X=cos α. (2)
Ордината Y точки Ma чистовой единичной
окружности называется синусом числа α:
Y = sin α. (3)
Областью определения косинуса и синуса
служит множество всех действительных чисел,
т. е. D (cos α) = R, D(sin α)=R.
Отношение синуса числа α к его косинусу
называется тангенсом числа α:
tg α = sin α /cos α. (4)
Область определения тангенса — множество всех действительных чисел, за исключением чисел вида π /2+ π k, kЄ Z..
Отношение косинуса числа α к его синусу называется котангенсом числа α:
ctg α =cos α /sin α. (5)
Область определения котангенса — множество всех действительных чисел, за исключением чисел вила πk. kЄ Z.
Величина, обратная косинусу числа α, называется секансом числа α:
sec α =l/cos α. (6)
Область определения секанса - множество всех действительных чисел, за исключением чисел вида π/2 + πk. kЄ Z.
Величина, обратная синусу числа α, называется косекансом числа α:
cosec α = 1/sin α. (7)
Область определения косеканса — множество всех действительных чисел, за исключением чисел вида πk, kЄ Z.
При решении задач тригонометрические функции рассматриваются или как функции числа, или как функции дуги (угла), заданные на множестве всех действительных чисел или на множестве всех дуг (углов). При этом каждому действительному числу или каждой дуге (углу) соответствует единственное значение тригонометрической функции.
Функции cos α и sin α ограничены, так как -1 ≤ Е (cos α) ≤ 1 и -l≤ Е (sin α) ≤1.
Функции tg α и ctg α не ограничены, так как каждая из них может принимать любое действительное значение, т.е. E(tg α)=R и Е(ctg α) = R.
1. Могут ли синус и косинус быть равными: 1) 0,85; 2) 7/6;
3) - 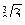 /
/ 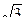 ; 4) -1,01; 5) 3/
; 4) -1,01; 5) 3/ 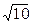 ; 6)
; 6) 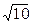 /π; 7) α /
/π; 7) α / 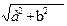 , α >0, b>0; 8) α /
, α >0, b>0; 8) α / 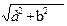 , а>0,
, а>0, 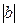 <а?
<а?
2. Могут ли синус, косинус, тангенс и котангенс принимать значение, равное:
1/2; 2) 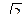 ; 3) -5,1; 4)
; 3) -5,1; 4) 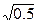 ; 5) 2,2; 6)
; 5) 2,2; 6) 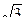 /2?
/2?
3. Могут ли функции sin α, cos α, tg α, ctg α принимать отрицательные значения, если α выражает величину угла треугольника?
4. Чем отличаются друг от друга области определения sin α и tg α?
5. Сравните абсолютную величину тангенса любого числа с абсолютной величиной синуса этого числа.
6. Какие множества значений имеют функции sin α, cos α, tg α и ctg α?
7. Найдите значения а в промежутке 0≤ α ≤2π, для которых выполняется равенство:
1) sin α =0; 2) sin α =l; 3) sin α = — 1; 4) cos α =0; 5) cos α =l; 6) cos α = — 1.
8. Найдите значения a в промежутке 0≤ α ≤2π, для которых выполняется равенство:
1) tg α =0; 2) tg α = 1; 3) tg α = - 1; 4) ctg α =0, 5) ctg α =l; 6) ctg α = - 1.
Дата добавления: 2019-01-14; просмотров: 495; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

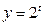 возрастает:
возрастает: