ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ.
Любое тригонометрическое уравнение приводится к простейшему:
| Sin X = a 1) ׀a׀> 1 уравнение не имеет решений 2) 0 = ׀a׀ sin X = 0 X = πn, n Є Z 3) a = 1 sin X = 1 X = π/2 + 2 πn, n Є Z 4) a = -1, sin X = -1 X = -π/2 + 2 πn, n € Z 5) ׀a׀ < 1, a ≠ 0 X = (-1)n arcsin a +πn, n Є Z | Cos X = a 1) ׀a׀ > -1 уравнение не имеет решений. 2) 0 = ׀a׀ cos X = 0 X = π/2 + πn, n Є Z 3) а =1 cos X = 1 X = 2 πn, n Є Z 4) a= -1 cos X = -1 X = π + 2 πn, n Є Z 5) ׀a׀ < 1, a ≠ 0 cos X = a X = ± arccos a + 2 πn, n Є Z |
| Tg X = a X = arctg a + πn, n Є Z | Ctg X = a X = arcctg a + πn, n Є Z |
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРАИЧЕСКОЙ СУММЫ ДВУХ АРГУМЕНТОВ (ФОРМУЛЫ СЛОЖЕНИЯ)
Для нахождения тригонометрических функций суммы и разности двух аргументов применяются следующие формулы:
sin(α+β)=sin α cos β +cos α sin β; (20)
sin (α-β)=sin α cos β -cos α sin β; (21)
cos(α+β)=cos α cos β -sin α sin β; (22)
cos(α-β)=cos α cos β + sin α sin β; (23)
tg(α+β) = 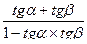 , α≠
, α≠  (2k+1), β ≠
(2k+1), β ≠  (2k+1),
(2k+1), 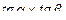 ≠1; (24)
≠1; (24)
tg(α-β)= 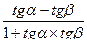 , α≠
, α≠  (2k+1), β ≠
(2k+1), β ≠  (2k+1),
(2k+1), 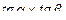 ≠1.
≠1.
(25)
|
|
|
сtg(α+β)= 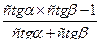 , α≠ πk, β≠ πk, α≠ - β+ πk (26)
, α≠ πk, β≠ πk, α≠ - β+ πk (26)
сtg(α-β)= 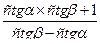 , α≠ πk, β≠ πk, α≠ β+ πk (27)
, α≠ πk, β≠ πk, α≠ β+ πk (27)
Вычислить:
1. 1) sin(α+β), если sin α =3/5, cos β = - 5/13, π/2< α <π, π< β <3π/2; 2) sin(α-β), если cos α = - 4/5, sin β = - 24/25, π< α <3π/2, 3π/2< β <2π ; 3) cos(α+β), если tg α = - 24/7,
tg β = 15/8, π/2< α <π, π< β <3π/2.
1) Найдем cos α и sin β при условии π/2< α <π, π< β <3π/2; cos α = - 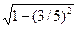 =
=
= - 4/5, sin β = - 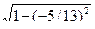 = - 12/13. По формуле (9.34) получим
= - 12/13. По формуле (9.34) получим
sin(α+β)=(3/5)(-5/13)+(- 4/5)(-12/13) = 33/65.
2) Находим sin α = -  = -3/5; cos β =
= -3/5; cos β = 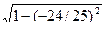 =7/25. По формуле получим
=7/25. По формуле получим
sin (α- β)=(- 3/5) (7/25) - (- 4/5) • (- 24/25) = -117/125.
3) Из формулы l+tg2 α =l/cos2 α имеем cos α =± l/  . Учитываем, что π/2< α <π,_находим
. Учитываем, что π/2< α <π,_находим
cos α = -1/ 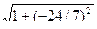 = -7/25, sin α =
= -7/25, sin α = 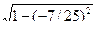 = 24/25.
= 24/25.
Аналогично находим cos β = - 8/17 и sin β = —15/17. По формулам (9.36) получаем
cos(α+ β)=(-7/25) (- 8/17) - (24/25)(-15/17)=416/425.
2. 1) sin (arcsin (3/5)+arcsin (4/5)); 2) cos (arccos (3/5)+arcsin (8/17)).
1) Обозначив arcsin (3/5)= α и arcsin (4/5) = β, имеем sin α =3/5,
|
|
|
- π /2≤ α ≤π /2 и sin β= 4/5, -π /2≤ β ≤π /2. Находим cos α =  =4/5 и
=4/5 и
cos β = 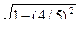 = 3/5. Следовательно,
= 3/5. Следовательно,
sin (arcsin (3/5)+arcsin (4/5)) = sin (α+β) = sin α cos β +cos α sin β =
=(3/5)(3/5)+(4/5)(4/5) = l.
2) Обозначив arccos (3/5)= α и arcsin (8/17) = β, имеем cos α = 3/5, 0≤ α ≤π и
sin β = 8/17, - π/2≤ β ≤π/2 . Находим sina α=  =4/5 и
=4/5 и
cos β = 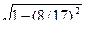 == 15/17. Таким образом,
== 15/17. Таким образом,
cos (arccos (3/5)+arcsin (8/17))=cos (α+β) =cos α cos β -sin α sin β =
=(3/5)-(15/17)-(4/5)(8/17)= 13/85.
3. 1) sin 20° cos 40° +cos 20° sin 40°; 2) cos 47° cos 17° + sin 47° sin 17°.
1) sin 20°cos 40°+cos 20°sin 40° = sin(20°+40°) = sin60°= 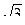 /2 ;
/2 ;
2) cos 47o cos l7o + sin 47o sin l7°=cos(47o-17o) = cos 30° = 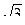 /2.
/2.
4. 1) tg(α+β), если tg α = 1/5, tg β =2/3; 2) ctg(α-β), если tg α =3/2, tg β = 5/2;
3) tg(π/4+α), если sin α = 12/13, π/2< α <π.
1) получим
tg(α+β)= 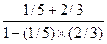 =1
=1
2) Находим ctg α =l/tg α =2/3, ctg β = 1/tg β = 2/5. По формуле получим
сtg(α-β)= 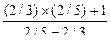 = -
= - 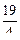
3) Имеем
tg( 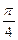 +α)=
+α)=  =
= 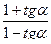
По формуле tga α = 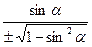 находим tg α = -
находим tg α = - 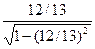 = -
= - 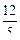
Подставив найденное значение тангенса, получим
Tg( 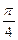 +α)=
+α)= 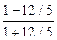 = -
= - 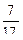
5.1) tg(arctg(l/2)+arctg(3/2)); 2) ctg (arcsin (4/5)+arctg 3).
1) По формуле получим
tg (arctg (1 /2)+ arctg (3/2))= 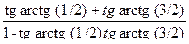
|
|
|
2) Обозначив arcsin (4/5)= α и arctg 3 = β, получим sin α =4/5, - π/2≤ α ≤π/2 и tg β =3,
- π/2< β <π /2. Далее, находим ctg α =3/4; ctg β =1/3. По формуле (9.40) получим
ctg(arcsin(4/5)+arctg 3)=ctg(α + β)=  = -
= - 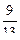
6. Упростить: 1) sin α cos 2 α +cos α sin 2 α; 2) 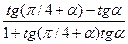
1) Используя формулу, получим
sin α cos 2 α +cos α sin 2 α = sin (α + 2 α) = sin 3 α.
2) Используя формулу (9.39), получим
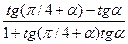 =
= 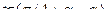 =
= 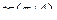 =1.
=1.
7. Доказать тождества:
1). 

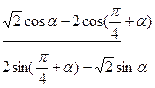 =tg
=tg  ; 2).
; 2). 
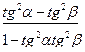 =
= 
1) Упрощая левую часть равенства, получим
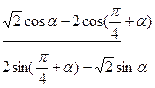 =
= 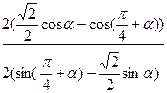 =
=
= 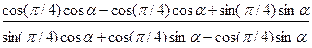 =
=  =tg
=tg  ,
,
т. е. тождество доказано.
2) Упрощаем правую часть равенства:
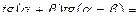
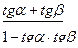
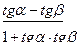 =
= 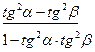
8. Решить уравнения:
1) sin2xcosx+cos2xsinx=0;
2).  ; 3).
; 3). 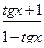 =1
=1
1) Используя формулу (9.34), получим
(sin 2х cos х+cos 2 x sin x=0)ó(sin (2 x+ x)=0)ó(sin 3х +0)ó(  ) ó
) ó  k/3.
k/3.
2) sin (  /4) cos х+cos (
/4) cos х+cos (  /4) sin х+cos х cos (
/4) sin х+cos х cos (  /4)+sin х sin (
/4)+sin х sin (  /4)=0.
/4)=0.
Сократив на sin (  /4) [sin (
/4) [sin (  /4)=cos (
/4)=cos (  /4)] и приведя подобные члены, приходим к уравнению
/4)] и приведя подобные члены, приходим к уравнению
2sinx + 2cosx=0, т. е. sinx+cosx=0.
При условии, cosx  0 имеем tgx= -1; х= -
0 имеем tgx= -1; х= -  /4+
/4+  k.
k.
3) Имеем
 (
( 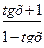 =1)ó(
=1)ó( 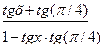 =1)ó(tg(x+
=1)ó(tg(x+ 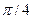 )=1)ó(x+
)=1)ó(x+ 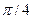 =
= 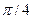 +
+  k) ó
k) ó
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УДВОЕННОГО
АРГУМЕНТА
Формулы для тригонометрических функций удвоенного аргумента позволяют выразить функции аргумента 2  через функции аргумента
через функции аргумента  :
:
sin 2  = 2sin
= 2sin  cos
cos  ; (28)
; (28)
|
|
|
cos 2  = cos2
= cos2  - sin2
- sin2  ; (29)
; (29)
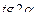 =
= 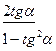 ,
, 
 ,
, 
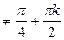 , (30)
, (30)
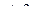 =
= 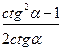 ,
, 
 (31)
(31)
Из формулы легко получаются следующие соотношения
cos 2  =2 cos2
=2 cos2  - 1; (31a)
- 1; (31a)
cos 2  = 1-2 sin2
= 1-2 sin2  . (316)
. (316)
1. Вычислить: 1) sin 2  , если cos
, если cos  =4/5 и 3
=4/5 и 3  /2 <
/2 <  < 2
< 2  ; 2) cos 2
; 2) cos 2  , если cos
, если cos  = -0,2 и
= -0,2 и  /2<
/2<  <
<  ; 3) tg2
; 3) tg2  , если tg
, если tg  =3/4 и
=3/4 и  <
<  <3
<3  /2.
/2.
1) Находим sin  = -
= - 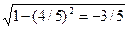 . По формуле (9.42) получим sin 2
. По формуле (9.42) получим sin 2  =2 (-3/5) (4/5) = -24/25.
=2 (-3/5) (4/5) = -24/25.
2) По формуле находим cos2  =2(-0,2)2-1 = -0,92.
=2(-0,2)2-1 = -0,92.
3) По формуле находим 
 =
=  . •
. •
2. Выразить: 1) sin 3  через sin
через sin  ; 2) cos 3
; 2) cos 3  через cos
через cos  .
.
1) sin3  = sin(2
= sin(2  +
+  ) = sin2
) = sin2  cos
cos  +cos2
+cos2  sin
sin  =2sin
=2sin  coscos
coscos  + (1— 2sin2
+ (1— 2sin2  )sin
)sin  = 2sin
= 2sin  cos2
cos2  +sin
+sin  - 2 sin3
- 2 sin3  =2 sin
=2 sin  - sin2
- sin2  )+sin
)+sin  - 2 sin3
- 2 sin3  =2 sin
=2 sin  —2 sin3
—2 sin3  +sin
+sin  - 2sin3
- 2sin3  =3 sin
=3 sin  —4 sin3
—4 sin3  ;
;
2) cos 3  =cos (2
=cos (2  +
+  )=cos 2
)=cos 2  cos
cos  - sin 2
- sin 2  sin
sin  =(2 cos2
=(2 cos2  -1) cos
-1) cos  - 2 sin
- 2 sin  cos
cos  sin
sin  = 2 cos3
= 2 cos3  —cos
—cos  —2 sin2
—2 sin2  cos
cos  =2cos3
=2cos3  —cos
—cos  -
-
2(1 —cos2  )cos
)cos  =2cos3
=2cos3  —cos
—cos  —2cos
—2cos  +2cos3
+2cos3  = 4cos3
= 4cos3  —3cos
—3cos  . •
. •
Дата добавления: 2019-01-14; просмотров: 308; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
