Производные и дифференциалы высших порядков
Определение. Производной второго порядка, или второй производной, функции 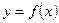 называется производная от ее производной
называется производная от ее производной 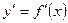 (которую называют первой производной).
(которую называют первой производной).
Обозначения второй производной:  ,
, 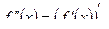
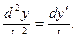
Механический смысл второй производной: если 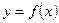 – закон прямолинейного движения точки, то
– закон прямолинейного движения точки, то  – ускорение этого движения в момент времени t.
– ускорение этого движения в момент времени t.
Путем многократного дифференцирования можно получить производную любого порядка. Производная п – го порядка обозначается так:  и так далее.
и так далее.
Пример. Вычислим 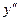 и
и  , если
, если  ;
;  .
.
Решение. В обоих случаях схема выполнения задания одна и та же: последовательное многократное дифференцирование.
1) Найдем производную первого порядка:

Продифференцируем полученное выражение еще раз и, упростив выражение, получим:
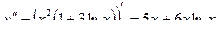
2) Найдем производную первого порядка: 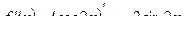
Продифференцируем полученное выражение еще раз:
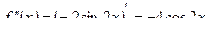
Наконец, продифференцировав выражение в третий раз, получим:
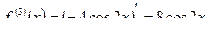
Аналогичным образом вычисляется дифференциал второго и высшего порядков.
Определение. Дифференциал от дифференциала функции 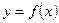 называется вторым дифференциалом или дифференциалом второго порядка и обозначается:
называется вторым дифференциалом или дифференциалом второго порядка и обозначается: 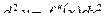
Дифференциал п-го порядка вычисляется следующим образом:

Пример. Вычислим 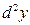 и
и 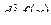 , если
, если  ;
;  .
.
| |
1)  ; 2)
; 2)  .
.
Правило Лопиталя
При вычислении предела отношения  может оказаться, что при
может оказаться, что при  числитель и знаменатель одновременно стремятся к нулю или к бесконечности, т. е. являются одновременно бесконечно малыми или бесконечно большими величинами. Говорят, что в этих случаях мы имеем дело с «неопределенностями» вида
числитель и знаменатель одновременно стремятся к нулю или к бесконечности, т. е. являются одновременно бесконечно малыми или бесконечно большими величинами. Говорят, что в этих случаях мы имеем дело с «неопределенностями» вида  или
или 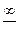 .
.
|
|
|
Вычисление предела в этом случае называется «раскрытием неопределенности» и производится по правилу, указанному французским математиком Гильомом Лопиталем (1661—1704гг.).
Правило Лопиталя . Если функции f (х) и 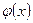 таковы, что:
таковы, что:
1)  и
и 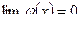 ; или
; или  и
и 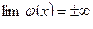 ;
;
2) они имеют первые производные в окрестности точки 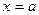 (за возможным исключением самой точки а);
(за возможным исключением самой точки а);
3) существует предел 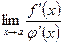 , тогда существует и предел
, тогда существует и предел 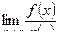 и имеет место равенство
и имеет место равенство 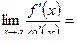
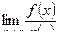 .
.
| |
 или
или 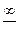 вычисление предела отношения функций, при соблюдении указанных требований, заменяется вычислением предела отношения их производных, которое в большом числе случаев оказывается проще.
вычисление предела отношения функций, при соблюдении указанных требований, заменяется вычислением предела отношения их производных, которое в большом числе случаев оказывается проще.
В случае, когда и отношение производных приводит к одному из этих видов «неопределенностей»  или
или 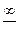 , можно уже к этому отношению применить правило Лопиталя и тем самым исследовать отношение вторых производных. Может оказаться, что и отношение вторых производных дает опять-таки какую-либо из этих «неопределенностей». Тогда следует перейти к отношению третьих производных и т. д. Укажем, что если, понадобится прибегнуть к отношению вторых, третьих и т. д. производных, то прежде чем это делать, следует произвести все возможные упрощения в выражении, полученном на предыдущем этапе.
, можно уже к этому отношению применить правило Лопиталя и тем самым исследовать отношение вторых производных. Может оказаться, что и отношение вторых производных дает опять-таки какую-либо из этих «неопределенностей». Тогда следует перейти к отношению третьих производных и т. д. Укажем, что если, понадобится прибегнуть к отношению вторых, третьих и т. д. производных, то прежде чем это делать, следует произвести все возможные упрощения в выражении, полученном на предыдущем этапе.
|
|
|
Пример.Найдем 1) 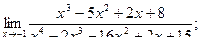 2)
2) 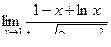 ;
;
3) 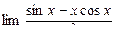 ; 4)
; 4) 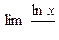 ; 5)
; 5) 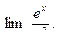
Решение.
1) Если в данную дробь подставить –1 вместо х, то получится неопределенность» вида  . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим:

2) Если в числитель и знаменатель данной дроби подставить 1 вместо х, то получится «неопределенность» вида  . Применяя правило Лопиталя, продифференцируем числитель и знаменатель данной дроби. В итоге получим:
. Применяя правило Лопиталя, продифференцируем числитель и знаменатель данной дроби. В итоге получим:
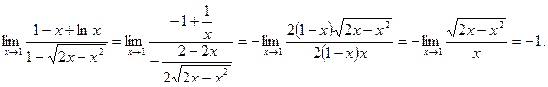
4) Для вычисления данного предела придется операцию дифференцирования произвести несколько раз, так как после первого дифференцирования «неопределенность» не исчезает. Обратите внимание, что после первого дифференцирования произведено упрощение дроби, а после второго применена формула косинуса двойного аргумента:

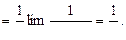
4) В данном случае имеет место «неопределенность» вида 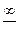 :
:
| |
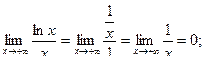
5) Последний пример аналогичен предыдущему:
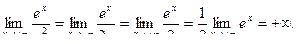
|
|
|
Дата добавления: 2019-01-14; просмотров: 215; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
