Векторы операции над векторами.
Вектор в декартовой системе координат
Определение. Вектором называется упорядоченная пара точек (начало вектора и его конец). Если  ,
,  , то вектор
, то вектор  имеет координаты
имеет координаты 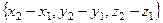 .
.
Вектор  в координатном пространстве Oxyz, может быть представлен в виде
в координатном пространстве Oxyz, может быть представлен в виде
 , где тройка
, где тройка 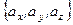 называется координатами вектора. Векторы
называется координатами вектора. Векторы  – единичные векторы (орты), направленные в положительную сторону координатных осей Ox, Oy и Oz, соответственно. Длиной (модулем) вектора
– единичные векторы (орты), направленные в положительную сторону координатных осей Ox, Oy и Oz, соответственно. Длиной (модулем) вектора 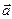 называется число
называется число  .
.
Линейные операции с векторами
 |
Сложение векторов определяется по правилу параллелограмма: вектор  является диагональю параллелограмма, построенного на векторах
является диагональю параллелограмма, построенного на векторах 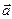 и
и  (рис.1а).
(рис.1а).
Разность двух векторов 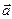 и
и  определяется по формуле
определяется по формуле  , где
, где  – вектор той же длины, что и вектор
– вектор той же длины, что и вектор  , но противоположно направленный. Чтобы найти вектор-разность
, но противоположно направленный. Чтобы найти вектор-разность 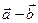 нужно отложить векторы
нужно отложить векторы 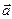 и
и  из общей точки, соединить концы векторов вектором, направленным от «вычитаемого» к «уменьшаемому» (то есть от
из общей точки, соединить концы векторов вектором, направленным от «вычитаемого» к «уменьшаемому» (то есть от  к
к 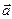 ) (рис.1б). Построенный вектор и будет искомой разностью.
) (рис.1б). Построенный вектор и будет искомой разностью.
При сложении нескольких векторов каждая координата суммы есть сумма соответствующих координат слагаемых векторов, при умножении вектора на данное число 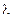 на это же число умножаются и координаты вектора:
на это же число умножаются и координаты вектора:
а)  ;
;
б)  , где
, где 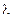 – скалярный множитель.
– скалярный множитель.
Несколько векторов называются коллинеарными (компланарными), если они параллельны одной и той же прямой (плоскости). Векторы  и
и  параллельны (коллинеарны), то есть соответствующие координаты этих векторов пропорциональны с одним и тем же коэффициентом пропорциональности:
параллельны (коллинеарны), то есть соответствующие координаты этих векторов пропорциональны с одним и тем же коэффициентом пропорциональности:  .
.
|
|
|
Базис на плоскости и в пространстве
Определение. Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы  образуют базис в декартовом координатном пространстве Oxyz.
образуют базис в декартовом координатном пространстве Oxyz.
Пример 1.
Даны векторы  . Показать, что векторы
. Показать, что векторы 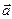 и
и  образуют базис на плоскости и найти координаты вектора
образуют базис на плоскости и найти координаты вектора  в этом базисе.
в этом базисе.
Решение. Если два вектора неколлинеарны (  ), то они образуют базис на плоскости. Так как
), то они образуют базис на плоскости. Так как  , то векторы
, то векторы 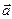 и
и  неколлинеарны и, значит, образуют базис. Пусть в этом базисе вектор
неколлинеарны и, значит, образуют базис. Пусть в этом базисе вектор  имеет координаты
имеет координаты  , тогда разложение вектора
, тогда разложение вектора  по векторам
по векторам 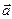 и
и  имеет вид
имеет вид  , или в координатной форме
, или в координатной форме
 или
или 
Решив полученную систему уравнений каким-либо образом, получим, что  .
.
Значит 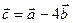 . Таким образом, в базисе
. Таким образом, в базисе 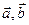 вектор
вектор  имеет координаты
имеет координаты  .
.
Скалярное, векторное, смешанное произведение векторов.
Определение. Скалярным произведением двух векторов  и
и 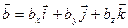 называется число, определяемое равенством:
называется число, определяемое равенством:
|
|
|
 ,
,
где  – угол между векторами
– угол между векторами 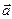 и
и  . Если
. Если  , то
, то  .
.
Зная скалярное произведение, можно определить угол между двумя векторами по формуле:  .
.
Условие перпендикулярности ненулевых векторов (угол между ними равен 90°) имеет вид:  , или
, или 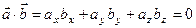 , а условие их коллинеарности:
, а условие их коллинеарности: 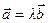 , или
, или  .
.
Свойства скалярного произведения:
1) 
 ; 2)
; 2)  ; 3)
; 3) 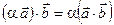 ; 4)
; 4)  , причем
, причем  .
.
Пример 2. Найти угол между векторами  и
и  , если
, если 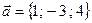 ,
,  ,
, 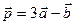 ,
,  .
.
Решение. Используем формулу  . Определим координаты векторов
. Определим координаты векторов  и
и  , учитывая, что при сложении векторов мы складываем одноименные координаты, а при умножении вектора на число – умножаем на это число каждую координату этого вектора, а:
, учитывая, что при сложении векторов мы складываем одноименные координаты, а при умножении вектора на число – умножаем на это число каждую координату этого вектора, а: 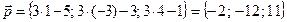 ,
,  .
.
Найдем скалярное произведение векторов  и
и  и их длины.
и их длины.  ,
,  ,
,  . Подставив в формулу, получим
. Подставив в формулу, получим 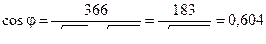 . Отсюда
. Отсюда  .
.
Определение. Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  (другое обозначение
(другое обозначение  ), который:
), который:
а) имеет длину  , где
, где  – угол между векторами
– угол между векторами  и
и  ;
;
б) перпендикулярен векторам  и
и  (
( 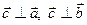 ) (то есть, перпендикулярен плоскости, в которой лежат векторы
) (то есть, перпендикулярен плоскости, в которой лежат векторы  и
и  );
);
в) направлен так, что векторы  ,
,  ,
,  образуют правую тройку векторов, то есть из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки (рис.2).
образуют правую тройку векторов, то есть из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки (рис.2).
|
|
|
Координаты векторного произведения вектора  на вектор
на вектор  определяются по формуле:
определяются по формуле:
 |

Геометрический смысл векторного произведения: модуль вектора  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  .
.
Свойства векторного произведения:
1) 
 ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 
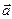 и
и  коллинеарны.
коллинеарны.
 |
Пример 3. Параллелограмм построен на векторах
 и
и  , где
, где  ,
, 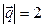 ,
, 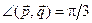 . Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
Решение.
 ,
,  ,
,

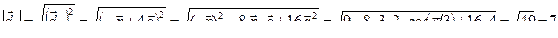 .
.
Угол между диагоналями обозначим буквой  , тогда
, тогда

Следовательно, 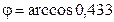 .
.
Используя свойства векторного произведения, вычислим площадь параллелограмма:

Определение. Смешанным произведением трех векторов  ,
,  ,
,  называется скалярное произведение вектора
называется скалярное произведение вектора 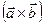 на вектор
на вектор  :
:
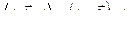 .
.
Если  то смешанное произведение можно вычислить по формуле:
то смешанное произведение можно вычислить по формуле:
 .
.
Свойства смешанного произведения:
1) При перестановке любых двух векторов смешанное произведение меняет знак;
2)  ; 3)
; 3)  ;
;
4)  компланарны
компланарны  .
.

Геометрический смысл смешанного произведения: объем  параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах  ,
,  ,
,  (рис.4), а объем
(рис.4), а объем 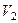 образованной ими треугольной пирамиды находятся по формулам
образованной ими треугольной пирамиды находятся по формулам  .
.
|
|
|
Пример 4. Компланарны ли векторы  ,
, 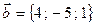 ,
, 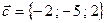 ?
?
Решение. Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:
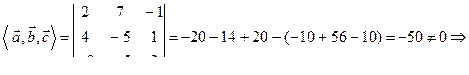 векторы
векторы  ,
,  ,
,  некомпланарны.
некомпланарны.
Деление отрезка в данном отношении.
Пусть отрезок  в пространстве Oxyz задан точками
в пространстве Oxyz задан точками 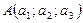 и
и  . Если он разделен точкой
. Если он разделен точкой  в отношении
в отношении  , то координаты точки
, то координаты точки  следующие:
следующие:
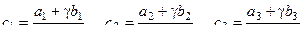 .
.
Пример 5. Найти точку  , делящую отрезок
, делящую отрезок  в отношении
в отношении  , если
, если  .
.
Решение. Определим координаты точки  :
:
 . Таким образом,
. Таким образом,  .
.
Контрольные вопросы
Контрольные задания
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить все задания любого из трёх предложенных вариантов, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 8
«Прямые и плоскости в пространстве»
Цель:
¾ формирование навыков построения чертежей пространственных фигур на плоскости;
¾ формирование навыков записи краткого условия задачи математическими символами;
¾ формирование навыков решения задач на прямые и плоскости в пространстве
|
|
Стереометрия.
Введение
Предмет стереометрии.
Курс геометрии состоит из двух частей: планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур на плоскости. Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» — объемный, пространственный и «метрео» — измерять.
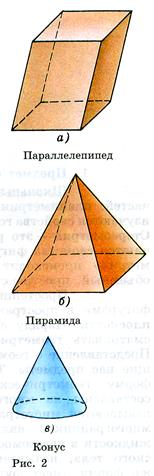
Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости. Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности. Представление о геометрических телах дают окружающие нас предметы. Так, например, кристаллы имеют форму геометрических тел, поверхности которых составлены из многоугольников. Такие поверхности называются многогранниками. Одним из простейших многогранников является куб (рис. 1, а). Капли жидкости в невесомости принимают форму геометрического тела, называемого шаром (рис. 1, б). Такую же форму имеет футбольный мяч. Консервная банка имеет форму геометрического тела, называемого цилиндром (рис. 1, в).
В отличие от реальных предметов геометрические тела, как и всякие геометрические фигуры, являются воображаемыми объектами. Мы представляем геометрическое тело как часть пространства, отделенную от остальной части пространства поверхностью — границей этого тела. Так, например, граница шара есть сфера, а граница цилиндра состоит из двух кругов — оснований цилиндра и боковой поверхности.
Изучая свойства геометрических фигур — воображаемых объектов, мы получаем представление о геометрических свойствах реальных предметов (их форме, взаимном расположении и т. д.) и можем использовать эти свойства в практической деятельности.
|
|
В этом состоит практическое (прикладное) значение геометрии. Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
При изучении пространственных фигур, в частности геометрических тел, пользуются их изображениями на чертеже. Как правило, изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения. Обычно выбирается то из них, которое создает правильное представление о форме фигуры и наиболее удобно для исследования ее свойств. На рисунках 2, а, б изображены два многогранника — параллелепипед и пирамида,. а на рисунке 2, в — конус. При этом невидимые части этих фигур изображены штриховыми линиями. Правила изображения пространственных фигур приведены в приложении 1.
В X классе мы будем изучать взаимное расположение прямых и плоскостей, многогранники и векторы в пространстве, а в XI классе — метод координат в пространстве, «круглые» геометрические тела — цилиндр, конус, шар и рассмотрим вопрос об объемах тел.
Аксиомы стереометрии.
 В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается еще одна основная фигура — плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается еще одна основная фигура — плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
Как и ранее, точки будем обозначать прописными латинскими буквами А, В, С и т. д., а прямые — строчными латинскими буквами а, b , с и т. д. или двумя прописными латинскими буквами АВ, CD и т. д. Плоскости будем обозначать греческими буквами α, β, γ и т. д. На рисунках плоскости изображаются в виде параллелограмма (рис. 3, а) или в виде произвольной области (рис. 3, б).
Ясно, что в каждой плоскости лежат какие-то точки пространства, но не все точки пространства лежат в одной и той же плоскости. На рисунке 3, б точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки М, Н, Р не лежат в этой
плоскости. Коротко это записывают так: А Є β, В Є β, М ¢ β, N ¢ β, P ¢ β.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, большая часть которых нам знакома по курсу планиметрии. Полный список аксиом и некоторые следствия из них приведены в приложении 2. Здесь мы сформулируем лишь три аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве. Ниже они обозначены А1, А2, А3.
 А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Иллюстрацией к этой аксиоме может служить модель, изображенная на рисунке 4. Плоскость, проходящую через точки А, В и С, не лежащие на одной прямой, иногда называют плоскостью АВС.
Отметим, что если взять не три, а четыре произвольные точки, то через них может не проходить ни одна плоскость. Иначе говоря, четыре точки могут не лежать в одной плоскости. Каждый знаком с таким наглядным подтверждением этого факта: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, т. е. опирается на три «точки», а конец четвертой ножки (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.
А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

В таком случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую (рис. 5, а).
Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.
Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются (рис 5, б).
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
 В таком случае говорят, что плоскости пересекаются по прямой (рис. 5, в). Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
В таком случае говорят, что плоскости пересекаются по прямой (рис. 5, в). Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
Прежде чем перейти к первым следствиям из данных аксиом, отметим одно важное обстоятельство, которым будем пользоваться в дальнейшем. В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии. Более того, признаки равенства и подобия треугольников, известные из курса планиметрии, справедливы и для треугольников, расположенных в разных плоскостях.
Дата добавления: 2019-01-14; просмотров: 254; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!