Признак перпендикулярности двух плоскостей
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 61, а). Если один из этих двугранных углов равен φ, то другие три угла равны соответственно 180°-φ, φ и 180°-φ. В частности, если один из углов прямой (φ = 90°), то и остальные три угла прямые. Если φ — тот из четырех углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ. Очевидно, 0°<φ≤90°.
Определение
 Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90° .
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90° .
Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты.
Ясно, что все четыре двугранных угла, образованные взаимно перпендикулярными плоскостями, прямые.
Теорема (признак перпендикулярности плоскостей).
 Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 63)
Контрольные вопросы
1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
2. Точка М не лежит на прямой а. Сколько прямых, не пересекающих прямую а, проходит через точку М? Сколько из этих прямых параллельны прямой а?
3. Прямые а и с параллельны, а прямые а и b пересекаются. Могут ли прямые b и с быть параллельными?
4. Прямая а параллельна плоскости а. Верно ли, что эта прямая:
А) не пересекает ни одну прямую, лежащую в плоскости а;
Б) параллельна любой прямой, лежащей в плоскости а;
В) параллельна некоторой прямой, лежащей в плоскости а?
5. Прямая а параллельна плоскости а. Сколько прямых, лежащих в плоскости а, параллельны прямой а? Параллельны ли друг другу эти прямые, лежащие в плоскости а?
6. Прямая а пересекает плоскость а. Лежит ли в плоскости а хоть одна прямая, параллельная а?
7. Одна из двух параллельных прямых параллельна некоторой плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости?
8. Верно ли утверждение: если две прямые параллельны некоторой плоскости, то они параллельны друг другу?
9. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:
а) пересекаться; б) быть скрещивающимися?
10. могут ли скрещивающиеся прямые а и b быть параллельными прямой с?
11. Боковые стороны трапеции параллельны плоскости а. Параллельны ли плоскость а и плоскость трапеции?
12. Две стороны параллелограмма параллельны плоскости а. Параллельны ли плоскость а и плоскость параллелограмма?
13. Могут ли быть равны два непараллельных отрезка, заключённые между параллельными плоскостями?
14. Существует ли тетраэдр, у которого пять углов граней прямые?
15. Существует ли параллелепипед, у которого: а) только одна грань – прямоугольник; б) только две смежные грани – ромбы; в) все углы граней острые; г) все углы граней прямые; д) число всех острых граней не равно числу всех тупых углов граней?
16. Какие многоугольники могут получиться в сечении:
а)тетраэдра; б)параллелепипеда?
17.Верно ли утверждение: если две прямые в пространстве перпендикулярны к третьей прямой, то эти прямые параллельны? Верно ли это утверждение при условии, что все три прямые лежат в одной плоскости?
18.Параллельные прямые b и с лежат в плоскости а, а прямая а перпендикулярна к прямой b. Верно ли утверждение: а) прямая а перпендикулярна к прямой с; б) прямая а пересекает плоскость а?
19.Прямая а перпендикулярна к плоскости а, а прямая b не перпендикулярна к этой плоскости. Могут ли прямые а и b быть параллельными?
20.Прямая а параллельна к плоскости а, а прямая b перпендикулярна к этой плоскости. Верно ли утверждение, что прямые а и b взаимно перпендикулярны?
21.Прямая а параллельна плоскости а, а прямая b перпендикулярна к этой плоскости. Существует ли прямая, перпендикулярная к прямым а и b?
22.Вероно ли утверждение, что все прямые, перпендикулярные к данной плоскости и пересекающие данную прямую, лежат в одной плоскости?
23.Могут ли две плоскости, каждая из которых перпендикулярна к третьей плоскости, быть: а) параллельными плоскостями; б) перпендикулярными плоскостями?
24.Можно ли через точку пространства провести три плоскости, каждые две из которых взаимно перпендикулярны?
25.Диагональ квадрата перпендикулярна к некоторой плоскости. Как расположена другая диагональ квадрата по отношению к этой плоскости?
26.Сколько двухгранных углов имеет: а) тетраэдр; б) параллелепипед?
Контрольные задания
1. Катеты прямоугольного треугольника 14дм и 48дм. Перпендикуляр к плоскости треугольника, восстановленный из вершины прямого угла, равен 60дм.
Найти расстояние от концов перпендикуляра до центра окружности, описанной около данного треугольника.
2. Из точки взятой вне плоскости, проведены к плоскости α перпендикуляр и наклонные. Одна из наклонных равна 12см и образует с перпендикуляром угол в 60º.
Найти проекции этих наклонных, если вторая наклонная имеет длину 10см.
3. К плоскости правильного треугольника АВС в его центре О восстановлен перпендикуляр ОМ, равный 8см.
Найти расстояние точки М от вершин и сторон треугольника, если площадь его равна 27√3см².
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить все задания из предложенного варианта, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 9
«Геометрические тела и их поверхности. Объёмы геометрических тел
(Многогранники)»
Цели:
¾ формирование навыков построения чертежей пространственных фигур на плоскости;
¾ формирование навыков записи краткого условия задачи математическими символами;
¾ формирование навыков решения задач
Многогранники
Призма

Призмой называется многогранник, две грани которого произвольные многоугольники, лежащие в параллельных плоскостях, а остальные грани - параллелограммы.
Призма называется прямой, если её боковые рёбра перпендикулярны плоскости основания.
Прямая призма называется правильной, если в основании правильный многоугольник.
Параллелепипедом называется призма, все грани которой – параллелограммы.
Параллелепипед называется прямым, если его боковые рёбра перпендикулярны плоскости основания.
Прямой параллелепипед называется прямоугольным, если в основании прямоугольник.
Sб = PoH - площадь боковой поверхности призмы
Sп = PoH + 2 So - площадь полной поверхности призмы
V= So H – объём призмы
Пирамида
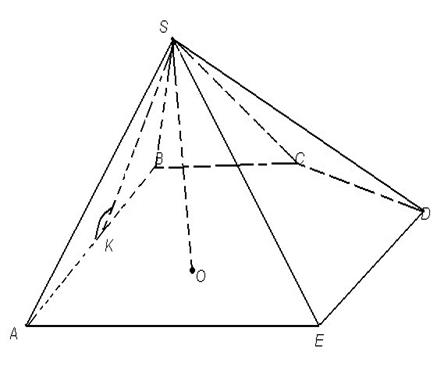
Пирамидой называется многогранник, одна грань которого произвольный многоугольник, а остальные грани треугольники, имеющие общую вершину.
Пирамида называется правильной, если в основании правильный многоугольник, и высота падает в центр основания.
Высота боковой грани правильной пирамиды называется апофемой.
Sб = 1/2 PoHб - площадь боковой поверхности правильной пирамиды
Sп = Sб + So - площадь полной поверхности пирамиды
V= 1/3 So H – объём пирамиды
Усечённая пирамида
Усечённой пирамидой называется часть пирамиды, заключённая между основанием и плоскостью, параллельной основанию.
Усечённая пирамида называется правильной, если в основаниях
правильные многоугольники, а высота соединяет центры оснований.
Высота боковой грани правильной усечённой пирамиды называется
апофемой.
Sб = 1/2( Pн. o +Рв.о) Hб - площадь боковой поверхности правильной
Усечённой пирамиды
Sп = Sб + Sн. o + Sв. o - площадь полной поверхности усечённой пирамиды
V= 1/3 H( Sн. o + 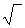 Sн. o Sв. o + Sв. o)
Sн. o Sв. o + Sв. o)  – объём усечённой пирамиды.
– объём усечённой пирамиды.
Примеры решения задач
1.Прямоугольный треугольник с катетами 12см и 16см. Найдите расстояние от точки, до плоскости треугольника, если расстояния от этой точки до каждой вершины треугольника равны 26 см.

Дано:
 АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение: АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение:
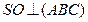 Т.к. |SA|=|SB|=|SC|, то
Т.к. |SA|=|SB|=|SC|, то 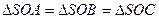 (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около 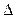 ABC, а т.к. ABC, а т.к. 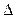 ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO| ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO|
|
Решение:
Рассмотрим 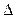 АВС. По теореме Пифагора |AB|=
АВС. По теореме Пифагора |AB|= 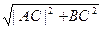
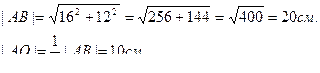
Рассмотрим 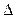 SOA-прямоугольный, т.к. SO
SOA-прямоугольный, т.к. SO 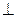 (ABC), по теореме Пифагора
(ABC), по теореме Пифагора
|SO|= 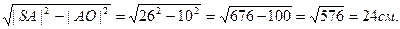
Ответ: |SO|=24 см.
2.В прямом параллелепипеде стороны основания равны 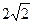 см и 5см и образуют угол в
см и 5см и образуют угол в 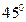 , меньшая диагональ параллелепипеда равна 7 см.
, меньшая диагональ параллелепипеда равна 7 см.
Найдите длину бокового ребра параллелепипеда.
B1
C1
 A1
D1
B C
A D
A1
D1
B C
A D
|
Дано:
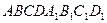 - прямой параллелепипед .
|AB|= - прямой параллелепипед .
|AB|= 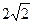 см., |AD|=5 см., см., |AD|=5 см., 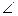 BAD= BAD= 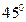 ; | ; | 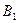 D|=7 см.
Найти. |B D|=7 см.
Найти. |B 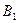 | |
|
Решение:
Рассмотрим треугольник ABD.
По теореме косинусов:
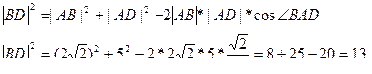
Рассмотрим треугольник 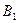 BD- прямоугольный;
BD- прямоугольный;
Т.к. параллелепипед прямой то по теореме Пифагора:
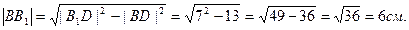
Ответ: | 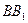 | = 6 см.
| = 6 см.
3.Основанием пирамиды является треугольник со сторонами 39 см, 17 см, 28см, боковые рёбра равны каждое 22,9 см.
Найдите высоту пирамиды.
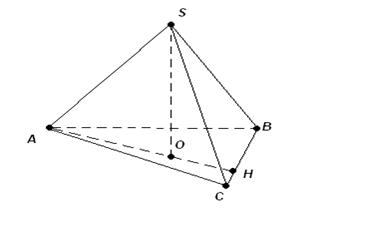
| Дано:
SABC-пирамида, |AB|=39 см, |BC|=17 cм, |AC|=28 см,
|SA|=|SB|=|SC|=22,9 см.
Построение:
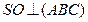 Т.к. |SA|=|SB|=|SC| то, О-центр описанной около
Т.к. |SA|=|SB|=|SC| то, О-центр описанной около  АВС окружности.
Найти |SO|. АВС окружности.
Найти |SO|.
|
Решение:
Рассмотрим  АВС. Найдём площадь этого треугольника по формуле Герона:
АВС. Найдём площадь этого треугольника по формуле Герона:
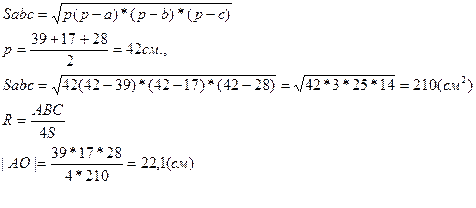
Рассмотрим  SOA-прямоугольный, т.к.
SOA-прямоугольный, т.к. 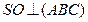 .
.
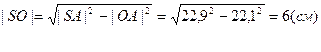
Ответ. |SO| = 6 см.
4.В прямом параллелепипеде стороны основания равны 1 м и 2 м и образуют угол в 600. Большая диагональ параллелепипеда равна 4 м. Найдите объем и боковую поверхность параллелепипеда.
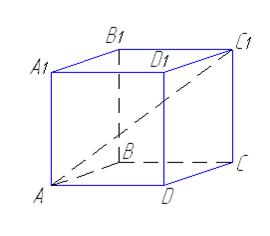
Решение:
V = Soh; Sбок = Роснh
So= 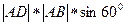 = 2 = 2 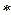 1 1 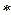 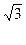 = = 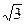 (м2)
По теореме косинусов: (м2)
По теореме косинусов: 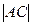 2 = 2 = 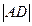 2 + 2 + 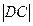 2 – 2 2 – 2 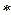 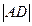  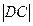  cos1200 = 22 + 12 – 2 cos1200 = 22 + 12 – 2 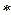 2 2 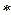 1 1 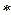 (- (- 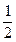 ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: 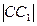 = = 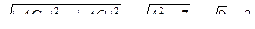 (м).
V = (м).
V = 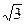 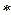 3 = 3 3 = 3 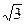 (м3).
Sбок = (2+1) (м3).
Sбок = (2+1)  2 2 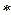 3 = 18 (м2).
Ответ. V = 3 3 = 18 (м2).
Ответ. V = 3 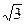 (м3), Sбок = 18 (м2). (м3), Sбок = 18 (м2).
| Дано:
ABCDA1B1C1D1 – прямой параллелепипед
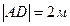 , , 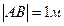 , , 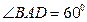 , , 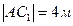 .
Найти: V, Sбок .
Найти: V, Sбок
|
Контрольные вопросы
- Дайте определение многогранника.
- Сформулируйте определение призмы.
- Сформулируйте определение параллелепипеда.
- Сформулируйте определение пирамиды.
- Сформулируйте определение правильной пирамиды.
- Сформулируйте определения элементов пирамиды.
- Сформулируйте определение усечённой пирамиды.
Контрольные задачи
1. Катеты прямоугольного треугольника АВС равны 15 м и 20 м. Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр CD=35 м. Найдите расстояние от точки D до гипотенузы АВ.
2. Стороны треугольника 10 см, 17 см и 21 см. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15 см. Определить расстояние от его концов до большей стороны
3. Из точки, отстоящей от плоскости на расстоянии 2 см, проведены две наклонные, образующие с плоскостью углы в 450, а между собой угол в 600. Найти расстояние между концами наклонных
4. Стороны треугольника равны 17, 15 и 8 см. Через вершину А меньшего угла треугольника проведена прямая АМ, перпендикулярная к его плоскости. Найти расстояние от точки М до прямой, содержащей меньшую сторону треугольника, если длина отрезка АМ равна 20 см.
5. Из точки, отстоящей от плоскости на расстоянии 3 см, проведены две наклонные, образующие с плоскостью углы в 450 и 300, а между собой прямой угол. Найти расстояние между концами наклонных.
6. Из точки K, удаленной от плоскости  на 9 см, проведены к плоскости
на 9 см, проведены к плоскости  две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
7. Из вершины прямого угла прямоугольного треугольника с катетами 15 см и 20 см проведен перпендикуляр длиной 16 см к плоскости треугольника. Найти расстояние от концов перпендикуляра до гипотенузы.
8. Стороны треугольника равны 15, 37 и 44 см. Из вершины большего угла треугольника восстановлен к его плоскости перпендикуляр, равный 16 см. Найти расстояние от его концов до большей стороны.
9. Стороны треугольника равны 51, 30 и 27 см. Из вершины меньшего угла треугольника проведен к его плоскости перпендикуляр, равный 10 см. Найти расстояние от его концов до противоположной стороны треугольника.
10. В треугольнике АВС длина отрезка АВ равна 13 см, длина отрезка ВС равна 14 см, длина отрезка АС равна 15 см. Из вершины А восстановлен к плоскости треугольника перпендикуляр AD, равный 5 см. Найти расстояние от точки D до стороны ВС.
11. В прямом параллелепипеде стороны основания равны 3см и 5см и образуют угол в 60◦. Площадь большого диагонального сечения равна 63 см2. Найдите боковое ребро параллелепипеда.
12. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 60◦. Найдите высоту пирамиды.
13. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 45◦. Найдите площадь боковой поверхности и объем пирамиды.
14. Стороны основания прямой треугольной призмы равны 3 см, 25 см и 26 см, а площадь большей боковой грани равна 260 см2. Найдите боковое ребро призмы.
15. Основание пирамиды – треугольник со сторонами, равными 6 см, 10 см и 14 см. каждый двугранный угол при основании равен 300. Найдите высоту пирамиды.
16. В прямом параллелепипеде стороны основания равны 3 дм и 8 дм, угол между ними 600. Зная, что большая диагональ параллелепипеда равна 49 дм, найдите боковую поверхность и объем параллелепипеда.
17. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 600. Найдите полную поверхность пирамиды и объем.
18. Стороны прямого параллелепипеда равны 5см и 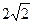 см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
19. Основанием пирамиды служит равнобедренный треугольник, основание которого 12см и высота 18см. каждое из боковых ребер равно 26см. найдите высоту пирамиды.
20. Основанием пирамиды служит треугольник со сторонами, равными 6 см, 10 см, 14 см. Каждый двугранный угол при основании равен 300. Найдите площадь боковой поверхности и объем этой пирамиды.
21. Основанием пирамиды служит треугольник со сторонами, равными 6 см, 10 см, 14 см. Каждый двугранный угол при основании равен 300. Найдите площадь боковой поверхности и объем этой пирамиды.
22. В основании пирамиды лежит равнобедренный треугольник, основание которого равно 12 дм, а боковая сторона 10 дм. Все боковые грани образуют с основанием углы 450. Найдите площадь боковой поверхности и объем пирамиды.
23. Основанием пирамиды DABC служит треугольник со сторонами AB=AC=13см, BC=10см, ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите высоту грани DBC.
24. Основание пирамиды – равнобедренный треугольник, у которого основание равно 6 см, а высота 9 см, боковые ребра равны между собой и каждое содержит 13 см. Найдите объем пирамиды.
25. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 12см, а боковая сторона 10 см. Боковые грани образуют с основанием равные углы по 45◦ . Найдите высоту пирамиды.
26. Стороны прямого параллелепипеда равны 5 см и 2 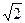 см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
27. Стороны прямого параллелепипеда равны 5 см и 2 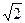 см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
28. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см, каждое боковое ребро пирамиды равно 13 см. Найдите объем пирамиды.
29. Боковое ребро и апофема правильной треугольной пирамиды соответственно равны 10 см и 6 см. Найдите стороны основания этой пирамиды.
30. В правильной четырехугольной усеченной пирамиде стороны оснований 16 м и 4 м. Найдите площадь полной поверхности и объем, если высота пирамиды равна 8 м.
31. Основанием пирамиды является треугольник со сторонами 10 см, 10 см и 12 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите высоту пирамиды.
32. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите площадь полной поверхности и объем параллелепипеда.
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить не менее 25 задач из предложенных, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 10
«Геометрические тела и их поверхности. Объёмы геометрических тел
(Круглые тела)»
Цели:
¾ формирование навыков построения чертежей пространственных фигур на плоскости;
¾ формирование навыков записи краткого условия задачи математическими символами;
¾ формирование навыков решения задач
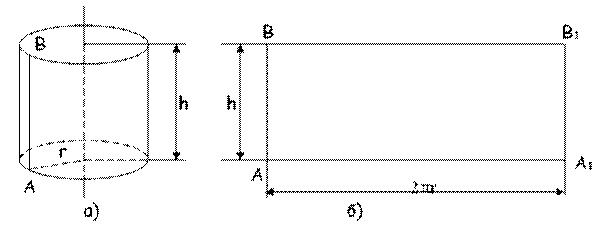
Цилиндр
Дата добавления: 2019-01-14; просмотров: 483; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
