Цилиндр- тело, полученное при вращении прямоугольника вокруг одной из своих сторон.

S_б = 2Пrh - площадь боковой поверхности цилиндра

S_п = 2Пrh + 2Пr² - площадь полной поверхности цилиндра

V=Пr²h – объём цилиндра

 

Конус

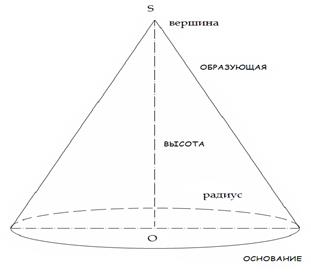
Конус – тело, полученное вращением прямоугольного треугольника вокруг его катета, являющегося высотой конуса.

S_б = Пrl - площадь боковой поверхности конуса

S_п = Пrl + Пr² - площадь полной поверхности конуса

V=1/3Пr²h – объём конуса

 

Усечённый конус

 

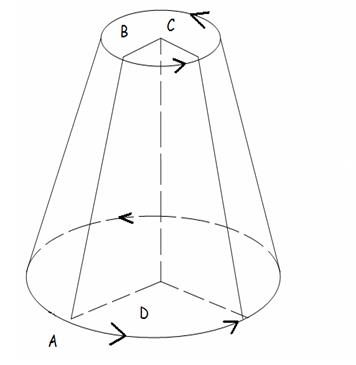
Усечённым конусом называется часть конуса, заключённая между основанием конуса и плоскостью, параллельной основанию

S_б = П(R+r)l - площадь боковой поверхности усечённого конуса

S_п = Пl(R+r) + Пr²+ПR² - площадь полной поверхности усечённого конуса

V=1/3Пh(r² + R² +Rr) – объём усечённого конуса

 

 

Сфера и шар

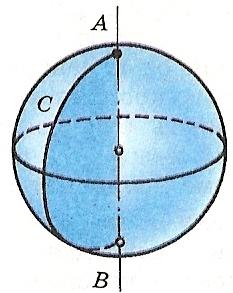
Площадь поверхности и объём шара

Sш.= 4П R²

Vш.=4/3П R³

 

Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

 

Радиус сферы R – отрезок соединяющий центр и любую точку сферы.

 

Диаметр сферы – отрезок соединяющий 2 точки сферы и проходящий через её центр, равный 2R.

 

Шар – тело полученное при вращении полукруга вокруг его диаметра.

 

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ.

 

Возможны 3 случая:

1. d<R, тогда R²-d²>0, все точки этой окружности являются общими точками окружности и сферы.

Если расстояние от центра сферы до плоскости <R сферы, то сечение сферы плоскостью – окружность.

Если секущая плоскость проходит через центр шара, то d=0 – больший круг шара.

2.  d=R, тогда R²-d²=0

О – общая точка сферы и плоскости

Если расстояние от центра сферы до плоскости равно R сферы, то они имеют только одну общую точку.

3.  d>R, тогда R²-d²<0.

Если расстояние от центра сферы до плоскости больше R сферы, то они не имеют общих точек.

 

Касательная плоскость.

Касательной плоскостью к шаровой поверхности называется плоскость, имеющая с этой поверхностью только одну общую точку.

Теорема. Плоскость, перпендикулярная к радиусу сферы в его конце, лежащем на сфере, есть касательная плоскость.

Дано: а к радиусу ОА в его конце А

Требуется доказать, что любая точка плоскости а, кроме точки А, лежит вне сферы.

Доказательство. Возьмём на плоскости произвольную точку М, отличную от точк и А, и соединим прямой точки М и О. Получим:

МО – наклонную и АО – перпендикуляр к плоскости а. Получаем что МО >АО т. е. точка М лежит вне сферы. Следовательно, у сферы и плоскости а только одна общая точка А, т. е. плоскость а – касательная к сфере.

Части шара

1. Шаровой сегмент -  тело, отсекаемое от шара плоскостью.

Отрезок радиуса, перпендикулярного к плоскости сечения, между этой плоскостью и поверхностью шара называется высотой сегмента.

Sшар.сегм.=2П Rh; Vшар.сегм.= П h ( R- h/3)

 

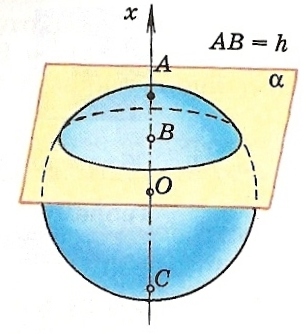
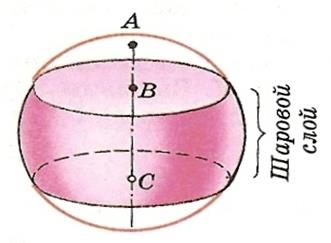
2. Шаровой слой - тело, отсекаемое от шара двумя параллельными плоскостями. Сферическая поверхность шарового слоя называется шаровым поясом.

Расстояние между параллельными плоскостями называется высотой шарового слоя.

 

 

 

 

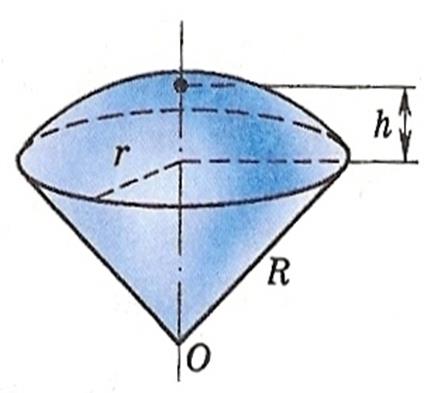
3. Простой шаровой сектор - тело, полученное вращением кругового сектора вокруг своего радиуса.

Если ось вращения не совпадает с радиусом, ограничивающим круговой сектор, то в результате вращения этого сектора вокруг оси получается полый шаровой сектор.

Vшар.сек.= 2/3П R h

 

 

Примеры решения задач

1. Образующая конуса равна 6 см и наклонена к плоскости основания под углом 60⁰. Найдите высоту конуса.

 

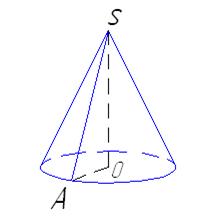
Дано: Конус, |SA|=6 см, SAO= 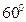. Найти |SO|.

Решение:

Рассмотрим 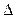SOА - прямоугольный.

sin 60 ⁰ =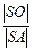

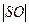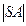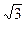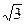 =  sin 60 ⁰ = 6  = 3  см.

Ответ. |SO| = 3 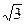 см.

2.Площадь основания конуса равна 16 дм², а боковая поверхность 20 дм² . Найдите объем конуса.

Дано: конус; So = 16 дм2, Sбок = 20 дм2. Найти: V

Решение:

V = 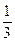 S_oh;

Так как в основании конуса лежит круг, то 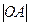² = 16 ;

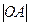                                                                       ² = 16;

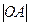                                                                        = 7 (дм).

S_бок = .

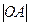
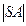Подставим в формулу 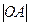 = 4, S_бок = 20 .

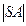4  = 20 ;

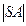 = 5 (дм).

Рассмотрим прямоугольный треугольник SOA. По теореме Пифагора |SO|=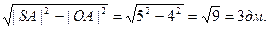  

V = 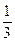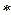16 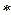3 = 16  (дм³).

Ответ. V = 16  (дм³).

 

Контрольные задачи

 

1. Площадь осевого сечения цилиндра равна 10 м², а площадь основания - 4  м². Найдите высоту цилиндра.

 

2. Высота и образующая конуса относятся как 35:37. Полная поверхность конуса равна 588  см². Найдите площадь боковой поверхности и объем конуса.

 

3. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.

 

4. Радиусы оснований усеченного конуса и его высота относятся как 3:6:4. Вычислите боковую поверхность и объем конуса, если его образующая равна 25 см.

 

5. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше радиуса другого, а образующая наклонена к основанию под углом 450. Найдите боковую поверхность и объем этого конуса.

6. Шар радиуса 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения.

7. Боковая поверхность конуса 15 дм2, а полная поверхность 24 дм². Найдите объем конуса.

8. Боковая поверхность конуса 15 дм², а полная поверхность 24 дм². Найдите объем конуса.

9. Образующая усеченного конуса равна 4 см и наклонена к плоскости основания под углом 60⁰. Зная, что радиус большего основания равен 5 см, найдите боковую поверхность и объем усеченного конуса.

10. Угол между образующей и осью конуса равен 45⁰, образующая равна 6,5 см. Найдите радиус основания конуса.

11. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше другого, а образующая наклонена к основанию под углом 450. Найдите площадь боковой поверхности и объем этого конуса.

12. Радиусы оснований усеченного конуса равны 5 см и 11 см, образующая равна 10 см. Найдите высоту усеченного конуса.

13. Площадь основания конуса 9 см² , полная поверхность его 24 см² . Найдите объем конуса.

14. Площадь основания конуса 9 см² , полная поверхность его 24 см². Найдите объем конуса.

15. Высота цилиндра на 10 см больше радиуса его основания, площадь полной поверхности равна 264 см². Найдите площадь боковой поверхности и объем цилиндра.

16. Образующая конуса наклонена к плоскости основания под углом 300. Найдите образующую, если радиус основания конуса равен 6 см.

17. Радиусы оснований усеченного конуса 6 м и 2 м, образующая наклонена к основанию под углом 45⁰. Найдите площадь боковой поверхности и объем конуса.

 

18. Шар пересекает плоскость на расстоянии 9 см от центра, площадь сечения

       1600 см². Найдите радиус шара

 

19. Поверхность шара равна 225 м². Определите его объем.

Сроки выполнения задания: при изучении данной темы, в течение семестра.

 

Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить не менее 15 задач из предложенных, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.

 

---

Дата добавления: 2019-01-14; просмотров: 618; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!