Геометрические приложения определенного интеграла

Пусть функция 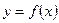 неотрицательна и непрерывна на отрезке [а, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой  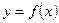на [а, b] численно равна определенному интегралу , т.е.

Пример. Найдем площадь фигуры, ограниченной линиями ,

Решение. Из рис. видно, что искомая площадь S криволинейного треугольника ОАВ равна разности двух площадей:

, '

каждая из которых находится по геометрическому смыслу определенного интеграла.

Решая систему , получаем, что точка В пересечения прямой   и кривой имеет координаты (2; 4). Тогда . Для вычисления второго интеграла определим вид подынтегральной функции, выразив из переменную у: .

Тогда получим:

 

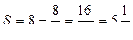Окончательно  (ед.² ).

Ответ.  ед².

Несобственные интегралы

Несобственные интегралы с бесконечными пределами интегрирования

Определение. 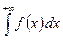 от функции f(x) на полуинтервале [a; + ¥) называется предел функции Ф(t) при t стремящемся к + ¥, т.е.

.

Если предел в правой части равенства существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

По аналогии решается вопрос в том случае, когда бесконечен нижний интервал:

При работе с несобственными интегралами решаются две основные задачи:

1) исследование вопроса о сходимости заданного несобственного интеграла;

2) вычисление значения интеграла в том случае, когда он сходится.

Использование несобственных интегралов позволяет придать вполне определенный смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры (в этом состоит геометрический смысл несобственных интегралов).

 

Несобственные интегралы от неограниченных функций

Рассмотрим случай, когда функция у=f(x) непрерывна, но не ограничена на .

Определение. Если существует и конечен предел , где d > 0, то он называется несобственным интегралом от функции от функции у=f(x) на [a; b] и обозначается 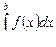, т.е. = .

В этом случае данный несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Пример. Вычислим несобственные интегралы:

1) ; 2) .

Решение.

1) Применим алгоритм вычисления несобственного интеграла с бесконечным верхним пределом. Для нахождения интеграла, находящегося под знаком предела воспользуемся формулой Ньютона-Лейбница:

2)

 Подынтегральная функция не ограничена в нижнем пределе. Применим алгоритм вычисления такого интеграла и найдем значение интеграла под знаком предела по формуле Ньютона-Лейбница:

Задание 1. Найдите рекомендуемым способом:

1)  (Раскройте скобки и проинтегрируйте почленно);

2)  (Произведите почленное деление и примените непосредственное интегрирование);

3) 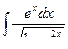 (Примите и используйте метод подстановки);

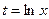4) (Примите и используйте метод подстановки);

5)  (Примите и используйте интегрирование по частям);

6)  ( Представьте подынтегральную функцию в виде

 и решите методом неопределенных коэффициентов)

7)  (Пусть , отсюда 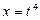 и примените метод подстановки).

(Ответ. 1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) . )

Задание 2. Вычислите интегралы:

1) ; 2) (Примените в обоих случаях метод разложения на слагаемые и непосредственное интегрирование);

3)  (Введите  и не забудьте поменять пределы интегрирования);

4) (Положите и проинтегрируйте по частям).

(Ответ. 1) 40, 2) , 3) , 4) .)

Задание 3. Выполнив построение, вычислите площадь фигуры, ограниченной линиями:

1) ;

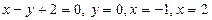2) ;

3) .

(Ответ. 1) 4 ед², 2) 36 ед², 3) 18 ед².)

Задание 4. Вычислите или установите расходимость несобственных интегралов:

1) ; 2) ; 3) .

(Ответ. 1) 0,5; 2) 0,5; 3) 1,5.)

Контрольные вопросы

1. Сформулируйте определение первообразной функции.

2. Сформулируйте определение неопределённого интеграла.

3. Сформулируйте свойства неопределённого интеграла.

4. В чём заключается геометрический смысл неопределённого интеграла.

5. Сформулируйте определение определённого интеграла.

6. Сформулируйте свойства определённого интеграла.

7. В чём заключается геометрический смысл определённого интеграла.

Контрольные задания

Вариант 1.

1. Найдите интегралы известными Вам методами:

1) ; 2) , 3) , 4) , 5) .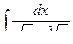

2. Вычислите известными Вам методами:

1) ; 2) ; 3) .

3. Вычислите площадь фигуры, ограниченной линиями:

1) ; 2)

Вариант 2.

1. ) ; 2) , 3) , Найдите интегралы известными Вам методами:

4) 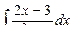, 5) .

2. Вычислите известными Вам методами:

1) 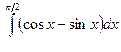; 2) ; 3) .

3. Вычислите площадь фигуры, ограниченной линиями:

1) ; 2) .

Вариант 3.

1. Найдите интегралы известными Вам методами:

1) ; 2) , 3) , 4) , 5) .

2. Вычислите известными Вам методами:

1) ; 2) ; 3) .

3. Вычислите площадь фигуры, ограниченной линиями:

1) ; 2) .

 

Сроки выполнения задания: при изучении данной темы, в течение семестра.

 

Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить все задания любого из трёх предложенных вариантов, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.

 

Самостоятельная работа № 7

«Векторы и координаты»

---

Дата добавления: 2019-01-14; просмотров: 276; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!