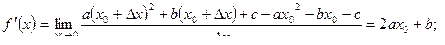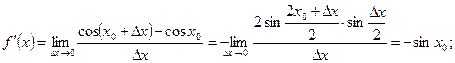Производная функции одной переменной. Правила дифференцирования. Производная сложной функции
Определение производной
Рассмотрим функцию 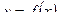 , где
, где 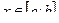 (рис. 31). Возьмем произвольную точку
(рис. 31). Возьмем произвольную точку 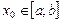 . Для любого
. Для любого 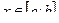 разность х – х0 называется приращением аргумента х в точке х0 и обозначается
разность х – х0 называется приращением аргумента х в точке х0 и обозначается  . Таким образом,
. Таким образом,

Разность  называется приращением функции в точке х0.
называется приращением функции в точке х0.
Определение. Производной функции  в точке х0 называется предел отношения приращения функции
в точке х0 называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при
при  , если этот предел существует и обозначается
, если этот предел существует и обозначается 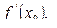
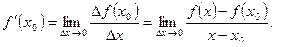
Пример. Вычислим по определению производную функции в заданной точке:
1) 
2) 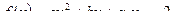
3)
| |
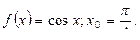
| Решение. Согласно определению производной, имеем: 1) 2) 3)
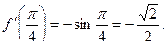
|
Ответ. 1) –3; 2) 4а + b; 3) 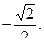
Функция, имеющая производную в точке х0, называется дифференцируемой в этой точке. Если же функция дифференцируема в каждой точке некоторого интервала  , то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
, то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция  дифференцируема в точке х0, то она непрерывна в этой точке.
дифференцируема в точке х0, то она непрерывна в этой точке.
Однако непрерывность функции в точке не является достаточным условием дифференцируемости функции в точке.
Пример. Функция 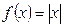 непрерывна в точке х0 = 0, но не дифференцируема в ней, поскольку
непрерывна в точке х0 = 0, но не дифференцируема в ней, поскольку 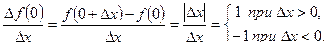
Геометрический смысл производной
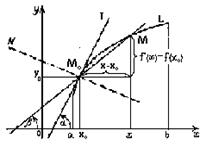
| Пусть непрерывная функция 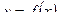 , где , где 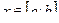 , дифференцируема в некоторой точке , дифференцируема в некоторой точке  , а кривая L – график этой функции, содержащий точку , а кривая L – график этой функции, содержащий точку  . Выберем на кривой L произвольную точку М (х; у) и построим секущую М0М (см. рис.). Точку М можно выбрать сколь угодно близко в точке М0. Положение секущей при этом будет изменяться. . Выберем на кривой L произвольную точку М (х; у) и построим секущую М0М (см. рис.). Точку М можно выбрать сколь угодно близко в точке М0. Положение секущей при этом будет изменяться.
|
Определение. Касательной к кривой L в точке М0 Î L называется прямая М0Т, занимающая предельное положение секущей М0М (М Î L) при М ® М0 (если такое положение существует).
|
|
|
Геометрический смысл производной: производная функции 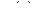 в точке х0 равна угловому коэффициенту касательной, проведенной к графику данной функции в его точке с абсциссой х0:
в точке х0 равна угловому коэффициенту касательной, проведенной к графику данной функции в его точке с абсциссой х0: 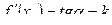 .
.
Уравнение касательной к кривой L в точке (х0; f (х0)), записанное как уравнение прямой, проходящей через точку (х0; f (х0)) и имеющей угловой коэффициент 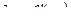 имеет вид:
имеет вид:
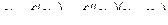
или
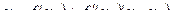 .
.
Уравнение нормали к кривой (прямой, проходящей через точку кривой L с абсциссой х0 перпендикулярно касательной) составляется аналогичным образом с учетом того, что ее угловой коэффициент равен:
 ,
то есть ,
то есть 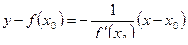 или или 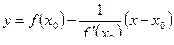 . .
|
Пример. Составим уравнения касательной и нормали к данной кривой в данной точке:
1) 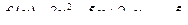
2) 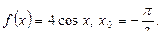
Решение.
1)
| |

Согласно определению производной, имеем: 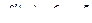
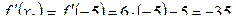
Тогда уравнение касательной примет вид: 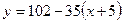 или
или 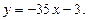
Уравнение нормали запишем в виде: 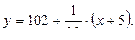
2) 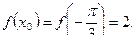
Согласно определению производной, имеем: 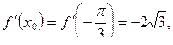
|
|
|
| |
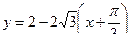 .
.
Уравнение нормали запишем в виде: 
Механический смысл производной
Положим, что материальная точка движется прямолинейно по закону 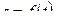 тогда ее средняя скорость за промежуток времени
тогда ее средняя скорость за промежуток времени  вычисляется по формуле:
вычисляется по формуле:

Как известно, мгновенной скоростью в момент времени t0 называется предел (если он существует), которому стремится средняя скорость за промежуток времени  при
при  , т.е.
, т.е.
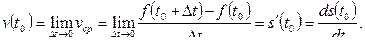
Таким образом, мгновенная скорость движения материальной точки в любой момент времени t есть производная от пути s по времени t.

В этом состоит физический смысл производной.
Пример. Найдем скорость движения материальной точки в момент времени t = 4, если закон движения задан формулой:
| |

Решение. Найдем по определению:  , тогда
, тогда 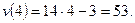
Правила дифференцирования.
Если функции u(x) и v(x) имеют производные во всех точках интервала
(a; b) , то для любого х Î (a; b) выполняются следующие равенства:
1. 
2. 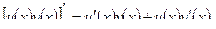
3. 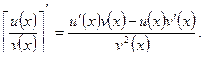
Следствие. Постоянный множитель можно выносить за знак производной:
Пример. Вычислим производные следующих функций, используя правила дифференцирования:
1. 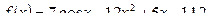
2. 
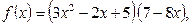
3. 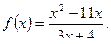
Решение. Для решения первого примера используем правило вычисления производной алгебраической суммы функций и следствие:
|
|
|
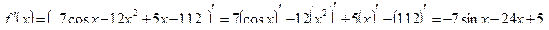
Для решения второго и третьего примеров используем правила вычисления производных произведения и отношения функций и следствие:

| |
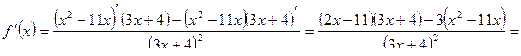
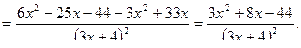
Таблица производных.
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

| C | х | хп | 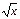
| 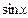
| 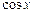
| 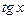
| 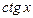
| ex | ax |
| 0 | 1 | nxn-1 | 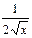
| cosx | -sin x | 
| 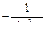
| ex | ax 
|
| № п/п | 11 | 12 | 13 | 14 | 15 | 16 |

| 
| 
| arcsinx | arccosx | arctgx | arcctgx |
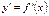
| 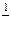
| 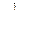
| 
| 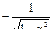
| 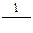
| 
|
Производная сложной и обратной функции.
С понятием сложной функции Вы уже неоднократно сталкивались в школьном курсе математики. Пусть даны две функции 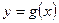 и
и 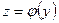 , причем область определения функции
, причем область определения функции 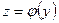 содержит область значений функции
содержит область значений функции 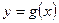 .
.
Определение. Функция, заданная формулой  , называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
, называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
Пример. Для функций 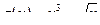 и
и 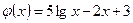 составим
составим 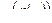 и
и 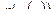 .
.
Решение.
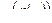  ; ;
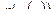 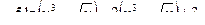 Вышеуказанный пример наглядно демонстрирует тот факт, что результат суперпозиции двух различных функций зависит от порядка, в котором эти функции следуют. Рассмотрим теорему о производной сложной функции:
Вышеуказанный пример наглядно демонстрирует тот факт, что результат суперпозиции двух различных функций зависит от порядка, в котором эти функции следуют. Рассмотрим теорему о производной сложной функции:
|
Теорема. Пусть функция 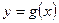 , х Î ( a; b), имеет производную в точке х0 Î ( a; b), а функция
, х Î ( a; b), имеет производную в точке х0 Î ( a; b), а функция 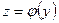 определена на интервале, содержащем множество значений функции g, и имеет производную в точке
определена на интервале, содержащем множество значений функции g, и имеет производную в точке  . Тогда сложная функция
. Тогда сложная функция 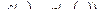 имеет производную в точке х0,, которая вычисляется по формуле:
имеет производную в точке х0,, которая вычисляется по формуле:
|
|
|

или (формулировка Лагранжа) 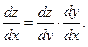
Пример. Найдем производные следующих функций:
1) 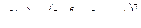 ;
;
2) 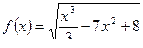 ;
;
3) 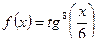 .
.
Решение.
1) Полагаем, что 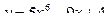 , тогда
, тогда  . Отсюда
. Отсюда
 и
и 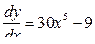 .
.
Следовательно, согласно формуле для расчета производной сложной функции, имеем:
 .
.
2) Полагаем, что  , тогда
, тогда  . Отсюда
. Отсюда
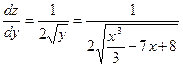 и
и 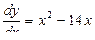 .
.
Следовательно, согласно формуле для расчета производной сложной функции, имеем:
 .
.
3) Имеем, что
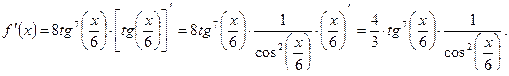
Пусть 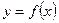 есть дифференцируемая функция от аргумента х в некотором интервале (а; b). Если в вышеуказанном уравнении у рассматривать как аргумент, а х как функцию, то последняя примет вид:
есть дифференцируемая функция от аргумента х в некотором интервале (а; b). Если в вышеуказанном уравнении у рассматривать как аргумент, а х как функцию, то последняя примет вид: 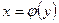 , причем
, причем 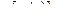 . Функция
. Функция 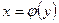 является обратной по отношению к данной и обозначается
является обратной по отношению к данной и обозначается 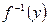 , причем
, причем 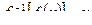 .
.
Теорема. Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е.

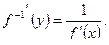
Пример. Найдем производные следующих выражений, содержащих экспоненту:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение. Произведем расчеты, используя изученные правила дифференцирования:
1) Используем формулу для расчета производной произведения и учтем, что 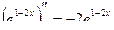 ;
; 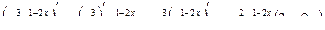 ;
;
2)  ;
;
3) 
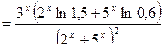 .
.
Пример. Найдем производные следующих выражений, содержащих логарифмическую функцию:
1) 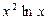 ; 2)
; 2)  ; 3)
; 3) 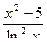 .
.
Решение.
1) 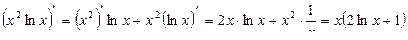 ;
;
2) Используем правило дифференцирования отношения, учитывая, что 
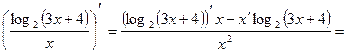
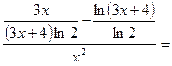
 ;
;
3) Заметим, что 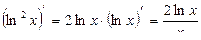 :
:
| |
 .
.
Дифференциал
Определение. Дифференциал 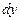 функции
функции 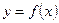 – это главная часть приращения функции
– это главная часть приращения функции 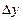 в точке х, так что
в точке х, так что  , где
, где  – бесконечно малая величина.
– бесконечно малая величина.
Дифференциал функции 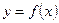 вычисляется по формуле: вычисляется по формуле:
 ,
где ,
где 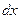 – дифференциал аргумента, равный приращению аргумента в данной точке. – дифференциал аргумента, равный приращению аргумента в данной точке.
| Запомните алгоритм вычисления дифференциала!: |
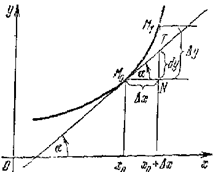
| Геометрический смысл дифференциала: дифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение  (см. рис.).
Приближенное равенство (см. рис.).
Приближенное равенство  используется в приближенных вычислениях. В таких случаях значение выражения используется в приближенных вычислениях. В таких случаях значение выражения  заменяют приближением: заменяют приближением: 
|
Пример. Вычислим приближенно  .
.
Решение. Введем функцию, выбрав в качестве значения аргумента число, позволяющее точно найти значение функции. Затем рассмотрим приращение аргумента, являющееся разностью исходного числового значения и выбранного нами (оно может быть как положительным, так и отрицательным). Вычислим дифференциал функции в данной точке и примем его приближенно равным приращению функции в этой точке. Суммируя значения функции в выбранной точке и ее приращение, получим приближенное значение исходного выражения.
Пусть 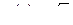 , причем
, причем 
Тогда: 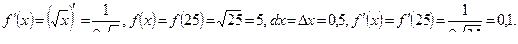
Вычислим дифференциал функции: 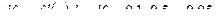 .
.
Найдем приближенное значение функции:  , то есть
, то есть  .
.
|
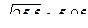 .
.
Ответ. 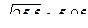 .
.
Дата добавления: 2019-01-14; просмотров: 337; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

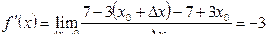 ;
;