ЗНАКИ, ЧИСЛОВЫЕ ЗНАЧЕНИЯ И СВОЙСТВА ЧЕТНОСТИ

И НЕЧЕТНОСТИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Функция y= f( x) называется четной, если при всех значениях х и области определения этой функции f( — x)= f( x).

Функция y= f( x) называется нечетной, если при всех значениях х из области определения этой функции f (—х)= — f (х).

Свойства четности и нечетности тригонометрических функций выражаются следующими формулами:

                                    sin( — α) = — sin α;                                           (8)

                                    cos(—α) = cos α;                                                 (9)

                                    tg (—α)= -tg α;                                                   (10)

                                    ctg(—α)= -ctg α.                                                 (11)

                                                                                                                          Таблица I

Четверть Функция	I 0< α <π/2	II π/2< α <π	III π< α <3π/2	IV 3π/2< α <2π
Sin α	+	+	-	-
Cos α	+	-	-	+
tg α	+	-	+	-
ctgα	+	-	+	-

 

Знаки тригонометрических функций по четвертям приведены в табл. I.

Значения тригонометрических функций некоторых дуг (углов) приведены в табл. II.

1. Какие знаки имеют: 1) cos 150°; 2) sin 320°; 3) tg.220°; 4)ctg400°?

      1) 90° < 150° < 180°    (II четверть); cos 150° <0;

      2) 270° < 320°<360°    (IV четверть); sin 320° <0;

      3) 180°<220°<270°      (III четверть); tg 220°>0;

      4) 360°<400°<360°+90° (I четверть); ctg 400°>0.

 

                                                                      Таблица II

	I четверть
	0°	30°	45°	60°	90°	180°	270°	360°
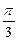
	0					π		2π
sin α	0	1/2		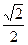	1	0	-1	0
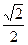
cos α	1				0	-1	0	1
tg α	0		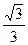1		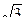Не сущ	0	Не сущ	0
Ctg α	He сущ		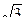1		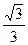0	Не сущ	0	Не сущ

 

ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА

 

  Если две функции от одних и тех же аргументов имеют одну и ту же область определения и принимают равные значения при всех допустимых значениях аргументов, то они называются тождественно равными.

  Равенство, справедливое при всех допустимых значениях аргументов, называется тождеством.

  Если в состав тождества входят тригонометрические функции, то тождество называется тригонометрическим.

Переход от данной функции к тождественно равной ей называется тождественным преобразованием функции.

При доказательстве тригонометрических тождеств обычно применяют следующие приемы:

1) производят преобразования над любой частью равенства (обычно над той, которая представляет более сложное выражение), так чтобы в результате тождественных преобразований над ней получилось выражение, стоящее в другой части равенства; 2) преобразуют одновременно обе части доказываемого тождества, пока не станет очевидным, что в обеих частях получились тождественно равные выражения; 3) используя свойство пропорции о равенстве произведений крайних и средних членов, убеждаются в равенстве этих произведений.

 

Основные тригонометрические тождества

                                               sin² α + cos² α =l;                                      (12)

                                         tg α ctg α =l. α ≠ πk/2, πk, kЄ Z;                     (13)

                                     l+tg² α =l/cos² α, α ≠π/2+ πk, kЄ Z ;                   (14)

                                         l+ctg²a= l/sin² α, α≠ πk, kЄ Z .                         (15)

   Используя основные тригонометрические тождества, можно выразить через данную тригонометрическую функцию остальные функции. Эти выражения приведены в табл. III.

                                                                                                                      Таблица III

Данная   функция	Искомая функция
	Sin α	Cos α	Tg α	Сtg α
Sin α	Sin α	±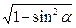
Cos α	±	Cos α
Tg α			Tg α
Сtg α		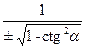		Сtg α

 

1. Дано: sin α = 3/5, π/2< α <π. Вычислить: 1) cos α; 2) tg α; 3) ctg α.

1) cos α = - = -4/5 (перед радикалом стоит минус, т.к. во II четверти cos α <0); 2) tg α = (3/5):(-4/5)=-3/4; 3) ctg α =-4/3.

2.  Дано: cos α = -12/13, π< α <3π /2. Вычислить: 1) sin α; 2) tg α; 3) ctg α.

1) sin α = -  = -5/13; 2) tg α =(-5/13):(-12/13)=5/12; 3) ctg α =12/5.

3. Дано: tg α =-3/4; π /2< α <π . Вычислить: 1) ctg α; 2) cos α; 3) sin α.

1) ctg α = - 4/3; 2) по формуле   получим cos² α = ;

cos α = - = - ; 3) sin α =  =

4. Дано: ctg α = 8/15, 0 < α <π/2. Вычислить: 1) tg α; 2) sin α; 3) cos α.

1) tg α =15/8; 2) no формуле (9.25) получим sin² α= ;

sin α = 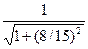= 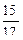;  3) cos α = =

5. Упростить выражения:

1) ; 2) sin⁴ α+ cos⁴ α +2sin² α cos² α.

1) = = = = ;

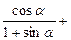
2) sin⁴ α+ cos⁴ α +2sin² α cos² α =( sin² α+ cos² α)=1²=1.

6. Доказать тождества: 1) + 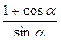= ;     2) 1 + sin α +cos α +tg α = =(l+cos α)(l+tg α); 3) =

1)( + = ) ( = ) ( = ) ( = ) ( = ),

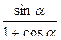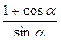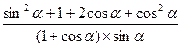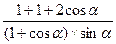2) Преобразуем левую часть:

1 +sin α +cos α + tg α = 1 +sin α + cos α + = =

= = ,

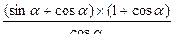Преобразуем правую часть:

(1+cos α)(1+tgα) = (1+cos α) ( ) = (1+cos α) = ,

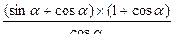Поскольку левая и правая части равны, искомое тождество доказано.

3) На основании свойства пропорции получим

(sin² α = (l - cos α)(l +cos α))  (sin² α = 1-cos² α)  (sin² α = sin² α),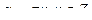

 

7. Найти значение функции:

1) y= , если tg x=2;

2) y = ,  если tg x = 3.

 

1) Так как числитель и знаменатель - однородные многочлены одной и той же степени от sin x и cos x, то их можно разделить на cos² х; тогда получим

 

y=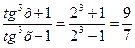

 

2) Умножив 2 в числителе и 4 в знаменателе на тригонометрическую единицу (sin²x+cos²x) и разделив затем числитель и знаменатель на cos²х, получим

 

3) y= =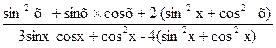

= = = =

 

 

---

Дата добавления: 2019-01-14; просмотров: 2037; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!