Односторонние пределы функции
Левосторонний предел функции.Если отыскивается предел функции f( x) при условии, что х, стремясь к а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним пределом функции f (х) (или левым пределом функции).
Для того чтобы показать, что х стремится к а, оставаясь меньше а, употребляется запись: 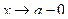 , а левосторонний предел функции обозначается символом:
, а левосторонний предел функции обозначается символом: 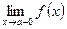 .
.
Правосторонний предел функции.Если отыскивается предел функции f( x) при условии, что х, стремясь к а, может принимать только такие значения, которые больше а, то этот предел, если он существует, называется правосторонним пределом функции f( x) (или правым пределом функции).
То, что х, стремясь к а, остается больше а, обозначается так: 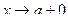 , а правосторонний предел функции обозначается символом:
, а правосторонний предел функции обозначается символом: 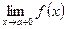 .
.
Очевидно, что предел функции при 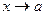 существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда
существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда 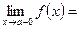
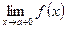 .
.
Определение Функция f( x) называется непрерывной при х = а, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т. е. f( a). То есть:
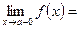
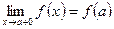 .
.
Точки разрыва и их классификация
Если равенство 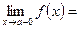
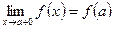 в какой-либо его части не выполняется, то о точке
в какой-либо его части не выполняется, то о точке 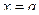 говорят, что она является точкой разрыва.
говорят, что она является точкой разрыва.
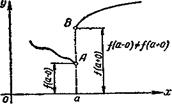
Точка разрыва первого рода
|
Определение. Если левосторонний предел функции и ее правосторонний предел существуют, но не равны, между собой, т. е. если
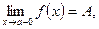 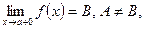 то точка а называется точкой разрыва первого рода
то точка а называется точкой разрыва первого рода
|
|
|
|
Точка разрыва второго рода
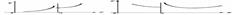 а) б) а) б)
| Определение. Если в точке х = а не существует конечный левосторонний или правосторонний предел функции или оба одновременно, то эта точка называется точкой разрыва второго рода. На рис., а отсутствует левосторонний предел функции; на рис. 3, б – нет правостороннего предела функции. |

| На рис. представлен график функции, которая не имеет в точке х = а ни левостороннего, ни правостороннего предела. Во всех этих случаях говорят, что функция в точке х = а терпит разрыв второго рода (иначе: точка х = а — точка разрыва второго рода). |
Устранимый разрыв
Определение. Если в точке х = а функция f( x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке а, т. е. со значением f( a), то точка х = а называется точкой устранимого» разрыва.
Таким образом, в этом случае 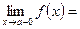
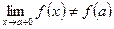 . Разрыв «устраняется» тем, что полагают
. Разрыв «устраняется» тем, что полагают 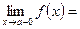
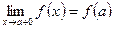 , т. е. принимают, что
, т. е. принимают, что 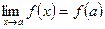 .
.
Пример. Пользуясь определением непрерывности функции через предел 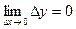 , докажем, что функция
, докажем, что функция 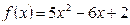 непрерывна в произвольной точке.
непрерывна в произвольной точке.
|
|
|
Решение. Выразим приращение функции при произвольном приращении аргумента в некоторой точке х:
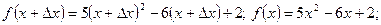
Подставим полученные выражения в формулу приращения функции, и после упрощения получим:
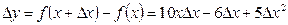 .
.
Найдем предел приращения функции при приращении аргумента, стремящемся к 0:
| |
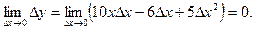
В итоге получаем, что при любом значении х предел приращения функции равен нулю, что доказывает ее непрерывность при любом значении х.
Пример. Исследуем на непрерывность при х = 1 следующую функцию:
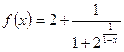 .
.
Решение. Так как знаменатель 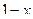 дроби равен нулю при
дроби равен нулю при 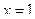 , то функция разрывна при
, то функция разрывна при 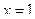 . Установим характер этой точки разрыва. Найдем сначала левосторонний предел функции:
. Установим характер этой точки разрыва. Найдем сначала левосторонний предел функции:
Если 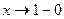 , то можно представить
, то можно представить 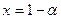 ,
, 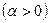 и считать, что
и считать, что 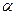 , оставаясь положительной, стремится к нулю. Заменяя х на
, оставаясь положительной, стремится к нулю. Заменяя х на 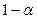 , получим:
, получим:
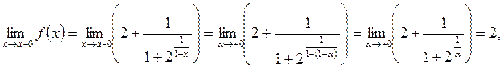
так как при 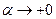 величина
величина 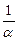 бесконечно большая,
бесконечно большая, 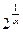 также бесконечно велика,
также бесконечно велика,  – бесконечно большая величина, обратная ей величина
– бесконечно большая величина, обратная ей величина  бесконечно мала:
бесконечно мала: 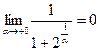 , а потому
, а потому 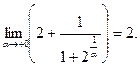
Теперь определим правосторонний предел функции. Если х →1 + 0, можно положить х = 1 + α (α > 0) и считать, что α, оставаясь положительной, стремится к нулю.
Тогда, заменяя х на 1 + α, получим:
|
|
|
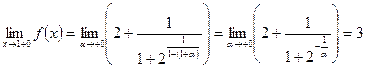 ,
,
|
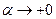 величина
величина 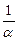 бесконечно большая,
бесконечно большая, 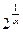 также бесконечно велика,
также бесконечно велика, 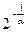 – величина бесконечно малая, т.е. ее предел будет равен 0.
– величина бесконечно малая, т.е. ее предел будет равен 0.
Итак, у функции существуют и левосторонний предел, равный 2, и правосторонний предел, равный 3, но между собой они не равны. Из этого мы заключаем, что точка 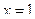 является для заданной функции точкой разрыва первого рода.
является для заданной функции точкой разрыва первого рода.
Пример. Построим графики и определим, какого рода разрыв имеет функция в данной точке (если точка не указана, определим точки разрыва самостоятельно):
1) 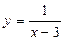 ,
, 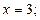 2)
2) 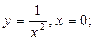 3)
3) 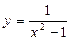 .
.
Решение.
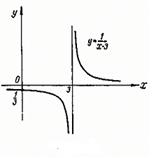
1) в точке 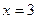 функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис., а).
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис., а).
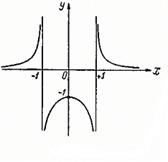
2) в точке 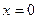 функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис., в).
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис., в).
3) функция имеет точки разрыва 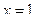 и
и 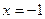 . В обеих точках функция имеет разрыв второго рода (см. рис., б).
. В обеих точках функция имеет разрыв второго рода (см. рис., б).
|
| 
| |
| а) | б) | в) |
|
| ||
Пример. Исследуем на непрерывность функцию 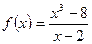 в точке х = 2.
в точке х = 2.
Решение. Так как при х = 2 функция не существует и тем самым нарушено первое условие непрерывности, то в этой точке функция терпит разрыв. Найдем левосторонний и правосторонний пределы функции:
|
|
|
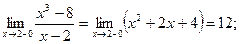
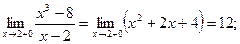

| Таким образом, существуют равные односторонние пределы данной функции в точке х = 2. Разрыв можно «устранить», если значение функции в этой точке принять равным 12, т. е. если условиться, что 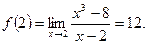 Точка х = 2 — точка «устранимого» разрыва. Графиком функции является парабола, на которой нет точки с абсциссой х = 2 (см. рис.).
Точка х = 2 — точка «устранимого» разрыва. Графиком функции является парабола, на которой нет точки с абсциссой х = 2 (см. рис.).
|
На графике эта точка обозначена кружком и к ней направлены стрелки. Сплошной ход кривой в этой точке оборвался. Слева и справа от точки х = 2 график функции — непрерывная линия.
Задание 1. Доказать, что последовательность с общим членом 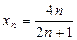 имеет предел, равный 2.
имеет предел, равный 2.
Задание 2. Пользуясь определением предела последовательности, доказать, что:
1) 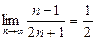
2) 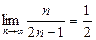
3) 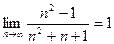
4) 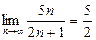
5) 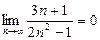
6) 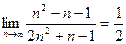
Задание 3. Найти:
1) 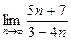
2) 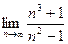
3) 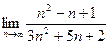
4) 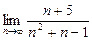
(Ответ 1) 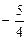 , 2) 2, 3)
, 2) 2, 3) 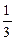 , 4) 0.)
, 4) 0.)
Задание 4. Вычислите пределы:
1) 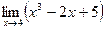 ; 2)
; 2) 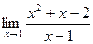 ; 3)
; 3) 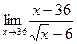 .
.
(Ответ. 1) 61, 2) 3, 3) 12.)
Задание 5. Найдите пределы 1) 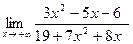 ; 2)
; 2) 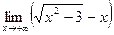 .
.
(Ответ. 1) 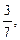 2) 0.)
2) 0.)
Задание 6. Вычислите пределы: 1) 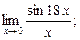 2)
2) 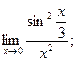 3)
3) 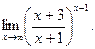
(Подсказка. В третьем задании разложите 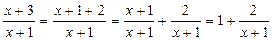 и введите новую переменную
и введите новую переменную 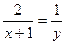 . Ответ. 1) 18, 2) 9, 3) е2.)
. Ответ. 1) 18, 2) 9, 3) е2.)
Задание 7. Исследуйте на непрерывность функции:
1) 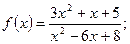 2)
2) 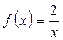 .
.
(Ответ. 1) функция непрерывна всюду, кроме значений 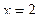 и
и 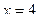 , 2) функция непрерывна всюду, кроме
, 2) функция непрерывна всюду, кроме 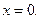 )
)
Задание 8. Пользуясь вторым определением непрерывной функции, доказать, что следующие функции непрерывны при любом значении х:
1) 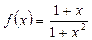 ; 2)
; 2) 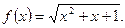
Задание 9. Испытать на непрерывность функции:
1) 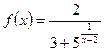 при х = 2; 2)
при х = 2; 2) 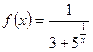 при х = 0.
при х = 0.
3) Какого рода разрыв имеет функция 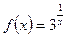 в точке х = 0. Начертить график.
в точке х = 0. Начертить график.
(Ответ. 1) точка х = 2 – точка разрыва первого рода, т.к. левосторонний и правосторонний пределы соответственно равны 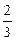 и 0; 2) х = 0 – точка разрыва первого рода; 3) разрыв второго рода.)
и 0; 2) х = 0 – точка разрыва первого рода; 3) разрыв второго рода.)
Задание 10. Исследовать на непрерывность функцию 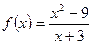 и начертить график функции. Чему должно быть равно
и начертить график функции. Чему должно быть равно 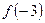 , чтобы пополненная этим значением функция была непрерывна при х = –3?
, чтобы пополненная этим значением функция была непрерывна при х = –3?
(Ответ. Точка х = –3 – точка «устранимого» разрыва. Следует взять 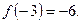 .)
.)
Вопросы для самоконтроля
- Дайте определение предела последовательности.
- Дайте определение предела функции.
- Сформулируйте теоремы о пределе функции.
- Дайте определения бесконечно малых и бесконечно больших функций.
- Назовите основные неопределенности при вычислении пределов функции.
- Объясните основные методы раскрытия неопределенностей.
- Дайте определение непрерывной функции.
- Дайте определение точек разрыва функции 1 и 2 рода.
Контрольные задания
Вариант 1.
1. Пользуясь определением предела последовательности, доказать, что 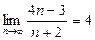 .
.
2. Найти: 1) 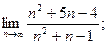 2)
2) 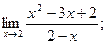 3)
3) 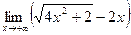 .
.
3. Вычислите при помощи первого или второго замечательных пределов: 1) 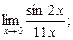 2)
2) 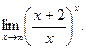
4. Исследуйте на непрерывность и определите, какого рода разрыв имеет функция: 1) 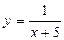 ; 2)
; 2) 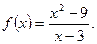
Вариант 2.
1. Пользуясь определением предела последовательности, доказать, что 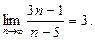 .
.
2. Найти: 1) 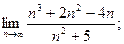 2)
2) 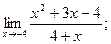 3)
3) 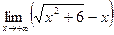 .
.
3. Вычислите при помощи первого или второго замечательных пределов: 1) 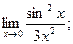 2)
2) 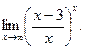
4. Исследуйте на непрерывность и определите, какого рода разрыв имеет функция: 1) 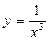 ; 2)
; 2) 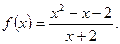
Вариант 3.
1. Пользуясь определением предела последовательности, доказать, что 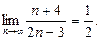 .
.
2. Найти: 1) 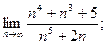 2)
2) 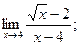 3)
3) 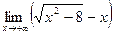 .
.
3. Вычислите при помощи первого или второго замечательных пределов: 1) 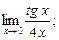 2)
2) 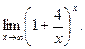
4. Исследуйте на непрерывность и определите, какого рода разрыв имеет функция: 1) 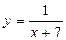 ; 2)
; 2) 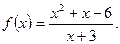
Сроки выполнения задания: при изучении данной темы, в течение семестра.
Критерии оценки задания: для получения зачёта за самостоятельную работу по данной теме необходимо выполнить все задания любого из трёх предложенных вариантов, решая задания нужно делать ссылки на используемый теоретический материал. Оформляется работа в тетради для самостоятельных работ.
Самостоятельная работа № 3
«Показательная, логарифмическая и степенная функции»
Цели:
- формирование навыков определения вида функции, нахождение её области определения;
- формирование навыков решения показательных и логарифмических уравнений и неравенств
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
ФУНКЦИЯ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И МНОЖЕСТВО ЗНАЧЕНИЙ ФУНКЦИИ
Переменная у называется функцией переменной х, если каждому допустимому значению x соответствует определенное значение у.
Символически функциональная зависимость между переменной y (функцией) и переменной х (аргументом) записывается с помощью равенства y=f(x). где f обозначает совокупность действий, которые надо произвести над .x, чтобы получить у.
Числовое значение функции, соответствующее данному числовому значению аргумента, называется частным значением этой функции. Например, функция y=f(x) при х = а принимает значение y=f(a).
Областью определения (существования) функции D(y) называется множество всех действительных значений аргумента х (множество всех точек числовой оси), при которых она имеет действительное значение.
Множеством значений функции Е(у) называется множество всех действительных значений функции у, которые она может принимать.
Для задания функции необходимо и достаточно задать закон соответствия f по которому для каждого значения аргумента можно указать единственное значение функции и область определения D(y).
Функция может быть задана аналитически (формулой), таблицей, графиком или каким-либо другим способом.
1.Дана функция: 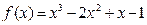 . Найти:
. Найти:  f(0), f(1), f(-1), f(2).
f(0), f(1), f(-1), f(2).
Чтобы вычислить значение f(0), надо в данную функцию вместо аргумента х подставить его значение x=0. Имеем 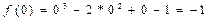 .
.
Аналогично получим 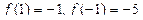 и
и 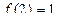
2. Найти область определения функций
1) 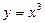 2)
2) 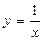 3)
3) 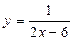 4)
4) 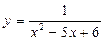
1) Здесь на х не накладывается никаких ограничений, поэтому функция у=х2 определена на множестве R.
Если х=0, то у не имеет числового значения (на нуль делить нельзя). Для всех значений (кроме нуля) у принимает действительные значения, поэтому областью определения служит вся числовая ось, кроме точки x=0.
Функция определена для всех значений х, кроме тех, при которых знаменатель дроби обращается в нуль. Решив уравнение 2х—6=0, найдем его корень х = 3. Таким образом, область определения D(y) есть вся числовая ось, кроме точки х = 3.
Функция определена для всех значений аргумента, кроме тех, при которых знаменатель обращается в нуль. Решив уравнение х2 — 5х + 6 = 0, найдем его корни: х{=2 и х2 = 3. Следовательно, область определения D(y)—вся числовая ось, кроме точек х = 2 и х = 3
3. Найти области определения функций:
1) 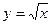 2)
2) 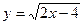 3)
3) 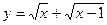 4)
4) 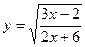
1) Квадратные корни определены для неотрицательных чисел. Поэтому функция 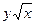 определена для всех значений ч, удовлетворяющих неравенству
определена для всех значений ч, удовлетворяющих неравенству 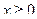 , т.е.
, т.е. 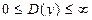
2) решив неравенство 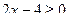 , получим
, получим 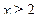 т.е.
т.е. 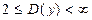
3) Найдем область определения каждого из слагаемых; общая часть этих областей и будет областью определения данной функции. Для первого слагаемого 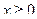 , а для второго
, а для второго 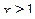 .
.
Тогда областью определения суммы 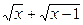 служит промежуток
служит промежуток 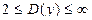
4) Функция определена для всех значений х, удовлетворяющих неравенству 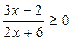 . Таким образом
. Таким образом

Следовательно областью определения функции является совокупность промежутков: 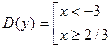
4.
- дана функция
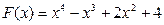 . Найдите F(0), F(-1) и F(2)
. Найдите F(0), F(-1) и F(2) - даан функция
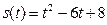 . Найдите s(0) s(2) и s(-1)
. Найдите s(0) s(2) и s(-1)
5.
1. дана функция 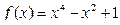 Покажите что
Покажите что 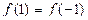
2 дана функция 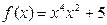 покажите что
покажите что 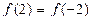
6.
1 дана функция 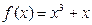 покажите что
покажите что 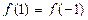
2 дана функция 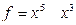 покажите что
покажите что 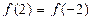
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
1. Логарифмическая функция.
Логарифмом числа N(N €€ R +) по основанию а(а>0, ≠ 1) называется показатель степени х, в которую нужно возвести основание а, чтобы получить число N, т. е.
Loga N=x 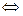 a
a 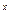 = N. (1)
= N. (1)
Равенство (1), выражающее определение логарифма, можно переписать в виде
a 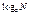 =N. (2)
=N. (2)
Это равенство называется основным логарифмическим тождеством.
Логарифмы при основании а =10 называются десятичными.
Функция 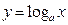 (x€R,a>0, a≠0) называется логарифмической функцией.
(x€R,a>0, a≠0) называется логарифмической функцией.
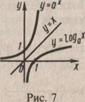
Логарифмическая функция 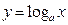 является обратной по отношению к показательной функции у=а (x€R, a>0, a≠0) Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 7).
является обратной по отношению к показательной функции у=а (x€R, a>0, a≠0) Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 7).
Приведем основные свойства логарифмической функции.
1°. Область определения: D (у) = R  .
.
2°. Множество значений функции: Е(у) = R, т.е. вся числовая прямая.
3°. Логарифм единицы равен нулю, логарифм основания равен единице: log 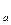 1 = 0, log
1 = 0, log 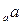 =1.
=1.
4°. Функция 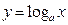 (1< а < ∞) возрастает в промежутке 0<х<∞ (рис.8). Если 1<а<∞, то log
(1< а < ∞) возрастает в промежутке 0<х<∞ (рис.8). Если 1<а<∞, то log 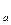 x>0 при 1<х<∞ и
x>0 при 1<х<∞ и 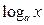 <0 при 0схс 1, т.е. при 1<а<∞ логарифмы чисел, больших единицы, положительны, а логарифмы чисел, меньших единицы, отрицательны.
<0 при 0схс 1, т.е. при 1<а<∞ логарифмы чисел, больших единицы, положительны, а логарифмы чисел, меньших единицы, отрицательны.
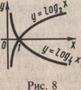
5°. Функция 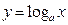 (0<а< 1) убывает в промежутке 0<х<∞ (рис. 8). Если 0<а<1, то
(0<а< 1) убывает в промежутке 0<х<∞ (рис. 8). Если 0<а<1, то 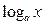 <0 при 1<х<∞ и
<0 при 1<х<∞ и 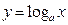 >0 при 0<х<1, т.е. при 0<а<1 логарифмы чисел, меньших единицы, положительны, а логарифмы чисел, больших единицы, отрицательны.
>0 при 0<х<1, т.е. при 0<а<1 логарифмы чисел, меньших единицы, положительны, а логарифмы чисел, больших единицы, отрицательны.
2. Алгебраические операции над логарифмами.
1°. Логарифм произведения положительных чисел равен сумме логарифмов сомножителей:
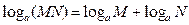 (3)
(3)
2°. Логарифм частного положительных чисел равен разности логарифмов делимого и делителя:
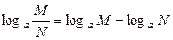 (4)
(4)
3°. Логарифм степени положительного основания равен произведению показателя степени на логарифм основания степени:
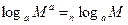 (5)
(5)
4°. Логарифм корня из положительного числа равен логарифму подкоренного числа, деленному на показатель корня:
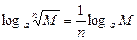 (6)
(6)
3. Логарифмирование и потенцирование.
Если число х представлено алгебраическим выражением, содержащим числа а, Ь, с, ..., то найти логарифм этого выражения — значит выразить логарифм числа х через логарифмы чисел а, Ь, с, ... . Нахождение положительного числа по его логарифму называют потенцированием.
Зависимость между логарифмами чисел при разных основаниях.
1°. Формула перехода от логарифмов по основанию а к логарифмам по основанию b
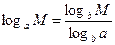 (7)
(7)
2°. Зависимость между основаниями а и b выражается формулой
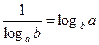 (8)
(8)
3°. Имеет место соотношение
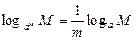
15. Найти 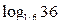 .
.
I способ. 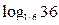 =
= 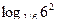 =
= 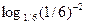 = - 2.
= - 2.
II способ. ( 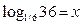 )
) 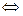 ((1 /6)
((1 /6) 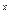 = 36)
= 36) 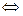 (6
(6 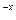 = 6
= 6 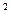 ); x=-2. •
); x=-2. •
16. Решить уравнения: l) 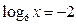 ; 2)
; 2) 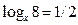 .
.
1) ( 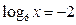 )
) 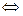 (x=6
(x=6 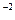 ); x=1/36
); x=1/36
2) (log 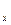 8 = - l/2)
8 = - l/2) 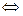 (x
(x 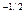 = 8)
= 8) 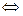 (x
(x 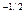 )
) 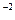 = 8
= 8 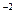 ); x=8
); x=8 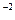 = l/64
= l/64
17. Найти области определения следующих функций:
1) 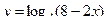 ; 2)
; 2) 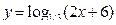 ;
;
3) 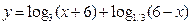
1) Здесь 8 - 2х>0, х<4, т.е. -∞ <D(у)<4.
2)Имеем 2х + 6>0, 2х>-6, х>-3, т.е. -3<D(у)<∞.
3) Имеем 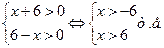
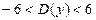
18. Построить график функции 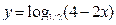
Областью определения функции служит бесконечный промежуток -∞<D(y) <2. Найдем точки пересечения графика с осями координат. Полагая у=0, получим уравнение 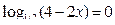 , откуда х = 3/2. При х = 0 имеем
, откуда х = 3/2. При х = 0 имеем 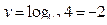 . График функции изображен на рис. 9. ●
. График функции изображен на рис. 9. ●
Дата добавления: 2019-01-14; просмотров: 2101; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!