Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• перестановка местами двух параллельных рядов матрицы;

• умножение всех элементов ряда матрицы на число, отличное от нуля;

• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же чи­сло.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразова­ний. Записывается А-В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят под­ряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

 

Пример 1.4.Привести к каноническому виду матрицу

 

A =

Решение: Выполняя элементарные преобразования, получаем

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А _{m x n} = (a_ij) на матрицу В_{т xp} - ( b_jk ) называется матрица С_тхр = (c_ik) такая, что

c_ik = a_i1 • b_1k + a_i2 • b_2k + … + a_in • b_nk , где i = , k= ,

т. е. элемент i-й строки и k-го столбца матрицы произведения С равен cумме произведений элементов i-й строки матрицы А на соответству­ющие элементы k-го столбца матрицы В.

Получение элемента с_ik схематично изображается так:

Если матрицы А и В квадратные одного размера, то произведения АВ и В А всегда существуют. Легко показать, что А • Е = Е • А = А, где А — квадратная матрица, Е — единичная матрица того же размера.

Пример:

 _2×3 ×  _3×2 = 

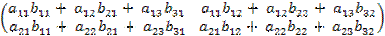=  _2×2

Пример:

A = , B =

Тогда изображение А-В не определено, так как число столбцов матрицы А(3) не совпада­ет с числом строк матрицы В(2). При этом определено произведение В х А, которое считают следующим образом:

B • A =  •  =  =

Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:

1. А • (В • С) = (А • В) • С;

2. А(В + С) = АВ + АС;

3. (А + В) • С = АС + ВС;

4. α(АВ) т (αА)В,

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

1. (А + В)^Т = А^Т + В^Т;

2. (АВ)^Т = В^Т • А^Т.

ОПРЕДЕЛИТЕЛИ

Основные понятия

Квадратной матрице А порядка n можно сопоставить число detA (или , или Δ), называемое ее определителем, следующим образом:

 

1. n = 1. A =  ; det A =

2. n = 2. A =  ; det A =  =  •

3. n = 3, A = 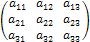 ; det A =  =

=

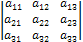Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N являет­ся довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некото­рого ряда (с. 23, свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

Пример 2.1. Найти определители матриц

  и

Решение:

 = 2 • 6 – 5 • (-3) = 12 – (-15) = 27;

 = cos²α + sin²α = 1

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример 2.2. Вычислить определитель матрицы

A =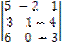

Решение:

det А = 5•1(-3) + (-2) • (-4) •6 + 3•0•1 - 6•1•1 - 3•(-2)•(-3) - 0•(-4) •5 = -15 + 48 - 6 - 18 = 48 - 39 = 9.

 

Свойства определителей

Сформулируем основные свойства определителей, присущие опре­делителям всех порядков. Некоторые из этих свойств поясним на опре­делителях 3-го порядка.

Свойство 1(«Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.

Иными словами,

 

 = ,  =

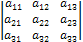В дальнейшем строки и столбцы будем просто называть рядами опре­делителя.

Свойство 2. При перестановке двух параллельных рядов опреде­литель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда опре­делителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

 = k• 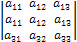 = k•0 = 0

Свойство 5. Если элементы какого-либо ряда определителя пред­ставляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

 =  =

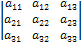Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

Пример 2.3. Доказать, что

 

∆ =  =

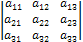Решение: Действительно, используя свойства 5, 4 и 3, получим

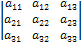 =  + k• 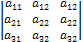 = ∆ + k•0 = ∆

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Миноромнекоторого элемента а_ij определителя n-го порядка на­зывается определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых нахо­дится выбранный элемент. Обозначается m_ij.

Так, если

 

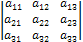∆ = , то ,

Алгебраическим дополнениемэлемента a_ij определителя на­зывается его минор, взятый со знаком «плюс», если сумма i+ j — четное число, и со знаком «минус», если эта сумма нечетная. Обозна­чается A_ij; A_ij = (-1)^i+j • m_ij.

Так, A₁₁ = +m₁₁, A₃₂ = -m₃₂.

Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

 

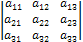∆ =  = α₁₁ • A₁₁ + α₁₂ • A₁₂ + α₁₃ • A₁₃

В самом деле, имеем

a₁₁ • A₁₁ + a₁₂ • А₁₂ + а₁₃ • A₁₃ = α₁₁ •  + α₁₂ •  + α₁₃ •  =

= α₁₁(α₂₂ α33 – α₂₃ α₃₂) - α₁₂(α₂₁ α₃₃ – α₂₃ α₃₁) + α₁₃(α₂₁ α₃₂ – α₂₂ α₃₁) =

= α₁₁ α₂₂ α₃₃ - α₁₁ α₂₃ α₃₂ - α₁₂ α₂₁ α₃₃ + α₁₂ α₂₃ α₃₁ + α₁₃ α₂₁ α₃₂ - α₁₃ α₂₂ α₃₁ = ∆

Свойство 7 содержит в себе способ вычисления определителей вы­соких порядков.

Пример 2.4 .Вычислите определитель матрицы

 

 

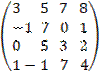
Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в раз­ложении будут равны нулю.

 

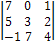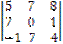 = 3•  + 1•  + 0•  - 1•  =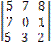

= 3•(7•3•4 + (-1) •0•2 + 5•7•1 – (-1) •3•1 - 7•7•2 - 5•0•4) + (5•3•4 + (-1) •7•2 + 5•7•8 – (-1) • 3•8 –

- 5•7•4 - 5•7•2) – (5•0•2 + 7•1•5 + 7•3•8 - 5•0•8 - 3•1•5 -7•7•2) = 122

Свойство 8. Сумма произведений элементов какого-либо ряда оп­ределителя на алгебраические дополнения соответствующих элемен­тов параллельного ряда раина нулю.

Так, например, a₁₁А₂₁+a₁₂A₂₂+а₁₃А₂₃= 0.

НЕВЫРОЖДЕННЫЕ МАТРИЦЫ.

Основные понятия

Пусть А — квадратная матрица n-го порядка

 

A =

 

Квадратная матрица A называется невырожденной, если опре­делитель Δ = detA не равен нулю: Δ = detA≠0. В противном случае (Δ = 0) матрица А называется вырожденной.

Матрицей, союзной к матрице A , называется матрица

 

A* =

где A_ij — алгебраическое дополнение элемента a_ij данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента

определителя).

Матрица А^-1 называется обратной матрице А, если выполняется условие

A•A^-1=A^-1•A = Е,                                               (3.1)

где Е — единичная матрица того же порядка, что и матрица А. Матрица А имеет те же размеры, что и матрица А.

 

Обратная матрица

 

Теорема 3.1. Всякая невырожденная матрица имеет обратную.

Проведем доказательство для случая матрицы 3-го порядка. Пусть

A =  , причём det A ≠ 0

Составим союзную матрицу

A* =

и найдем произведение матриц Aи A^*:

 

A • A* =  •  =

=  =

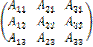=  = det A  = det A • E;

т.е. A • A* = det A•E

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

A^*•A = detA•E.                                                               (3.3)

Равенства (3.2) и (3.3) перепишем в виде

 

A^-1 =  , т.е. A^-1 =  •

Отметим свойства обратной матрицы:

1. det(A^-1) =  ;

2. (A • B)^-1 = B^-1 • A^-1 ;

3. (A^-1)^T = (A^T)^-1

Пример 3.1. Найти А¹, если А =

Решение: 1) Находим detA:

 

det A =  = 2+3 = 5 ≠ 0

2) Находим А^*: А₁₁=1, А₂₁=-3, A_l2=-(-1)=1, A₂₂=2, поэтому

 

A* =

3) Находим A^-1:

 

A^-1 =  =

Проверка:

 

A • A^-1 =  •  =  =  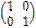= E

 

Пример 3.2. Определить, при каких значениях А существует ма­трица, обратная данной:

 

A =

Решение: Всякая невырожденная матрица имеет обратную. Найдем определитель матрицы А:

 

∆A =  = 3-0+2ℷ-12-0+2ℷ = 4ℷ - 9

Если 4λ – 9 ≠ 0, т. е. λ ≠ , то ΔA ≠0, т. е. матрица А невырожденная, имеет обратную.

Пример 3.3. Показать, что матрица А является обратной для В, если

 

A = , B =

Решение: Найдем произведение матриц A и В:

 

A • B =  •

=  =  = E

Аналогично В • A = Е. Следовательно, матрица А является обратной дня В.

 

Ранг матрицы

Рассмотрим матрицу А размера m х n.

 

 

Выделим и ней k прок и k столбцов (k ≤ min(m;n)). Из элемен­тов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются ми­норами этой матрицы. В матрице A пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить  •  штук, где  =  - число сочетаний из n элементов по k.)

Наибольший из порядков миноров данной матрицы. отличных от нуля, называется рангомматрицы. Обозначается r, r(A) иди rang А.

Очевидно, что 0≤r≤min(m; n), где min(m; n) — меньшее из чисел m и n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример 3.4. Найти ранг матрицы:

 

A =

Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля

 = -15 ≠ 0. Значит, r(A) = 2. Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.

Отметим свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Ранг канонической матрицы равен числу единиц на главной диа­гонали. На этом основан одни из способов вычисления ранга матрицы.

Пример 3.5.Найти ранг матрицы

 

A =

 

используя результаты примера 1.4.

Решение: В примере 1.4 показано,

 

A ~

то есть

 

A ~

Таким образом, ранг матрицы Aравен r(A) = 2.

 

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Основные понятия

Системой линейных алгебраических уравнений, содержащей m уравнений и п неизвестных, называется система вида

 

где числа a_ij, i = , j =  называются коэффициентами системы, числа b_i — свободными членами. Подлежат нахождению числа x_n.

Такую систему удобно записывать в компактной матричной форме

 

A • X = B

Здесь А — матрица коэффициентов системы, называемая основной матрицей:

 

A =

 

X =   - вектор-столбец из неизвестных ,

B = 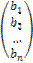   - вектор-столбец из свободных членов

Произведение матриц A•X определено, так как в матрице Aстолб­цов столько же, сколько строк в матрице X (п штук).

Расширенной матрицей системы называется матрица А системы, дополненная столбцом свободных членов

 

=

 

Решением системы называется п значений неизвестных х₁ = c₁, x₂ = c₂, ..., х_n= с_n, при подстановке которых все уравнения системы обраща­ются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца

 

C =

Система уравнений называется совместной, если она имеет, хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему — это значит выяснить, совместна она или не­совместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементар­ных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной, если все сво­бодные члены равны нулю:

 

 

Однородная система всегда совместна, так как х₁ = х₂ = • • • = х_n = 0 является решением системы. Это решение называется нулевым или тривиальным.

---

Дата добавления: 2019-01-14; просмотров: 1723; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!