Рекомендации по конспектированию

Конспект — сложная запись содержания исходного текста, включающая в себя заимствования (цитаты) наиболее примечательных мест в соответствии с планом источника, а также сжатый анализ записанного материала и выводы по нему.

Общий порядок работы над конспектом:

¾ определение структуры конспектируемого материала, при этом очень помогает составление плана по ходу изучения текста;

¾ отбор и последующая запись наиболее существенного содержания текста в форме цитат, доказательств или близкого изложения без потерь смысла;

¾ анализ записей и на его основе дополнение наиболее сложных элементов текста;

¾ комментарии (располагать их можно на полях или в виде сносок);

¾ завершение формулирования и запись выводов по каждой из частей текста, а также общих выводов в заключении.

Самостоятельная работа № 1

«Действительные числа»

 

Цели:

– формирование навыков выполнения действий над матрицами;

– формирование навыков решения систем линейных уравнений различными методами

 

МАТРИЦЫ

Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая т строк одинаковой длины (или n столбцов одинаковой длины). Ма­трица записывается в виде

 

 

 

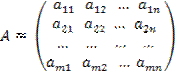
или, сокращенно, А = (а_ij), где i = 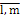 (т. е. i = 1,2,3,.. .,m) — номер строки, j = 1,n (т. е. j = 1,2,3,..., п) — номер столбца.

Матрицу A называют матрицей размера m x n и пишут А _{m x n} - Чи­сла a_ij , составляющие матрицу, называются ее элементами. Элемен­ты, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Ј5j Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.

А = В, если aij = 6,j, где i = l,m, j = X ,п.. Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера пхп называют матрицей п-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диаго­нали равен единице, называется единичной. Обозначается буквой Е.

Пример 1.1.

 

E_3×3 =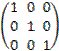

— единичная матрица 3-го порядка.

 

E_n×n =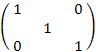

— единичная матрица n-ro порядка.

· Квадратная матрица называется треугольной, если все элемен­ты, расположенные по одну сторону от главной диагонали, равны нулю.

· Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Имеет вид

 

O =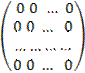

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.

· Матрица, содержащая один столбец или одну строку, называется вектором(или вектор-столбец, или вектор-строка соответствен­но). Их вид:

 

A = 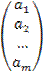, B =

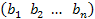
Матрица размера 1x1, состоящая из одного числа, отождествля­ется с этим числом, т. е. (5)_1х1 есть 5.

· Матрица, полученная из данной заменой каждой ее строки столб­цом с тем же номером, называется матрицей транспонирован­нойк данной. Обозначается A^T .

 

Так, если A = 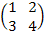, то A^T  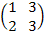= , если A = , то A^T =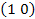

Транспонированная матрица обладает следующим свойством: (А^Т)^Т = А.

Действия над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинако­вых размеров.

Суммой двух матриц А _{m x n} = (а_jj) и В_тхп = ( b_ij ) называется матрица С_тхп = (с_ij) такая, что с_ij = а_jj + b_ij (i =
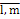, j = ).

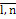Пример 1.2.

 

 +  =

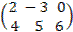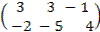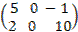
Аналогично определяется разность матриц.

Умножение на число

Произведением матрицы А _{m x n} = (а_ij) на число kназывается ма­трица В_{т x п} = ( b_ij ) такая, что b_ij = k • а_ij (i = 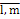, j = ).

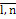Пример 1.3.

 

A = 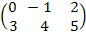 , k = 2, A  k =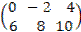

Матрица -А = (-1) • А называется противоположной матрице А.

Разность матриц А - В можно определить так: А - В — А + (—В). Операции сложения матриц и умножения матрицы на число обла­дают следующими свойствами:

1. А + В = В + А;

2. А + (В + С) = (А + В) + С;

3. А + 0 = А;

4. А-А = 0;

5. 1-А = А;

6. α • (A + В) = αА + βВ;

7. (α + β) •А = αА+βА;

8. а • (βА) = (αβ) • А,

где А, В, С ~ матрицы, α и β— числа.

 

---

Дата добавления: 2019-01-14; просмотров: 333; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!